Giải bài 41 trang 77 SBT Toán 12 Cánh Diều

Giải bài 41 trang 77 sách bài tập toán 12 - Cánh diều

Tusach.vn xin giới thiệu đáp án chi tiết bài 41 trang 77 sách bài tập Toán 12 Cánh Diều. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Chúng tôi luôn cập nhật nhanh chóng và chính xác các bài giải SBT Toán 12 Cánh Diều, hỗ trợ tối đa cho quá trình học tập của bạn.

Cho hình lập phương (ABCD.A'B'C'D') có cạnh bằng (a). Tính: a) (overrightarrow {A'B} .overrightarrow {B'C'} ); b) (overrightarrow {D'A} .overrightarrow {BA'} ).

Đề bài

Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Tính:

a) \(\overrightarrow {A'B} .\overrightarrow {B'C'} \);

b) \(\overrightarrow {D'A} .\overrightarrow {BA'} \).

Phương pháp giải - Xem chi tiết Giải bài 41 trang 77 sách bài tập toán 12 - Cánh diều 1

Sử dụng tích vô hướng của hai vectơ: \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\).

Lời giải chi tiết

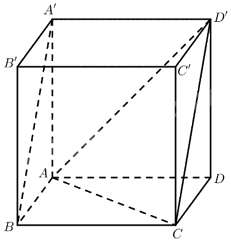
Giải bài 41 trang 77 sách bài tập toán 12 - Cánh diều 2

a) Ta có: \(B'C' \bot \left( {ABB'A'} \right) \Rightarrow B'C' \bot A'B\).

\( \Rightarrow \left( {\overrightarrow {A'B} ,\overrightarrow {B'C'} } \right) = {90^ \circ } \Rightarrow \overrightarrow {A'B} .\overrightarrow {B'C'} = 0\)

b) Ta có:

\(\overrightarrow {D'A} .\overrightarrow {BA'} = - \overrightarrow {D'A} .\overrightarrow {A'B} = - \left| {\overrightarrow {D'A} } \right|.\left| {\overrightarrow {A'B} } \right|.\cos \left( {\overrightarrow {D'A} ,\overrightarrow {A'B} } \right) = - AD'.A'B.\cos \left( {\overrightarrow {D'A} ,\overrightarrow {A'B} } \right)\)

\(\overrightarrow {A'B} = \overrightarrow {D'C} \Rightarrow \left( {\overrightarrow {D'A} ,\overrightarrow {A'B} } \right) = \left( {\overrightarrow {D'A} ,\overrightarrow {D'C} } \right) = \widehat {A{\rm{D}}'C}\).

Xét tam giác \(AC{\rm{D}}'\) có \(AC,AD',CD'\) đều là các đường chéo của các hình vuông là các mặt của hình lập phương.

Do đó \(AC = AD' = CD'\). Vậy tam giác \(AC{\rm{D}}'\) đều.

Suy ra \(\left( {\overrightarrow {D'A} ,\overrightarrow {A'B} } \right) = \widehat {A{\rm{D}}'C} = {60^ \circ }\).

\(\overrightarrow {D'A} .\overrightarrow {BA'} = - a.a.\cos {60^ \circ } = - \frac{{{a^2}}}{2}\).

Giải bài 41 trang 77 SBT Toán 12 Cánh Diều: Tổng quan và Phương pháp giải

Bài 41 trang 77 sách bài tập Toán 12 Cánh Diều thuộc chương trình học Toán 12, tập trung vào kiến thức về Đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về:

Vị trí tương đối giữa đường thẳng và mặt phẳng: Xác định đường thẳng song song, nằm trong, cắt hoặc vuông góc với mặt phẳng.
Góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
Khoảng cách từ một điểm đến mặt phẳng: Tính khoảng cách từ một điểm đến mặt phẳng sử dụng công thức hoặc phương pháp tọa độ.

Đáp án chi tiết bài 41 trang 77 SBT Toán 12 Cánh Diều

Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, Tusach.vn xin trình bày đáp án chi tiết như sau:

Câu a: (Ví dụ minh họa - cần thay thế bằng nội dung bài toán thực tế)

Đề bài: Cho đường thẳng d và mặt phẳng (P). Xác định vị trí tương đối giữa d và (P).

Giải: Để xác định vị trí tương đối giữa đường thẳng d và mặt phẳng (P), ta cần tìm giao điểm của d và (P). Nếu d và (P) có một điểm chung, thì d cắt (P). Nếu d và (P) không có điểm chung, thì d song song với (P). Để tìm giao điểm, ta giải hệ phương trình gồm phương trình đường thẳng d và phương trình mặt phẳng (P)....

Câu b: (Ví dụ minh họa - cần thay thế bằng nội dung bài toán thực tế)

Đề bài: Tính góc giữa đường thẳng d và mặt phẳng (P).

Giải: Góc giữa đường thẳng d và mặt phẳng (P) là góc giữa đường thẳng d và hình chiếu của nó trên mặt phẳng (P). Để tính góc này, ta sử dụng công thức: sin(α) = d(A, (P)) / AD, trong đó A là một điểm bất kỳ trên đường thẳng d, d(A, (P)) là khoảng cách từ A đến mặt phẳng (P), và AD là độ dài đoạn thẳng AD...

Mẹo giải bài tập về Đường thẳng và mặt phẳng trong không gian

Để giải tốt các bài tập về đường thẳng và mặt phẳng trong không gian, các em cần nắm vững các kiến thức cơ bản sau:

Nắm vững định nghĩa và tính chất của các yếu tố hình học: Đường thẳng, mặt phẳng, góc, khoảng cách,...
Sử dụng thành thạo các phương pháp tọa độ: Phương pháp tọa độ giúp giải quyết các bài toán một cách dễ dàng và chính xác.
Rèn luyện kỹ năng hình dung không gian: Kỹ năng hình dung không gian giúp các em hiểu rõ hơn về mối quan hệ giữa các yếu tố hình học.
Luyện tập thường xuyên: Luyện tập thường xuyên giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Tusach.vn – Đồng hành cùng bạn trên con đường chinh phục môn Toán

Tusach.vn là website chuyên cung cấp đáp án và lời giải chi tiết các bài tập trong sách giáo khoa và sách bài tập Toán 12. Chúng tôi cam kết cung cấp nội dung chính xác, dễ hiểu và cập nhật nhanh chóng. Hãy truy cập Tusach.vn để được hỗ trợ tốt nhất trong quá trình học tập!

Chương	Bài	Trang
Đường thẳng và mặt phẳng trong không gian	41	77