Giải bài 20 trang 14 sách bài tập toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 20 trang 14 SBT Toán 12 Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 20 trang 14 sách bài tập Toán 12 Cánh Diều. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 12 Cánh Diều, đáp ứng nhu cầu học tập của học sinh.
Tìm điểm cực trị của mỗi hàm số sau: a) \(y = {x^3} - 12{\rm{x}} + 8\); b) \(y = 2{{\rm{x}}^4} - 4{{\rm{x}}^2} - 1\); c) \(y = \frac{{{x^2} - 2{\rm{x}} - 2}}{{x + 1}}\); d) \(y = - x + 1 - \frac{9}{{x - 2}}\)
Đề bài
Tìm điểm cực trị của mỗi hàm số sau:
a) \(y = {x^3} - 12{\rm{x}} + 8\); b) \(y = 2{{\rm{x}}^4} - 4{{\rm{x}}^2} - 1\);
c) \(y = \frac{{{x^2} - 2{\rm{x}} - 2}}{{x + 1}}\); d) \(y = - x + 1 - \frac{9}{{x - 2}}\)
Phương pháp giải - Xem chi tiết
Các bước để tìm điểm cực trị của hàm số \(f\left( x \right)\):
Bước 1. Tìm tập xác định của hàm số \(f\left( x \right)\).
Bước 2. Tính đạo hàm \(f'\left( x \right)\). Tìm các điểm \({x_i}\left( {i = 1,2,...,n} \right)\) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.
Bước 3. Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4. Căn cứ vào bảng biến thiên, nêu kết luận về các điểm cực trị của hàm số.
Lời giải chi tiết
a) Hàm số có tập xác định là \(\mathbb{R}\).
Ta có: \({y^\prime } = 3{{\rm{x}}^2} - 12\); \(y' = 0\) khi \(x = - 2,x = 2\).
Bảng biến thiên của hàm số:
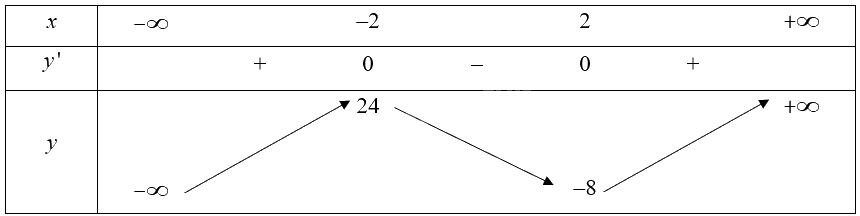
Vậy hàm số đạt cực tiểu tại \(x = 2\) và đạt cực đại tại \(x = - 2\).
b) Hàm số có tập xác định là \(\mathbb{R}\).
Ta có: \({y^\prime } = 8{{\rm{x}}^3} - 8{\rm{x}}\)
\(y' = 0\) khi \(x = 0,x = - 1,x = 1\).
Bảng biến thiên của hàm số:
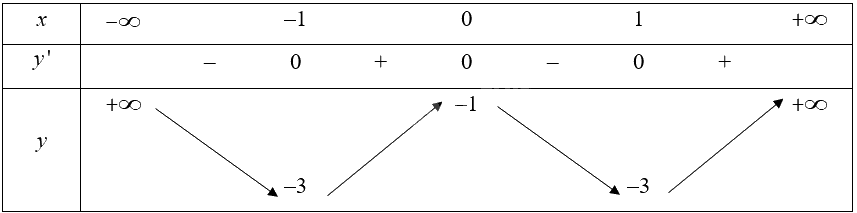
Vậy hàm số đạt cực tiểu tại \(x = - 1\) và \(x = 1\), đạt cực đại tại \(x = 0\).
c) Hàm số có tập xác định là \(\mathbb{R}\backslash \left\{ { - 1} \right\}\).
Ta có:
\(\begin{array}{l}{y^\prime } = \frac{{{{\left( {{x^2} - 2x - 2} \right)}^\prime }.\left( {x + 1} \right) - \left( {{x^2} - 2x - 2} \right).{{\left( {x + 1} \right)}^\prime }}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{\left( {2{\rm{x}} - 2} \right)\left( {x + 1} \right) - \left( {{x^2} - 2x - 2} \right)}}{{{{\left( {x + 1} \right)}^2}}}\\ & = \frac{{{x^2} + 2{\rm{x}}}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{x\left( {{\rm{x}} + 2} \right)}}{{{{\left( {x + 1} \right)}^2}}}\end{array}\)
\(y' = 0\) khi \(x = 0,x = - 2\).
Bảng biến thiên của hàm số:
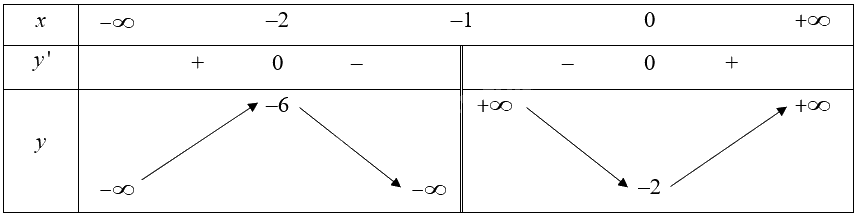
Vậy hàm số đạt cực tiểu tại \(x = 0\) và đạt cực đại tại \(x = - 2\).
d) Hàm số có tập xác định là \(\mathbb{R}\backslash \left\{ 2 \right\}\).
Ta có:
\({y^\prime } = - 1 + \frac{9}{{{{\left( {x - 2} \right)}^2}}} = \frac{{ - {x^2} + 4{\rm{x}} - 4 + 9}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{ - {x^2} + 4{\rm{x}} + 5}}{{{{\left( {x - 2} \right)}^2}}}\)
\(y' = 0\) khi \(x = 5,x = - 1\).
Bảng biến thiên của hàm số:
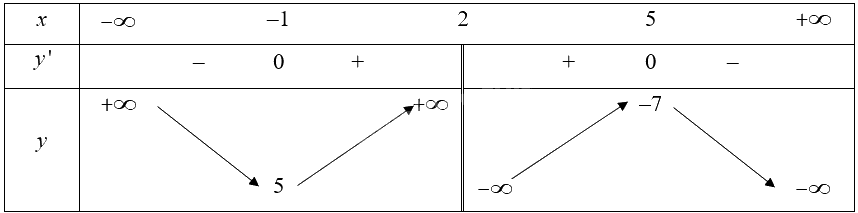
Vậy hàm số đạt cực tiểu tại \(x = - 1\) và đạt cực đại tại \(x = 5\).
Giải bài 20 trang 14 SBT Toán 12 Cánh Diều: Tổng quan và Phương pháp giải
Bài 20 trang 14 sách bài tập Toán 12 Cánh Diều thuộc chương trình học Toán 12, tập trung vào kiến thức về đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về vectơ, phương trình đường thẳng, phương trình mặt phẳng để giải quyết các bài toán liên quan đến quan hệ vị trí giữa đường thẳng và mặt phẳng.
Nội dung chi tiết bài 20 trang 14 SBT Toán 12 Cánh Diều
Bài 20 thường bao gồm các dạng bài tập sau:
- Xác định vị trí tương đối giữa đường thẳng và mặt phẳng: Bài tập này yêu cầu học sinh xác định xem một đường thẳng có nằm trong, song song hoặc cắt một mặt phẳng hay không.
- Tìm giao điểm của đường thẳng và mặt phẳng: Học sinh cần tìm tọa độ giao điểm của đường thẳng và mặt phẳng nếu chúng cắt nhau.
- Tính góc giữa đường thẳng và mặt phẳng: Bài tập này yêu cầu học sinh tính góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
- Tìm hình chiếu của đường thẳng lên mặt phẳng: Học sinh cần xác định phương trình đường thẳng là hình chiếu của đường thẳng đã cho lên mặt phẳng.
Hướng dẫn giải bài 20 trang 14 SBT Toán 12 Cánh Diều
Để giải quyết các bài tập trong bài 20 trang 14 SBT Toán 12 Cánh Diều một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
- Vectơ chỉ phương của đường thẳng và vectơ pháp tuyến của mặt phẳng: Hiểu rõ cách xác định và sử dụng các vectơ này để xác định quan hệ vị trí giữa đường thẳng và mặt phẳng.
- Phương trình đường thẳng và phương trình mặt phẳng: Nắm vững các dạng phương trình của đường thẳng và mặt phẳng, cũng như cách chuyển đổi giữa các dạng phương trình khác nhau.
- Điều kiện đồng phẳng của ba vectơ: Sử dụng điều kiện đồng phẳng để xác định xem ba vectơ có cùng nằm trên một mặt phẳng hay không.
- Công thức tính khoảng cách từ một điểm đến một mặt phẳng: Áp dụng công thức này để tính khoảng cách từ một điểm đến một mặt phẳng.
Ví dụ minh họa giải bài 20 trang 14 SBT Toán 12 Cánh Diều
Ví dụ: Cho đường thẳng d: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P): 2x - y + z - 5 = 0. Xác định vị trí tương đối giữa đường thẳng d và mặt phẳng (P).
Giải:
Vectơ chỉ phương của đường thẳng d là a = (1, -1, 2). Vectơ pháp tuyến của mặt phẳng (P) là n = (2, -1, 1).
Ta có a.n = 1*2 + (-1)*(-1) + 2*1 = 5 ≠ 0. Do đó, đường thẳng d và mặt phẳng (P) cắt nhau.
Lưu ý khi giải bài tập
- Luôn kiểm tra lại các phép tính và kết quả để đảm bảo tính chính xác.
- Sử dụng các công thức và định lý một cách chính xác.
- Rèn luyện kỹ năng giải toán thường xuyên để nâng cao khả năng giải quyết các bài tập khó.
Tusach.vn – Đồng hành cùng bạn học Toán 12
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách bài tập Toán 12 Cánh Diều. Chúng tôi hy vọng rằng với sự hỗ trợ của Tusach.vn, các bạn học sinh sẽ học tập hiệu quả và đạt kết quả tốt trong môn Toán.
| Bài tập | Lời giải |
|---|---|
| Bài 1 | Xem lời giải |
| Bài 2 | Xem lời giải |