Giải bài 55 trang 24 SBT Toán 12 Cánh Diều

Giải bài 55 trang 24 sách bài tập toán 12 - Cánh diều

Tusach.vn xin giới thiệu đáp án chi tiết bài 55 trang 24 sách bài tập Toán 12 Cánh Diều. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Chúng tôi luôn cập nhật nhanh chóng và chính xác các bài giải SBT Toán 12 Cánh Diều, hỗ trợ tối đa cho quá trình học tập của bạn.

Cho hàm số (y = fleft( x right)) xác định trên (mathbb{R}backslash left{ { - 2} right}), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: Khẳng định nào sau đây là đúng? A. Đồ thị hàm số có tiệm cận đứng là đường thẳng (x = - 2) và không có tiệm cận ngang. B. Đồ thị hàm số có tiệm cận đứng là đường thẳng (x = - 2) và tiệm cận ngang là đường thẳng (y = 3). C. Đồ thị hàm số không có tiệm cận đứng và tiệm cận ngang là đường thẳng (y = - 2). D. Đồ thị hàm

Đề bài

Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ { - 2} \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

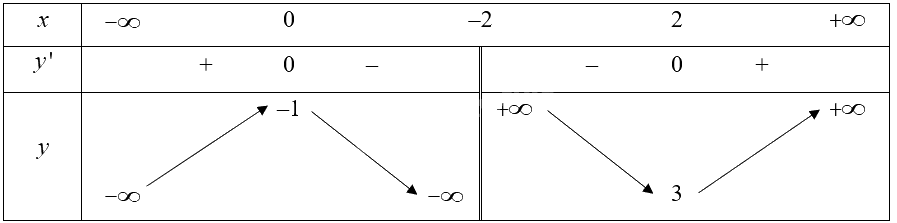
Giải bài 55 trang 24 sách bài tập toán 12 - Cánh diều 1

Khẳng định nào sau đây là đúng?

A. Đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = - 2\) và không có tiệm cận ngang.

B. Đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = - 2\) và tiệm cận ngang là đường thẳng \(y = 3\).

C. Đồ thị hàm số không có tiệm cận đứng và tiệm cận ngang là đường thẳng \(y = - 2\).

D. Đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = - 2\) và tiệm cận ngang là đường thẳng \(y = 3\).

Phương pháp giải - Xem chi tiết Giải bài 55 trang 24 sách bài tập toán 12 - Cánh diều 2

‒ Tìm tiệm cận đứng: Tính \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right)\) hoặc \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right)\), nếu một trong các giới hạn sau thoả mãn: \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = - \infty ;\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = - \infty \)

thì đường thẳng \(x = {x_0}\) là đường tiệm cận đứng.

‒ Tìm tiệm cận ngang: Nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\) thì đường thẳng \(y = {y_0}\) là đường tiệm cận ngang.

Lời giải chi tiết

Dựa vào bảng biến thiên ta có:

• \(\mathop {\lim }\limits_{x \to - {2^ - }} f\left( x \right) = - \infty \).

Vậy \(x = - 2\) là tiệm cận đứng của đồ thị hàm số đã cho.

• \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty \).

Vậy hàm số không có tiệm cận ngang.

Chọn A.

Giải bài 55 trang 24 SBT Toán 12 Cánh Diều: Tổng quan và Phương pháp giải

Bài 55 trang 24 sách bài tập Toán 12 Cánh Diều thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.

Nội dung chi tiết bài 55 trang 24 SBT Toán 12 Cánh Diều

Để giải quyết bài 55 trang 24 SBT Toán 12 Cánh Diều một cách hiệu quả, bạn cần thực hiện các bước sau:

Xác định hàm số: Đọc kỹ đề bài để xác định chính xác hàm số cần xét.
Tính đạo hàm: Sử dụng các quy tắc tính đạo hàm để tìm đạo hàm cấp nhất của hàm số.
Tìm điểm cực trị: Giải phương trình đạo hàm bằng 0 để tìm các điểm cực trị của hàm số.
Xác định khoảng đơn điệu: Xét dấu đạo hàm trên các khoảng xác định để xác định khoảng đồng biến và nghịch biến của hàm số.
Kết luận: Dựa trên kết quả tìm được, đưa ra kết luận về tính chất của hàm số.

Đáp án chi tiết bài 55 trang 24 SBT Toán 12 Cánh Diều

Dưới đây là đáp án chi tiết cho bài 55 trang 24 SBT Toán 12 Cánh Diều. (Lưu ý: Đáp án cụ thể sẽ phụ thuộc vào nội dung từng câu hỏi trong bài tập.)

Ví dụ (giả định):

Cho hàm số y = x³ - 3x² + 2. Tìm các điểm cực trị của hàm số.

Giải:

Tính đạo hàm: y' = 3x² - 6x
Tìm điểm cực trị: 3x² - 6x = 0 => x = 0 hoặc x = 2
Xác định khoảng đơn điệu:
- Khi x < 0: y' > 0 => Hàm số đồng biến
- Khi 0 < x < 2: y' < 0 => Hàm số nghịch biến
- Khi x > 2: y' > 0 => Hàm số đồng biến
Kết luận: Hàm số có điểm cực đại tại x = 0, y = 2 và điểm cực tiểu tại x = 2, y = -2

Mẹo giải bài tập đạo hàm Toán 12

Để giải các bài tập về đạo hàm một cách nhanh chóng và chính xác, bạn có thể áp dụng một số mẹo sau:

Nắm vững các quy tắc tính đạo hàm: Việc hiểu rõ các quy tắc tính đạo hàm là nền tảng để giải quyết mọi bài toán.
Sử dụng bảng đạo hàm: Bảng đạo hàm sẽ giúp bạn tiết kiệm thời gian và tránh sai sót trong quá trình tính đạo hàm.
Phân tích kỹ đề bài: Đọc kỹ đề bài để xác định chính xác yêu cầu và các thông tin cần thiết.
Kiểm tra lại kết quả: Sau khi giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín

Tusach.vn là một website cung cấp đầy đủ các tài liệu học tập Toán 12, bao gồm sách giáo khoa, sách bài tập, đề thi và đáp án. Chúng tôi cam kết cung cấp cho bạn những tài liệu chất lượng, chính xác và cập nhật nhất. Hãy truy cập tusach.vn để học tốt môn Toán!

Hy vọng với bài giải chi tiết này, các bạn học sinh sẽ hiểu rõ hơn về cách giải bài 55 trang 24 SBT Toán 12 Cánh Diều và đạt kết quả tốt trong môn học.