Giải bài 81 trang 38 sách bài tập toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 81 trang 38 SBT Toán 12 Cánh Diều
Tusach.vn xin giới thiệu đáp án chi tiết bài 81 trang 38 Sách bài tập Toán 12 Cánh Diều. Bài giải được các thầy cô giáo có kinh nghiệm biên soạn, đảm bảo tính chính xác và dễ hiểu.
Chúng tôi luôn cố gắng cung cấp những tài liệu học tập tốt nhất để giúp các em học sinh ôn tập và nắm vững kiến thức Toán 12.
Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau: a) (y = frac{{2{rm{x}} - 1}}{{x + 1}}); b) (y = frac{x}{{x - 2}}); c) (y = frac{{{x^2} - 2{rm{x}} + 2}}{{ - x + 1}}); d) (y = frac{{{x^2} + 2{rm{x}} - 3}}{{x + 2}}).
Đề bài
Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:
a) \(y = \frac{{2{\rm{x}} - 1}}{{x + 1}}\);
b) \(y = \frac{x}{{x - 2}}\);
c) \(y = \frac{{{x^2} - 2{\rm{x}} + 2}}{{ - x + 1}}\);
d) \(y = \frac{{{x^2} + 2{\rm{x}} - 3}}{{x + 2}}\).
Phương pháp giải - Xem chi tiết
Sơ đồ khảo sát hàm số:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Xét sự biến thiên của hàm số
• Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm các đường tiệm cận của đồ thị (nếu có).
• Lập bảng biến thiên của hàm số, bao gồm: tính đạo hàm của hàm số, xét dấu đạo hàm, xét chiều biến thiên và tìm cực trị của hàm số (nếu có), điền các kết quả vào bảng.
Bước 3. Vẽ đồ thị hàm số
• Vẽ các đường tiệm cận (nếu có).
• Xác định các điểm đặc biệt của đồ thị: cực trị, giao điểm của đồ thị với các trục toạ độ (trong trường hợp đơn giản),…
• Nhận xét về đặc điểm của đồ thị: chỉ ra tâm đối xứng, trục đối xứng (nếu có).
Lời giải chi tiết
a) 1) Tập xác định: \(\mathbb{R}\backslash \left\{ { - 1} \right\}\).
2) Sự biến thiên:
• Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } y = 2;\mathop {\lim }\limits_{x \to - \infty } y = 2\).
Do đó, đường thẳng \(y = 2\) là tiệm cận ngang của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to - {1^ - }} y = + \infty ;\mathop {\lim }\limits_{x \to - {1^ + }} y = - \infty \).
Do đó, đường thẳng \(x = - 1\) là tiệm cận đứng của đồ thị hàm số.
• Bảng biến thiên:
\(y' = \frac{3}{{{{\left( {x + 1} \right)}^2}}} > 0,\forall x \in \mathbb{R}\backslash \left\{ { - 1} \right\}\).
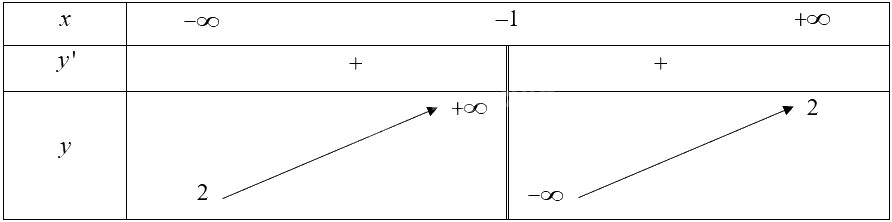
Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).
3) Đồ thị
• Giao điểm của đồ thị với trục tung: \(\left( {0; - 1} \right)\).
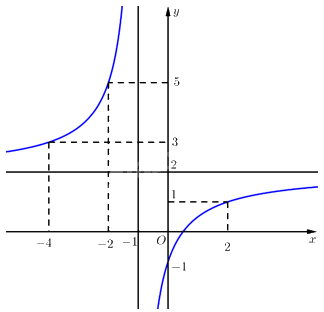
• Đồ thị hàm số đi qua các điểm: \(\left( { - 4;2} \right),\left( { - 2;5} \right),\left( {0; - 1} \right),\left( {2;1} \right)\).
Vậy đồ thị hàm số \(y = \frac{{2{\rm{x}} - 1}}{{x + 1}}\) như hình vẽ bên:
• Đồ thị hàm số nhận giao điểm \(I\left( { - 1;2} \right)\) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
b) 1) Tập xác định: \(\mathbb{R}\backslash \left\{ 2 \right\}\).
2) Sự biến thiên:
• Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } y = 1;\mathop {\lim }\limits_{x \to - \infty } y = 1\).
Do đó, đường thẳng \(y = 1\) là tiệm cận ngang của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty ;\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty \).
Do đó, đường thẳng \(x = 2\) là tiệm cận đứng của đồ thị hàm số.
• Bảng biến thiên:
\(y' = \frac{{ - 2}}{{{{\left( {x - 2} \right)}^2}}} < 0,\forall x \in \mathbb{R}\backslash \left\{ 2 \right\}\).
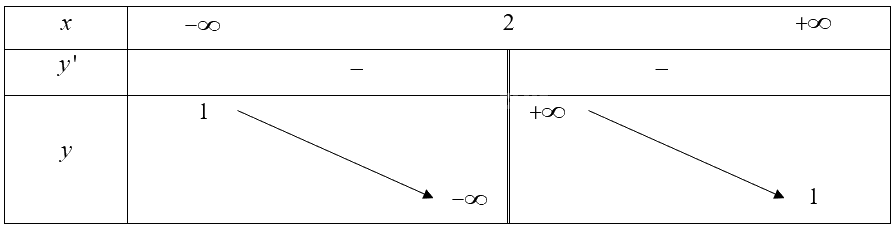
Hàm số nghịch biến trên các khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).
3) Đồ thị
• Giao điểm của đồ thị với trục tung: \(O\left( {0;0} \right)\).
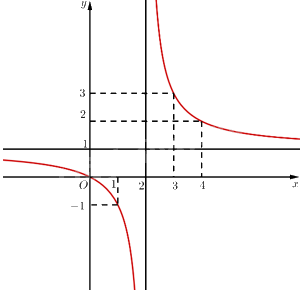
• Đồ thị hàm số đi qua các điểm: \(\left( {0;0} \right),\left( {1; - 1} \right),\left( {3;3} \right),\left( {4;2} \right)\).
Vậy đồ thị hàm số \(y = \frac{x}{{x - 2}}\) như hình vẽ bên:
• Đồ thị hàm số nhận giao điểm \(I\left( { - 1;2} \right)\) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
c) \(y = \frac{{{x^2} - 2{\rm{x}} + 2}}{{ - x + 1}} \Leftrightarrow y = - x + 1 + \frac{1}{{ - x + 1}}\)
1) Tập xác định: \(\mathbb{R}\backslash \left\{ 1 \right\}\).
2) Sự biến thiên:
• Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } y = - \infty ;\mathop {\lim }\limits_{x \to - \infty } y = + \infty \).
\(\mathop {\lim }\limits_{x \to {1^ - }} y = + \infty ;\mathop {\lim }\limits_{x \to {1^ + }} y = - \infty \).
Do đó, đường thẳng \(x = 1\) là tiệm cận đứng của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( { - x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{ - x + 1}} = 0;\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( { - x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{ - x + 1}} = 0\)
Do đó, đường thẳng \(y = - x + 1\) là tiệm cận xiên của đồ thị hàm số.
• Bảng biến thiên:
\(\begin{array}{l}y' = \frac{{{{\left( {{x^2} - 2{\rm{x}} + 2} \right)}^\prime }\left( { - x + 1} \right) - \left( {{x^2} - 2{\rm{x}} + 2} \right){{\left( { - x + 1} \right)}^\prime }}}{{{{\left( { - x + 1} \right)}^2}}}\\ & = \frac{{\left( {2{\rm{x}} - 2} \right)\left( { - x + 1} \right) - \left( {{x^2} - 2{\rm{x}} + 2} \right)\left( { - 1} \right)}}{{{{\left( { - x + 1} \right)}^2}}} = \frac{{ - {x^2} + 2{\rm{x}}}}{{{{\left( { - x + 1} \right)}^2}}}\end{array}\)
\(y' = 0 \Leftrightarrow - {x^2} + 2{\rm{x}} = 0 \Leftrightarrow x = 0\) hoặc \({\rm{x}} = 2\).
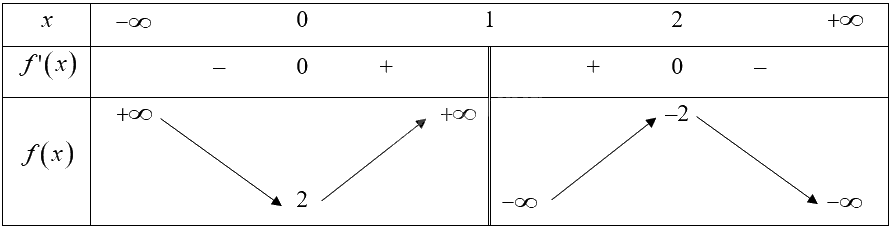
Hàm số nghịch biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\); đồng biến trên các khoảng \(\left( {0;1} \right)\) và \(\left( {1;2} \right)\).
Hàm số đạt cực tiểu tại \(x = 0,{y_{CT}} = 2\); đạt cực đại tại \(x = 2,{y_{CĐ}} = -2\).
3) Đồ thị
• Giao điểm của đồ thị với trục tung: \(\left( {0;2} \right)\).
• Đồ thị hàm số đi qua các điểm: \(\left( { - 1;\frac{5}{2}} \right),\left( {0;2} \right),\left( {2; - 2} \right),\left( {3; - \frac{5}{2}} \right)\).
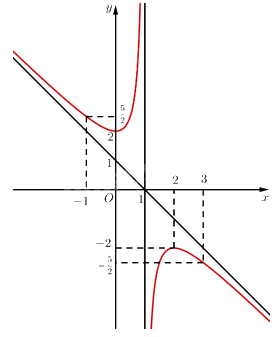
Vậy đồ thị hàm số \(y = \frac{{{x^2} - 2{\rm{x}} + 2}}{{ - x + 1}}\) như hình vẽ bên:
• Đồ thị hàm số nhận giao điểm \(I\left( {1;0} \right)\) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
d) \(y = \frac{{{x^2} + 2{\rm{x}} - 3}}{{x + 2}} \Leftrightarrow y = x - \frac{3}{{x + 2}}\)
1) Tập xác định: \(\mathbb{R}\backslash \left\{ { - 2} \right\}\).
2) Sự biến thiên:
• Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = - \infty \).
\(\mathop {\lim }\limits_{x \to - {2^ - }} y = + \infty ;\mathop {\lim }\limits_{x \to - {2^ + }} y = - \infty \).
Do đó, đường thẳng \(x = - 2\) là tiệm cận đứng của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 3}}{{x + 2}} = 0;\mathop {\lim }\limits_{x \to - \infty } \left[ {y - x} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - 3}}{{x + 2}} = 0\)
Do đó, đường thẳng \(y = x\) là tiệm cận xiên của đồ thị hàm số.
• Bảng biến thiên:
\(y' = 1 + \frac{3}{{{{\left( {x + 2} \right)}^2}}} > 0,\forall x \in \mathbb{R}\backslash \left\{ { - 2} \right\}\)
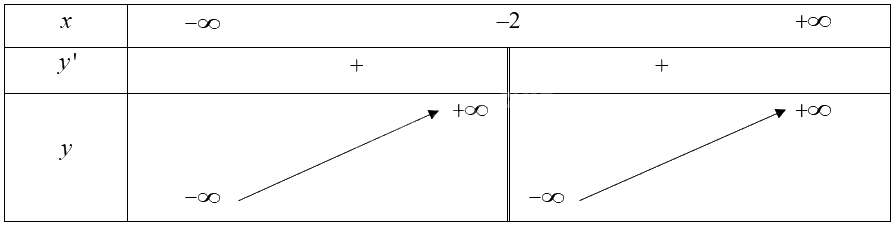
Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\).
3) Đồ thị
• Giao điểm của đồ thị với trục tung: \(\left( { - \frac{3}{2};0} \right)\).
• Đồ thị hàm số đi qua các điểm: \(\left( { - 5; - 4} \right),\left( { - 3;0} \right),\left( { - 1; - 4} \right),\left( {0; - \frac{3}{2}} \right),\left( {1;0} \right)\).
Vậy đồ thị hàm số \(y = \frac{{{x^2} + 2{\rm{x}} - 3}}{{x + 2}}\) như sau:
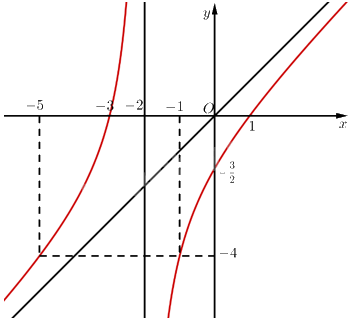
• Đồ thị hàm số nhận giao điểm \(I\left( {1;0} \right)\) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
Giải bài 81 trang 38 SBT Toán 12 Cánh Diều: Tổng quan
Bài 81 trang 38 Sách bài tập Toán 12 Cánh Diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về các chủ đề như đạo hàm, tích phân, hình học không gian và hình học giải tích. Bài tập này thường yêu cầu học sinh vận dụng các công thức, định lý đã học để giải quyết các bài toán thực tế.
Nội dung chi tiết bài 81 trang 38 SBT Toán 12 Cánh Diều
Để giúp các em học sinh hiểu rõ hơn về nội dung bài tập, Tusach.vn xin trình bày chi tiết lời giải của từng câu hỏi trong bài 81:
Câu a: (Nội dung câu a - ví dụ về một bài toán cụ thể)
Ví dụ: Tính đạo hàm của hàm số y = x3 - 2x2 + 5x - 1.
Lời giải:
y' = 3x2 - 4x + 5
Câu b: (Nội dung câu b - ví dụ về một bài toán cụ thể)
Ví dụ: Tính tích phân ∫01 x2 dx.
Lời giải:
∫01 x2 dx = [x3/3]01 = 1/3
Câu c: (Nội dung câu c - ví dụ về một bài toán cụ thể)
Ví dụ: Tìm phương trình mặt phẳng chứa điểm A(1; 2; 3) và vuông góc với vector pháp tuyến n = (1; -1; 2).
Lời giải:
Phương trình mặt phẳng có dạng: 1(x - 1) - 1(y - 2) + 2(z - 3) = 0 ⇔ x - y + 2z - 3 = 0
Mẹo giải bài tập Toán 12 Cánh Diều hiệu quả
- Nắm vững kiến thức cơ bản: Đảm bảo bạn hiểu rõ các định nghĩa, định lý, công thức đã học trong sách giáo khoa.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Sử dụng tài liệu tham khảo: Tham khảo các sách bài tập, đề thi thử để mở rộng kiến thức và tìm hiểu các phương pháp giải khác nhau.
- Tìm kiếm sự giúp đỡ: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo, bạn bè hoặc tìm kiếm sự trợ giúp trên các diễn đàn học tập trực tuyến.
Tại sao nên chọn Tusach.vn để giải bài tập Toán 12 Cánh Diều?
Tusach.vn là một website học tập uy tín, cung cấp đầy đủ và chính xác các đáp án, lời giải bài tập Toán 12 Cánh Diều. Chúng tôi cam kết:
- Đáp án chính xác 100%: Các đáp án được kiểm tra kỹ lưỡng bởi đội ngũ giáo viên có kinh nghiệm.
- Lời giải chi tiết, dễ hiểu: Lời giải được trình bày rõ ràng, logic, giúp các em học sinh dễ dàng nắm bắt kiến thức.
- Cập nhật liên tục: Chúng tôi luôn cập nhật các bài giải mới nhất để đáp ứng nhu cầu học tập của các em.
- Giao diện thân thiện, dễ sử dụng: Website được thiết kế trực quan, giúp các em dễ dàng tìm kiếm và truy cập thông tin.
Hãy truy cập Tusach.vn ngay hôm nay để giải bài tập Toán 12 Cánh Diều và đạt kết quả tốt nhất!
| Chủ đề | Liên kết |
|---|---|
| Giải bài tập Toán 12 Cánh Diều | https://tusach.vn/toan-12-canh-dieu |
| Đáp án Toán 12 Cánh Diều | https://tusach.vn/toan-12-canh-dieu/dap-an |