Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 4 trang 60 sách bài tập toán 12 - Cánh diều
SBT Toán 12 - Cánh diều
SBT TOÁN TẬP 1 - CÁNH DIỀU
Chương 2. Tọa độ của vecto trong không gian
Bài 1. Vecto và các phép toán vecto trong không gian

Giải bài 4 trang 60 sách bài tập toán 12 - Cánh diều

Giải bài 4 trang 60 SBT Toán 12 Cánh Diều

Tusach.vn xin giới thiệu lời giải chi tiết bài 4 trang 60 sách bài tập Toán 12 Cánh Diều. Bài giải này được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 12 Cánh Diều, đáp ứng nhu cầu học tập của học sinh.

Cho hình lập phương (ABCD.A'B'C'D'). Góc giữa hai vectơ (overrightarrow {BD} ,overrightarrow {B'C} ) bằng: A. ({30^ circ }). B. ({45^ circ }). C. ({120^ circ }). D. ({60^ circ }).

Đề bài

Cho hình lập phương \(ABCD.A'B'C'D'\). Góc giữa hai vectơ \(\overrightarrow {BD} ,\overrightarrow {B'C} \) bằng:

A. \({30^ \circ }\)

B. \({45^ \circ }\)

C. \({120^ \circ }\)

D. \({60^ \circ }\)

Phương pháp giải - Xem chi tiếtGiải bài 4 trang 60 sách bài tập toán 12 - Cánh diều 1

‒ Cách xác định góc giữa hai vectơ \(\overrightarrow a ,\overrightarrow b \): \(\left( {\overrightarrow a ,\overrightarrow b } \right) = \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right)\) với \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \).

Lời giải chi tiết

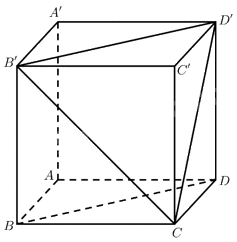
Giải bài 4 trang 60 sách bài tập toán 12 - Cánh diều 2

Ta có: \(\overrightarrow {B'D'} = \overrightarrow {B{\rm{D}}} \)

\( \Rightarrow \left( {\overrightarrow {BD} ,\overrightarrow {B'C} } \right) = \left( {\overrightarrow {B'D'} ,\overrightarrow {B'C} } \right) = \widehat {CB'D'}\).

Xét tam giác \(B'C{\rm{D}}'\) có \(B'C,C{\rm{D}}',B'D'\) đều là các đường chéo của các hình vuông là các mặt của hình lập phương.

Do đó \(B'C = C{\rm{D}}' = B'D'\). Vậy tam giác \(B'C{\rm{D}}'\) đều.

Suy ra \(\widehat {CB'D'} = {60^ \circ }\).

Vậy \(\left( {\overrightarrow {BD} ,\overrightarrow {B'C} } \right) = {60^ \circ }\).

Chọn D.

Giải bài 4 trang 60 SBT Toán 12 Cánh Diều: Tổng quan và Phương pháp giải

Bài 4 trang 60 sách bài tập Toán 12 Cánh Diều thuộc chương trình học Toán 12, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm như đạo hàm của hàm số, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.

Nội dung chi tiết bài 4 trang 60 SBT Toán 12 Cánh Diều

Để giải quyết bài 4 trang 60 SBT Toán 12 Cánh Diều một cách hiệu quả, học sinh cần thực hiện các bước sau:

  1. Xác định hàm số: Đọc kỹ đề bài để xác định chính xác hàm số cần xét.
  2. Tính đạo hàm: Sử dụng các quy tắc tính đạo hàm để tìm đạo hàm cấp nhất của hàm số.
  3. Tìm điểm cực trị: Giải phương trình đạo hàm bằng 0 để tìm các điểm nghi ngờ là điểm cực trị.
  4. Xác định loại điểm cực trị: Sử dụng dấu của đạo hàm cấp hai hoặc phương pháp xét dấu đạo hàm cấp nhất để xác định loại điểm cực trị (cực đại, cực tiểu).
  5. Kết luận: Viết kết luận về điểm cực trị và giá trị tương ứng.

Ví dụ minh họa giải bài 4 trang 60 SBT Toán 12 Cánh Diều

Đề bài: Tìm cực trị của hàm số y = x3 - 3x2 + 2.

Giải:

  • Tính đạo hàm: y' = 3x2 - 6x
  • Tìm điểm cực trị: 3x2 - 6x = 0 => x = 0 hoặc x = 2
  • Xác định loại điểm cực trị: y'' = 6x - 6
    • Tại x = 0: y'' = -6 < 0 => Hàm số đạt cực đại tại x = 0, ymax = 2
    • Tại x = 2: y'' = 6 > 0 => Hàm số đạt cực tiểu tại x = 2, ymin = -2
  • Kết luận: Hàm số đạt cực đại tại x = 0, ymax = 2 và đạt cực tiểu tại x = 2, ymin = -2.

Lưu ý khi giải bài 4 trang 60 SBT Toán 12 Cánh Diều

Để đạt kết quả tốt nhất khi giải bài 4 trang 60 SBT Toán 12 Cánh Diều, học sinh cần:

  • Nắm vững các kiến thức cơ bản về đạo hàm.
  • Luyện tập thường xuyên để rèn luyện kỹ năng giải toán.
  • Kiểm tra lại kết quả sau khi giải xong.
  • Tham khảo các nguồn tài liệu tham khảo khác để hiểu rõ hơn về bài toán.

Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín

Tusach.vn là một website cung cấp đầy đủ và chính xác các lời giải bài tập Toán 12 Cánh Diều, cùng với nhiều tài liệu học tập hữu ích khác. Chúng tôi cam kết mang đến cho học sinh những trải nghiệm học tập tốt nhất. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!

ChươngBàiLiên kết
1Bài 1Link bài 1
1Bài 2Link bài 2

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN