Giải bài 84 trang 39 SBT Toán 12 Cánh Diều

Giải bài 84 trang 39 sách bài tập toán 12 - Cánh diều

Tusach.vn xin giới thiệu đáp án chi tiết bài 84 trang 39 sách bài tập Toán 12 Cánh Diều. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Chúng tôi luôn cập nhật nhanh chóng và chính xác các bài giải SBT Toán 12 Cánh Diều, hỗ trợ tối đa cho quá trình học tập của bạn.

Kết luận nào sau đây là đúng đối với hàm số (y = {left( {frac{1}{2}} right)^{{x^2}}})? A. Hàm số đồng biến trên (mathbb{R}). B. Hàm số nghịch biến trên (mathbb{R}). C. Hàm số đồng biến trên khoảng (left( { - infty ;0} right)) và nghịch biến trên khoảng (left( {0; + infty } right)). D. Hàm số nghịch biến trên khoảng (left( { - infty ;0} right)) và đồng biến trên khoảng (left( {0; + infty } right)).

Đề bài

Kết luận nào sau đây là đúng đối với hàm số \(y = {\left( {\frac{1}{2}} \right)^{{x^2}}}\)?

A. Hàm số đồng biến trên \(\mathbb{R}\).

B. Hàm số nghịch biến trên \(\mathbb{R}\).

C. Hàm số đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).

D. Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\).

Phương pháp giải - Xem chi tiết Giải bài 84 trang 39 sách bài tập toán 12 - Cánh diều 1

Các bước để tìm khoảng đồng biến, nghịch biến của hàm số \(f\left( x \right)\):

Bước 1. Tìm tập xác định của hàm số \(y = f\left( x \right)\).

Bước 2. Tính đạo hàm \(f'\left( x \right)\). Tìm các điểm \({x_i}\left( {i = 1,2,...,n} \right)\) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.

Bước 3. Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập bảng biến thiên.

Bước 4. Căn cứ vào bảng biến thiên, nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

Lời giải chi tiết

Hàm số có tập xác định là \(\mathbb{R}\).

Ta có:

\(y' = ({x^2})'.{\left( {\frac{1}{2}} \right)^{{x^2}}}.\ln \frac{1}{2} = 2x.{\left( {\frac{1}{2}} \right)^{{x^2}}}.\ln \frac{1}{2} = 0 \Leftrightarrow x = 0\).

Bảng biến thiên của hàm số:

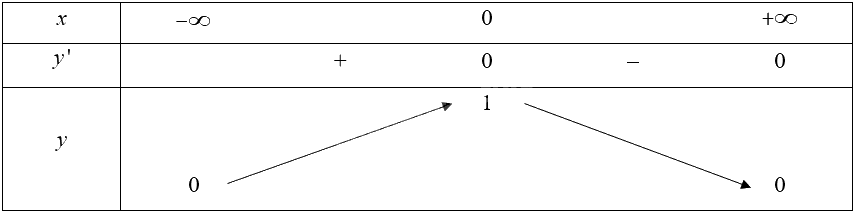
Giải bài 84 trang 39 sách bài tập toán 12 - Cánh diều 2

Vậy hàm số đồng biến trên khoảng \(\left( { - \infty ;0} \right)\); nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).

Chọn C.

Giải bài 84 trang 39 SBT Toán 12 Cánh Diều: Tổng quan và Phương pháp giải

Bài 84 trang 39 sách bài tập Toán 12 Cánh Diều thuộc chương trình học Toán 12, tập trung vào kiến thức về Số phức. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về phép toán trên số phức, tìm module của số phức, và giải các phương trình bậc hai với hệ số phức. Để giải quyết bài tập này một cách hiệu quả, bạn cần nắm vững các khái niệm và công thức cơ bản về số phức.

Nội dung chi tiết bài 84 trang 39 SBT Toán 12 Cánh Diều

Bài 84 thường bao gồm các dạng bài tập sau:

Dạng 1: Tính toán các phép toán trên số phức (cộng, trừ, nhân, chia).
Dạng 2: Tìm module của số phức.
Dạng 3: Giải phương trình bậc hai với hệ số phức.
Dạng 4: Ứng dụng số phức vào giải các bài toán hình học.

Đáp án chi tiết bài 84 trang 39 SBT Toán 12 Cánh Diều

Dưới đây là đáp án chi tiết cho từng phần của bài 84 trang 39 SBT Toán 12 Cánh Diều:

Ví dụ minh họa (Giả định nội dung bài tập):

Bài 84: Cho số phức z = 2 + 3i. Tính:

a) z + 1
b) z * (1 - i)
c) |z|

Giải:

a) z + 1 = (2 + 3i) + 1 = 3 + 3i
b) z * (1 - i) = (2 + 3i) * (1 - i) = 2 - 2i + 3i - 3i² = 2 + i + 3 = 5 + i
c) |z| = √(2² + 3²) = √13

Mẹo giải bài tập về số phức

Để giải các bài tập về số phức một cách nhanh chóng và chính xác, bạn nên:

Nắm vững các định nghĩa và tính chất của số phức.
Thành thạo các phép toán trên số phức.
Sử dụng công thức module của số phức một cách linh hoạt.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.

Tài liệu tham khảo hữu ích

Ngoài sách bài tập, bạn có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 12:

Sách giáo khoa Toán 12
Các trang web học Toán trực tuyến
Các video bài giảng Toán 12

Kết luận

Hy vọng với bài giải chi tiết và những lời khuyên trên, bạn đã có thể tự tin giải bài 84 trang 39 SBT Toán 12 Cánh Diều. Chúc bạn học tốt và đạt kết quả cao trong môn Toán!

Lưu ý: Bài giải trên chỉ mang tính chất tham khảo. Bạn nên tự mình giải bài tập để hiểu rõ hơn về kiến thức và rèn luyện kỹ năng giải toán.