Giải bài 8 trang 92 sách bài tập toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 8 trang 92 sách bài tập Toán 12 Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết bài 8 trang 92 sách bài tập Toán 12 Cánh Diều. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải dễ hiểu và các lưu ý quan trọng để giúp các em nắm vững kiến thức về chủ đề này.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.
Một thư viện thống kê số người đến đọc sách vào buổi tối trong 30 ngày của một tháng và kết quả được cho bởi Bảng 11. a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó. b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó (làm tròn kết quả đến hàng đơn vị).
Đề bài
Một thư viện thống kê số người đến đọc sách vào buổi tối trong 30 ngày của một tháng và kết quả được cho bởi Bảng 11.
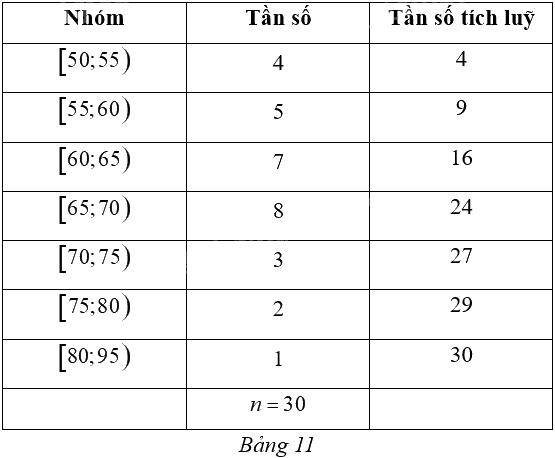
a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó.
b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó (làm tròn kết quả đến hàng đơn vị).
Phương pháp giải - Xem chi tiết
‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} - {a_1}\).
‒ Sử dụng công thức tính các tứ phân vị của mẫu số liệu ghép nhóm:
+ Nhóm thứ \(p\) là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{4}\) (tức là \(c{f_{p - 1}} < \frac{n}{4}\) nhưng \(c{f_p} \ge \frac{n}{4}\)). Ta gọi \(s,h,{n_p}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm \(p\), \(c{f_{p - 1}}\) là tần số tích luỹ của nhóm thứ \(p - 1\). Khi đó: \({Q_1} = s + \left( {\frac{{\frac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right).h\).
+ Nhóm thứ \(q\) là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{{3n}}{4}\) (tức là \(c{f_{q - 1}} < \frac{{3n}}{4}\) nhưng \(c{f_q} \ge \frac{{3n}}{4}\)). Ta gọi \(t,l,{n_q}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm \(q\), \(c{f_{q - 1}}\) là tần số tích luỹ của nhóm thứ \(q - 1\). Khi đó: \({Q_3} = t + \left( {\frac{{\frac{{3n}}{4} - c{f_{q - 1}}}}{{{n_q}}}} \right).l\).
‒ Sử dụng công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm: \(\Delta Q = {Q_3} - {Q_1}\).
Lời giải chi tiết
a) Khoảng biến thiên của mẫu số liệu ghép nhóm đó là: \(R = 90 - 40 = 40\) (người).
b) Nhóm 2 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{4} = \frac{{30}}{4} = 7,5\).
Nhóm 2 có đầu mút trái \(s = 55\), độ dài \(h = 5\), tần số của nhóm \({n_2} = 5\) và nhóm 1 có tần số tích luỹ \(c{f_1} = 4\).
Ta có: \({Q_1} = s + \left( {\frac{{7,5 - c{f_1}}}{{{n_2}}}} \right).h = 55 + \left( {\frac{{7,5 - 4}}{5}} \right).5 = 58,5\).
Nhóm 4 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{{3n}}{4} = \frac{{3.30}}{4} = 22,5\).
Nhóm 4 có đầu mút trái \(t = 65\), độ dài \(l = 5\), tần số của nhóm \({n_4} = 8\) và nhóm 3 có tần số tích luỹ \(c{f_3} = 16\).
Ta có: \({Q_3} = t + \left( {\frac{{22,5 - c{f_3}}}{{{n_4}}}} \right).l = 65 + \left( {\frac{{22,5 - 16}}{8}} \right).5 = 69,0625\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \(\Delta Q = {Q_3} - {Q_1} = 69,0625 - 58,5 \approx 11\) (người).
Giải bài 8 trang 92 SBT Toán 12 Cánh Diều: Tổng quan và Phương pháp giải
Bài 8 trang 92 sách bài tập Toán 12 Cánh Diều thuộc chương trình học môn Toán lớp 12, tập trung vào việc ôn tập và củng cố kiến thức về các chủ đề đã học. Bài tập thường bao gồm các dạng bài tập về đạo hàm, tích phân, hình học không gian và các ứng dụng của đạo hàm trong thực tế.
Nội dung chi tiết bài 8 trang 92 SBT Toán 12 Cánh Diều
Để giải quyết bài 8 trang 92 một cách hiệu quả, các em cần nắm vững các kiến thức sau:
- Đạo hàm: Hiểu rõ các quy tắc tính đạo hàm của các hàm số cơ bản, đạo hàm của hàm hợp, đạo hàm của hàm ẩn.
- Tích phân: Nắm vững các phương pháp tính tích phân, tích phân từng phần, tích phân bằng phương pháp đổi biến.
- Hình học không gian: Hiểu rõ các khái niệm về đường thẳng, mặt phẳng, khoảng cách trong không gian.
- Ứng dụng của đạo hàm: Biết cách sử dụng đạo hàm để giải các bài toán về cực trị, điểm uốn, khảo sát hàm số.
Giải chi tiết từng bài tập trong bài 8 trang 92 SBT Toán 12 Cánh Diều
Dưới đây là giải chi tiết từng bài tập trong bài 8 trang 92 sách bài tập Toán 12 Cánh Diều:
Bài 8.1 trang 92 SBT Toán 12 Cánh Diều
Đề bài: (Ví dụ về đề bài)
Giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện và giải thích rõ ràng)
Bài 8.2 trang 92 SBT Toán 12 Cánh Diều
Đề bài: (Ví dụ về đề bài)
Giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện và giải thích rõ ràng)
(Tiếp tục giải chi tiết các bài tập còn lại trong bài 8)
Lưu ý khi giải bài 8 trang 92 SBT Toán 12 Cánh Diều
Để đạt kết quả tốt nhất khi giải bài 8 trang 92, các em cần lưu ý những điều sau:
- Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
- Sử dụng các công thức và định lý một cách chính xác.
- Kiểm tra lại kết quả sau khi giải xong.
- Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng.
Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn là một website cung cấp tài liệu học tập Toán 12 uy tín và chất lượng. Chúng tôi cung cấp đầy đủ các giải bài tập, đáp án, lý thuyết và các bài giảng video giúp các em học tập hiệu quả. Ngoài ra, chúng tôi còn có đội ngũ giáo viên giàu kinh nghiệm sẵn sàng giải đáp mọi thắc mắc của các em.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác!
Bảng tổng hợp các dạng bài tập thường gặp
| Dạng bài tập | Kiến thức liên quan | Ví dụ |
|---|---|---|
| Tính đạo hàm | Quy tắc tính đạo hàm | Tính đạo hàm của hàm số y = x^2 + 3x - 1 |
| Giải phương trình | Phương pháp giải phương trình | Giải phương trình x^2 - 5x + 6 = 0 |