Giải bài 50 trang 27 sách bài tập toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 50 trang 27 SBT Toán 12 Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 50 trang 27 sách bài tập Toán 12 Cánh Diều. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác đáp án các bài tập trong SBT Toán 12 Cánh Diều.
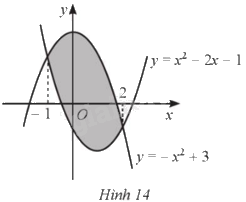
Cho hình phẳng được tô màu như Hình 14. a) Hình phẳng đó được giới hạn bởi các đường nào? b) Tính diện tích hình phẳng đó.
Đề bài
Cho hình phẳng được tô màu như Hình 14.
a) Hình phẳng đó được giới hạn bởi các đường nào?
b) Tính diện tích hình phẳng đó.
Phương pháp giải - Xem chi tiết
Sử dụng công thức: Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số \(y = f\left( x \right),y = g\left( x \right)\) và hai đường thẳng \(x = a,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Lời giải chi tiết
a) Hình phẳng đã cho được giới hạn bởi đồ thị các hàm số \(y = {x^2} - 2{\rm{x}} - 1,y = - {x^2} + 3\) và hai đường thẳng \(x = - 1,x = 2\).
b) Diện tích hình phẳng được tính theo công thức:
\(\begin{array}{l}S = \int\limits_{ - 1}^2 {\left| {\left( {{x^2} - 2{\rm{x}} - 1} \right) - \left( { - {x^2} + 3} \right)} \right|dx} = \int\limits_{ - 1}^2 {\left[ {\left( { - {x^2} + 3} \right) - \left( {{x^2} - 2{\rm{x}} - 1} \right)} \right]dx} = \int\limits_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)dx} \\ = \left. {\left[ { - \frac{{2{{\rm{x}}^3}}}{3} + {x^2} + 4{\rm{x}}} \right]} \right|_{ - 1}^2 = \frac{{20}}{3} - \left( { - \frac{7}{3}} \right) = 9\end{array}\)
Giải bài 50 trang 27 SBT Toán 12 Cánh Diều: Tổng quan và Phương pháp giải
Bài 50 trang 27 sách bài tập Toán 12 Cánh Diều thuộc chương trình học Toán 12, tập trung vào chủ đề về Đường thẳng và Mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về vectơ, phương trình đường thẳng, phương trình mặt phẳng để giải quyết các bài toán liên quan đến quan hệ vị trí giữa đường thẳng và mặt phẳng.
Nội dung chi tiết bài 50 trang 27 SBT Toán 12 Cánh Diều
Bài 50 thường bao gồm các dạng bài tập sau:
- Xác định vị trí tương đối giữa đường thẳng và mặt phẳng: Kiểm tra xem đường thẳng có nằm trong mặt phẳng, song song với mặt phẳng, cắt mặt phẳng hay không.
- Tìm giao điểm của đường thẳng và mặt phẳng: Nếu đường thẳng cắt mặt phẳng, cần tìm tọa độ giao điểm.
- Tính góc giữa đường thẳng và mặt phẳng: Sử dụng công thức tính góc giữa đường thẳng và mặt phẳng dựa trên vectơ chỉ phương của đường thẳng và vectơ pháp tuyến của mặt phẳng.
- Tìm hình chiếu của đường thẳng lên mặt phẳng: Xác định đường thẳng là hình chiếu của đường thẳng ban đầu lên mặt phẳng.
Phương pháp giải bài 50 trang 27 SBT Toán 12 Cánh Diều
Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
- Vectơ: Hiểu rõ các phép toán vectơ, tích vô hướng, tích có hướng.
- Phương trình đường thẳng: Biết cách viết phương trình đường thẳng dưới các dạng khác nhau (dạng tham số, dạng chính tắc).
- Phương trình mặt phẳng: Biết cách viết phương trình mặt phẳng.
- Quan hệ vị trí giữa đường thẳng và mặt phẳng: Nắm vững các điều kiện để xác định vị trí tương đối giữa đường thẳng và mặt phẳng.
Lời giải chi tiết bài 50 trang 27 SBT Toán 12 Cánh Diều (Ví dụ)
Bài toán: Cho đường thẳng d: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P): 2x - y + z - 5 = 0. Xác định vị trí tương đối giữa d và (P).
Lời giải:
Vectơ chỉ phương của d là a = (1, -1, 2). Vectơ pháp tuyến của (P) là n = (2, -1, 1).
Ta có a.n = 1*2 + (-1)*(-1) + 2*1 = 2 + 1 + 2 = 5 ≠ 0. Do đó, đường thẳng d và mặt phẳng (P) cắt nhau.
Lưu ý khi giải bài tập
- Luôn kiểm tra lại các phép tính vectơ.
- Vẽ hình minh họa để dễ dàng hình dung bài toán.
- Sử dụng các công thức một cách chính xác.
Tusach.vn - Hỗ trợ học tập Toán 12 hiệu quả
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách bài tập Toán 12 Cánh Diều. Chúng tôi cam kết mang đến cho bạn trải nghiệm học tập tốt nhất. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Chủ đề | Liên kết |
|---|---|
| Giải SBT Toán 12 Cánh Diều | Tusach.vn |
| Đường thẳng và Mặt phẳng | Link đến bài giảng |