Giải bài 17 trang 13 sách bài tập toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 17 trang 13 SBT Toán 12 Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 17 trang 13 sách bài tập Toán 12 Cánh Diều. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp những nội dung chất lượng nhất để hỗ trợ các em học tập hiệu quả.
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Cho hàm số (y = {x^3} - 3{rm{x}} + 2). a) (y' = 3{{rm{x}}^2} - 3). b) (y' = 0) khi (x = - 1,x = 1). c) (y' > 0) khi (x in left( { - 1;1} right)) và (y' < 0) khi (x in left( { - infty ; - 1} right) cup left( {1; + infty } right)). d) Giá trị cực đại của hàm số là ${{f}_{CĐ}}=0$.
Đề bài
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).
Cho hàm số \(y = {x^3} - 3{\rm{x}} + 2\).a) \(y' = 3{{\rm{x}}^2} - 3\).b) \(y' = 0\) khi \(x = - 1,x = 1\).c) \(y' > 0\) khi \(x \in \left( { - 1;1} \right)\) và \(y' < 0\) khi \(x \in \left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\).d) Giá trị cực đại của hàm số là ${{f}_{C}}=0$.
Phương pháp giải - Xem chi tiết
Lập bảng biến thiên của hàm số \(y = f\left( x \right)\), từ đó xác định các khoảng đơn điệu, cực trị của hàm số \(y = f\left( x \right)\).
Lời giải chi tiết
Hàm số có tập xác định là \(\mathbb{R}\).
Ta có:
\(y' = 3{{\rm{x}}^2} - 3\). Vậy a) đúng.
\(y' = 0\) khi \(x = - 1,x = 1\). Vậy b) đúng.
Bảng biến thiên của hàm số:
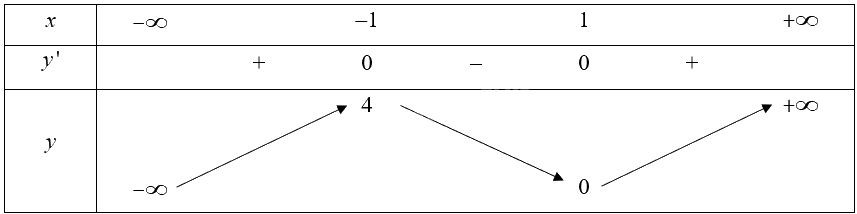
Vậy hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\); nghịch biến trên khoảng \(\left( { - 1;1} \right)\). Vậy c) sai.
Hàm số đạt cực đại tại \(x = - 1\). Khi đó giá trị cực đại ${{f}_{CĐ}}=4$. Vậy d) sai.
a) Đ. b) Đ. c) S. d) S.
Giải bài 17 trang 13 SBT Toán 12 Cánh Diều: Tổng quan
Bài 17 trang 13 SBT Toán 12 Cánh Diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về đạo hàm. Bài tập này yêu cầu học sinh vận dụng các công thức và quy tắc đạo hàm đã học để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức về đạo hàm là vô cùng quan trọng, không chỉ cho kỳ thi THPT Quốc gia mà còn là nền tảng cho các môn học ở bậc đại học.
Nội dung chi tiết bài 17 trang 13 SBT Toán 12 Cánh Diều
Bài 17 bao gồm một số câu hỏi trắc nghiệm và bài tập tự luận. Các câu hỏi trắc nghiệm thường kiểm tra khả năng hiểu và vận dụng các công thức đạo hàm cơ bản. Các bài tập tự luận yêu cầu học sinh phải trình bày lời giải chi tiết, rõ ràng, thể hiện quá trình suy luận logic và khả năng giải quyết vấn đề.
Hướng dẫn giải chi tiết từng câu hỏi
- Câu 1: (Trích dẫn câu hỏi) - Giải thích cách tiếp cận và áp dụng công thức đạo hàm phù hợp. Ví dụ: Để tính đạo hàm của hàm số f(x) = x2 + 2x - 1, ta sử dụng quy tắc đạo hàm của tổng và đạo hàm của lũy thừa: f'(x) = 2x + 2.
- Câu 2: (Trích dẫn câu hỏi) - Phân tích các bước giải và đưa ra kết quả cuối cùng. Ví dụ: Nếu câu hỏi yêu cầu tìm đạo hàm bậc hai, ta cần đạo hàm hàm số một lần, sau đó đạo hàm kết quả vừa tìm được.
- Câu 3: (Trích dẫn câu hỏi) - Lưu ý các điểm quan trọng và các lỗi thường gặp. Ví dụ: Khi đạo hàm hàm hợp, cần sử dụng quy tắc chuỗi.
- ... (Các câu hỏi tiếp theo) - Tiếp tục giải thích và hướng dẫn giải chi tiết cho từng câu hỏi.
Các dạng bài tập thường gặp trong bài 17
- Dạng 1: Tính đạo hàm của hàm số đơn thức.
- Dạng 2: Tính đạo hàm của hàm số đa thức.
- Dạng 3: Tính đạo hàm của hàm số lượng giác.
- Dạng 4: Tính đạo hàm của hàm số mũ và logarit.
- Dạng 5: Tính đạo hàm của hàm hợp.
Mẹo giải nhanh và hiệu quả
Để giải nhanh và hiệu quả các bài tập về đạo hàm, bạn nên:
- Nắm vững các công thức đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để kiểm tra kết quả.
- Đọc kỹ đề bài và xác định đúng các yếu tố cần tìm.
Tài liệu tham khảo hữu ích
Ngoài sách bài tập, bạn có thể tham khảo thêm các tài liệu sau:
- Sách giáo khoa Toán 12
- Các trang web học Toán trực tuyến
- Các video hướng dẫn giải bài tập Toán 12
Kết luận
Hy vọng với lời giải chi tiết và hướng dẫn giải bài 17 trang 13 SBT Toán 12 Cánh Diều trên đây, các em học sinh sẽ hiểu rõ hơn về kiến thức đạo hàm và tự tin giải quyết các bài tập tương tự. Chúc các em học tập tốt!