Giải bài 79 trang 38 sách bài tập toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 79 trang 38 SBT Toán 12 Cánh Diều
Tusach.vn xin giới thiệu đáp án chi tiết bài 79 trang 38 sách bài tập Toán 12 Cánh Diều. Bài giải được các thầy cô giáo có kinh nghiệm biên soạn, đảm bảo tính chính xác và dễ hiểu.
Chúng tôi luôn cố gắng cung cấp những tài liệu học tập tốt nhất để giúp các em học sinh nắm vững kiến thức và đạt kết quả cao trong các kỳ thi.
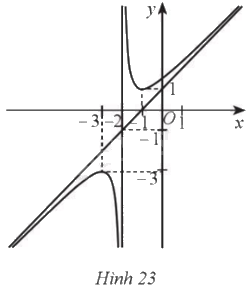
Cho hàm số (y = fleft( x right) = frac{{a{x^2} + bx + c}}{{mx + n}}) (với (a,m ne 0)) có đồ thị là đường cong như Hình 23. Căn cứ vào đồ thị hàm số: a) Tìm khoảng đơn điệu, điểm cực đại, cực tiểu của hàm số. b) Viết phương trình đường tiệm cận đứng, tiệm cận xiên của đồ thị hàm số. c) Phương trình (fleft( x right) = 3) có bao nhiêu nghiệm? d) Tìm công thức xác định hàm số (y = fleft( x right)), biết (m = 1).
Đề bài
Cho hàm số \(y = f\left( x \right) = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (với \(a,m \ne 0\)) có đồ thị là đường cong như Hình 23. Căn cứ vào đồ thị hàm số:
a) Tìm khoảng đơn điệu, điểm cực đại, cực tiểu của hàm số.
b) Viết phương trình đường tiệm cận đứng, tiệm cận xiên của đồ thị hàm số.
c) Phương trình \(f\left( x \right) = 3\) có bao nhiêu nghiệm?
d) Tìm công thức xác định hàm số \(y = f\left( x \right)\), biết \(m = 1\).
Phương pháp giải - Xem chi tiết
‒ Xét đồ thị hàm số.
‒ Xét các đường tiệm cận của đồ thị hàm số.
‒ Xét các điểm trên đồ thị hàm số.
Lời giải chi tiết
a) Dựa vào đồ thị hàm số, ta có:
‒ Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 3} \right)\) và \(\left( { - 1; + \infty } \right)\); nghịch biến trên các khoảng \(\left( { - 3; - 2} \right)\) và \(\left( { - 2; - 1} \right)\).
‒ Hàm số đạt cực đại tại điểm \(x = - 3\), đạt cực tiểu tại điểm \(x = - 1\).
b)
• Tiệm cận đứng của đồ thị hàm số đi qua điểm có hoành độ ‒2.
Vậy \(x = - 2\) là tiệm cận đứng của đồ thị hàm số.
• Tiệm cận xiên của đồ thị hàm số đi qua hai điểm \(\left( { - 1;0} \right)\) và \(\left( { - 2; - 1} \right)\).
Vậy đường thẳng \(y = x + 1\) là tiệm cận xiên của đồ thị hàm số.
c) Đường thẳng \(y = 3\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 2 điểm. Vậy phương trình \(f\left( x \right) = 3\) có 2 nghiệm.
d) Đồ thị hàm số có \(x = - 2\) là tiệm cận đứng. Vậy \( - \frac{n}{m} = - 2 \Leftrightarrow - \frac{n}{1} = - 2 \Leftrightarrow n = 2\).
Tiệm cận xiên của đồ thị hàm số có hệ số góc bằng 1. Vậy \(\frac{a}{m} = 1 \Leftrightarrow \frac{a}{1} = 1 \Leftrightarrow a = 1\).
Đồ thị hàm số đi qua điểm \(\left( { - 1;1} \right)\) nên ta có: \(\frac{{1.{{\left( { - 1} \right)}^2} + b.\left( { - 1} \right) + c}}{{\left( { - 1} \right) + 2}} = 1 \Leftrightarrow - b + c = 0\).
Đồ thị hàm số đi qua điểm \(\left( { - 3; - 3} \right)\) nên ta có: \(\frac{{1.{{\left( { - 3} \right)}^2} + b.\left( { - 3} \right) + c}}{{\left( { - 3} \right) + 2}} = - 3 \Leftrightarrow - 3b + c = - 6\).
Từ đó ta có \(b = 3,c = 3\).
Vậy hàm số cần tìm là: \(y = f\left( x \right) = \frac{{{x^2} + 3{\rm{x}} + 3}}{{{\rm{x}} + 2}}\).
Giải bài 79 trang 38 SBT Toán 12 Cánh Diều: Tổng quan
Bài 79 trang 38 sách bài tập Toán 12 Cánh Diều thuộc chương trình học Toán 12, tập trung vào chủ đề về Đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về vectơ chỉ phương, vectơ pháp tuyến, phương trình đường thẳng, phương trình mặt phẳng để giải quyết các bài toán liên quan đến vị trí tương đối giữa đường thẳng và mặt phẳng, khoảng cách từ điểm đến mặt phẳng, và các bài toán ứng dụng thực tế.
Nội dung chi tiết bài 79 trang 38 SBT Toán 12 Cánh Diều
Bài 79 thường bao gồm các dạng bài tập sau:
- Dạng 1: Xác định phương trình đường thẳng và mặt phẳng. Học sinh cần xác định các yếu tố cần thiết như điểm thuộc đường thẳng/mặt phẳng, vectơ chỉ phương/vectơ pháp tuyến để viết phương trình.
- Dạng 2: Tìm giao điểm của đường thẳng và mặt phẳng. Sử dụng phương pháp thế hoặc phương pháp tọa độ để tìm tọa độ giao điểm.
- Dạng 3: Tính khoảng cách từ điểm đến mặt phẳng. Áp dụng công thức tính khoảng cách từ điểm đến mặt phẳng.
- Dạng 4: Xác định vị trí tương đối giữa đường thẳng và mặt phẳng. Kiểm tra xem đường thẳng song song, vuông góc hay cắt mặt phẳng.
Hướng dẫn giải bài 79 trang 38 SBT Toán 12 Cánh Diều (Ví dụ minh họa)
Ví dụ: Cho đường thẳng d: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P): 2x - y + z - 5 = 0. Tìm tọa độ giao điểm của d và (P).
Giải:
- Thay phương trình tham số của đường thẳng d vào phương trình mặt phẳng (P): 2(1+t) - (2-t) + (3+2t) - 5 = 0
- Giải phương trình để tìm t: 2 + 2t - 2 + t + 3 + 2t - 5 = 0 => 5t - 2 = 0 => t = 2/5
- Thay t = 2/5 vào phương trình tham số của đường thẳng d để tìm tọa độ giao điểm: x = 1 + 2/5 = 7/5, y = 2 - 2/5 = 8/5, z = 3 + 2(2/5) = 19/5
- Vậy giao điểm của d và (P) là I(7/5, 8/5, 19/5).
Lưu ý khi giải bài tập về đường thẳng và mặt phẳng
- Nắm vững các công thức và định lý liên quan đến vectơ, phương trình đường thẳng, phương trình mặt phẳng.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng hình vẽ để minh họa và hiểu rõ hơn về bài toán.
- Kiểm tra lại kết quả sau khi giải để đảm bảo tính chính xác.
Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn là địa chỉ tin cậy cung cấp đáp án, lời giải chi tiết và các tài liệu học tập Toán 12 chất lượng. Chúng tôi luôn cập nhật những thông tin mới nhất và hữu ích nhất để giúp các em học sinh học tập hiệu quả. Ngoài giải bài 79 trang 38 SBT Toán 12 Cánh Diều, các em có thể tìm thấy lời giải cho các bài tập khác trong sách bài tập và sách giáo khoa Toán 12 Cánh Diều tại tusach.vn.
Chúc các em học tập tốt!