Giải bài 82 trang 38 sách bài tập toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 82 trang 38 SBT Toán 12 Cánh Diều
Tusach.vn xin giới thiệu đáp án chi tiết bài 82 trang 38 Sách bài tập Toán 12 Cánh Diều. Bài giải được các thầy cô giáo có kinh nghiệm biên soạn, đảm bảo tính chính xác và dễ hiểu.
Chúng tôi luôn cố gắng cung cấp những tài liệu học tập tốt nhất để giúp các em học sinh nắm vững kiến thức và đạt kết quả cao trong các kỳ thi.
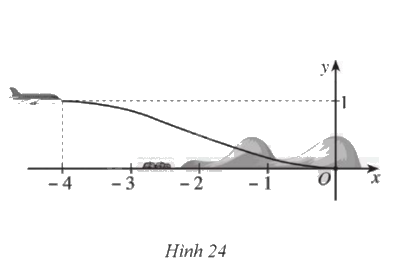
Một máy bay loại nhỏ bắt đầu hạ cánh, đường bay của nó khi gắn với hệ trục toạ độ (Oxy) được mô phỏng ở Hình 24. Biết đường bay của nó có dạng đồ thị hàm số bậc ba; vị trí bắt đầu hạ cánh có toạ độ (left( { - 4;1} right)) là điểm cực đại của đồ thị hàm số và máy bay tiếp đất tại vị trí gốc toạ độ là điểm cực tiểu của đồ thị hàm số. a) Tìm công thức xác định hàm số mô phỏng đường bay của máy bay trên đoạn (left[ { - 4;0} right]). b) Khi máy bay cách vị trí hạ cánh theo phương ngang 3
Đề bài
Một máy bay loại nhỏ bắt đầu hạ cánh, đường bay của nó khi gắn với hệ trục toạ độ \(Oxy\) được mô phỏng ở Hình 24. Biết đường bay của nó có dạng đồ thị hàm số bậc ba; vị trí bắt đầu hạ cánh có toạ độ \(\left( { - 4;1} \right)\) là điểm cực đại của đồ thị hàm số và máy bay tiếp đất tại vị trí gốc toạ độ là điểm cực tiểu của đồ thị hàm số.
a) Tìm công thức xác định hàm số mô phỏng đường bay của máy bay trên đoạn \(\left[ { - 4;0} \right]\).
b) Khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay cách mặt đất bao nhiêu dặm? (Biết đơn vị trên hệ trục toạ độ là dặm).
c) Khi ở độ cao 0,5 dặm, máy bay cách vị trí hạ cánh theo phương ngang bao nhiều dặm?
Phương pháp giải - Xem chi tiết
‒ Tìm công thức xác định hàm số mô phỏng đường bay của máy bay trên đoạn \(\left[ { - 4;0} \right]\) dựa vào các điểm trên đồ thị hàm số và các điểm cực trị.
‒ Dựa vào công thức của hàm số để tính khoảng cách giữa máy bay với mặt đất và vị trí hạ cánh theo phương ngang.
Lời giải chi tiết
a) Giả sử đường bay của máy bay có dạng là đồ thị của hàm số \(y = a{x^3} + b{{\rm{x}}^2} + c{\rm{x}} + d\) \(\left( {a \ne 0} \right)\) trên đoạn \(\left[ { - 4;0} \right]\).
\(y' = 3a{x^2} + 2b{\rm{x}} + c\)
Đồ thị hàm số đi qua điểm \(\left( {0;0} \right)\) nên ta có: \(a{.0^3} + b{.0^2} + c.0 + d = 0 \Leftrightarrow d = 0\)
\(x = 0\) là điểm cực tiểu của đồ thị hàm số nên ta có:
\(3a{.0^2} + 2b.0 + c = 0 \Leftrightarrow c = 0\).
Đồ thị hàm số đi qua điểm \(\left( { - 4;1} \right)\) nên ta có:
\(a.{\left( { - 4} \right)^3} + b.{\left( { - 4} \right)^2} + 0.\left( { - 4} \right) + 0 = 1 \Leftrightarrow - 64a + 16b = 1\).
\(x = - 4\) là điểm cực đại của đồ thị hàm số nên ta có:
\(3a.{\left( { - 4} \right)^2} + 2b.\left( { - 4} \right) = 0 \Leftrightarrow 48a - 8b = 0\).
Từ đó ta có \(a = \frac{1}{{32}},b = \frac{3}{{16}},c = 0\).
Vậy hàm số cần tìm là: \(y = \frac{1}{{32}}{x^3} + \frac{3}{{16}}{{\rm{x}}^2}\).
b) Thay \(x = - 3\), ta được: \(y = \frac{1}{{32}}.{\left( { - 3} \right)^3} + \frac{3}{{16}}.{\left( { - 3} \right)^2} = \frac{{27}}{{32}}\).
Vậy khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay cách mặt đất \(\frac{{27}}{{32}} = 0,84375\) (dặm).
c) Thay \(y = 0,5\) ta được \(\frac{1}{{32}}{x^3} + \frac{3}{{16}}{{\rm{x}}^2} = 0,5 \Leftrightarrow x = - 2 - 2\sqrt 3 ,x = - 2 + 2\sqrt 3 ,x = - 2\).
Do \(x \in \left[ { - 4;0} \right]\) nên \(x = - 2\).
Vậy khi ở độ cao 0,5 dặm, máy bay cách vị trí hạ cánh theo phương ngang 2 dặm.
Giải bài 82 trang 38 SBT Toán 12 Cánh Diều: Tổng quan và Phương pháp giải
Bài 82 trang 38 Sách bài tập Toán 12 Cánh Diều thuộc chương trình học Toán 12, tập trung vào kiến thức về Đạo hàm của hàm số hợp. Bài tập này yêu cầu học sinh vận dụng các quy tắc đạo hàm, đặc biệt là quy tắc đạo hàm hàm hợp, để tính đạo hàm của các hàm số phức tạp. Việc nắm vững quy tắc này là vô cùng quan trọng, không chỉ cho việc giải bài tập này mà còn cho các bài tập và ứng dụng khác trong chương trình học.
Nội dung chi tiết bài 82 trang 38 SBT Toán 12 Cánh Diều
Bài 82 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh tính đạo hàm của các hàm số sau:
- Câu a: y = sin(x2 + 1)
- Câu b: y = cos(2x - 3)
- Câu c: y = tan(x3)
- Câu d: y = esin(x)
Phương pháp giải bài 82 trang 38 SBT Toán 12 Cánh Diều
Để giải bài 82, học sinh cần áp dụng quy tắc đạo hàm hàm hợp, được phát biểu như sau:
Nếu y = f(u) và u = g(x) thì dy/dx = (dy/du) * (du/dx)
Áp dụng quy tắc này, ta có thể giải từng câu như sau:
Giải câu a: y = sin(x2 + 1)
- Đặt u = x2 + 1
- Khi đó y = sin(u)
- dy/du = cos(u)
- du/dx = 2x
- dy/dx = (dy/du) * (du/dx) = cos(u) * 2x = cos(x2 + 1) * 2x = 2xcos(x2 + 1)
Giải câu b: y = cos(2x - 3)
Tương tự như câu a, ta đặt u = 2x - 3, y = cos(u). Áp dụng quy tắc đạo hàm hàm hợp, ta được:
dy/dx = -sin(2x - 3) * 2 = -2sin(2x - 3)
Giải câu c: y = tan(x3)
Đặt u = x3, y = tan(u). Áp dụng quy tắc đạo hàm hàm hợp, ta được:
dy/dx = (1/cos2(u)) * 3x2 = (3x2)/cos2(x3)
Giải câu d: y = esin(x)
Đặt u = sin(x), y = eu. Áp dụng quy tắc đạo hàm hàm hợp, ta được:
dy/dx = eu * cos(x) = esin(x) * cos(x)
Lưu ý khi giải bài tập về đạo hàm hàm hợp
- Xác định đúng hàm trong và hàm ngoài.
- Nắm vững các công thức đạo hàm cơ bản.
- Thực hành nhiều bài tập để làm quen với các dạng bài khác nhau.
Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn là địa chỉ tin cậy cung cấp đáp án, lời giải chi tiết và các tài liệu học tập Toán 12 chất lượng. Chúng tôi luôn cập nhật những thông tin mới nhất và hữu ích nhất để giúp các em học sinh học tập hiệu quả. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Câu | Đáp án |
|---|---|
| a | 2xcos(x2 + 1) |
| b | -2sin(2x - 3) |
| c | (3x2)/cos2(x3) |
| d | esin(x) * cos(x) |