Giải bài 10 trang 12 sách bài tập toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 10 trang 12 SBT Toán 12 Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 10 trang 12 sách bài tập Toán 12 Cánh Diều. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác đáp án các bài tập trong sách bài tập Toán 12 Cánh Diều.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau: Mệnh đề nào dưới đây đúng? A. Hàm số đạt cực tiểu tại \(x = - 5\). B. Hàm số có giá trị cực đại bằng 0. C. Hàm số đạt cực tiểu tại \(x = 2\). D. Hàm số đạt cực đại tại \(x = 4\).
Đề bài
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
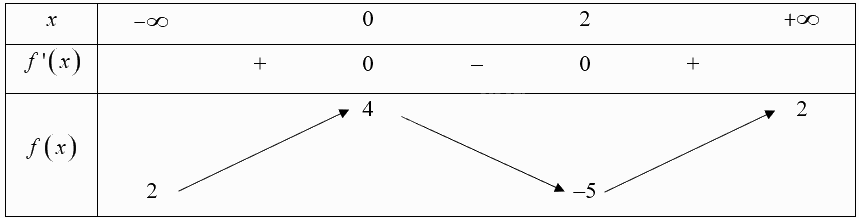
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực tiểu tại \(x = - 5\). B. Hàm số có giá trị cực đại bằng 0.
C. Hàm số đạt cực tiểu tại \(x = 2\). D. Hàm số đạt cực đại tại \(x = 4\).
Phương pháp giải - Xem chi tiết
Dựa vào bảng biến thiên để xác định các điểm cực trị.
Lời giải chi tiết
Dựa vào bảng biến thiên ta có:
+ Hàm số đạt cực đại tại \(x = 0\) và đạt cực tiểu tại \(x = 2\).
+ Hàm số có giá trị cực đại bằng 4.
Chọn C.
Giải bài 10 trang 12 SBT Toán 12 Cánh Diều: Tổng quan
Bài 10 trang 12 sách bài tập Toán 12 Cánh Diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các công thức đạo hàm cơ bản, quy tắc tính đạo hàm của hàm số hợp, và đạo hàm của hàm số lượng giác để giải quyết các bài toán cụ thể.
Nội dung chi tiết bài 10 trang 12 SBT Toán 12 Cánh Diều
Bài 10 thường bao gồm các dạng bài tập sau:
- Tính đạo hàm của hàm số: Yêu cầu tính đạo hàm của các hàm số đơn thức, đa thức, và hàm số hợp.
- Tìm đạo hàm cấp hai: Tính đạo hàm bậc hai của hàm số đã cho.
- Ứng dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến: Xác định phương trình tiếp tuyến của đồ thị hàm số tại một điểm cho trước.
- Khảo sát hàm số: Sử dụng đạo hàm để xác định khoảng đồng biến, nghịch biến, cực trị của hàm số.
Hướng dẫn giải bài 10 trang 12 SBT Toán 12 Cánh Diều
Để giải bài 10 trang 12 SBT Toán 12 Cánh Diều hiệu quả, học sinh cần:
- Nắm vững các công thức đạo hàm cơ bản: Đạo hàm của hàm số lũy thừa, hàm số lượng giác, hàm số mũ, hàm số logarit.
- Hiểu rõ các quy tắc tính đạo hàm: Quy tắc cộng, trừ, nhân, chia, và quy tắc đạo hàm của hàm số hợp.
- Luyện tập thường xuyên: Giải nhiều bài tập tương tự để rèn luyện kỹ năng và làm quen với các dạng bài khác nhau.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Ví dụ minh họa giải bài 10 trang 12 SBT Toán 12 Cánh Diều
Ví dụ: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải:
f'(x) = 3x2 + 4x - 5
Lưu ý khi giải bài tập về đạo hàm
Khi giải bài tập về đạo hàm, cần chú ý:
- Sử dụng đúng công thức đạo hàm: Lựa chọn công thức đạo hàm phù hợp với từng loại hàm số.
- Áp dụng đúng quy tắc tính đạo hàm: Thực hiện các phép tính đạo hàm theo đúng quy tắc.
- Kiểm tra lại kết quả: Đảm bảo kết quả đạo hàm là chính xác.
Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn là địa chỉ tin cậy cung cấp lời giải chi tiết, chính xác và dễ hiểu cho các bài tập trong sách giáo khoa và sách bài tập Toán 12 Cánh Diều. Chúng tôi cam kết mang đến cho học sinh những tài liệu học tập chất lượng, giúp các em học tập hiệu quả và đạt kết quả cao trong môn Toán.
Bảng tổng hợp công thức đạo hàm cơ bản
| Hàm số | Đạo hàm |
|---|---|
| y = c (c là hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = sin x | y' = cos x |
| y = cos x | y' = -sin x |
Hy vọng với những hướng dẫn chi tiết trên, các em học sinh sẽ tự tin giải quyết bài 10 trang 12 SBT Toán 12 Cánh Diều và các bài tập tương tự. Chúc các em học tập tốt!