Giải bài 1 trang 60 sách bài tập toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 1 trang 60 SBT Toán 12 Cánh Diều
Tusach.vn cung cấp lời giải chi tiết bài 1 trang 60 sách bài tập Toán 12 Cánh Diều, giúp học sinh dễ dàng nắm vững kiến thức và rèn luyện kỹ năng giải bài tập. Bài giải được trình bày rõ ràng, dễ hiểu, kèm theo phương pháp giải và các lưu ý quan trọng.
Chúng tôi luôn cập nhật nhanh chóng và chính xác đáp án các bài tập trong sách bài tập Toán 12 Cánh Diều, hỗ trợ tối đa cho quá trình học tập của bạn.
Cho tứ diện (ABCD). Lấy (G) là trọng tâm tam giác (BCD). Phát biểu nào sau đây là sai? A. (overrightarrow {GB} + overrightarrow {GC} + overrightarrow {GD} = overrightarrow 0 ). B. (overrightarrow {GA} + overrightarrow {GB} + overrightarrow {GC} + overrightarrow {GD} = overrightarrow 0 ). C. (overrightarrow {CB} + overrightarrow {CD} = 3overrightarrow {CG} ). D. (overrightarrow {AB} + overrightarrow {AC} + overrightarrow {AD} = 3overrightarrow {AG} ).
Đề bài
Cho tứ diện \(ABCD\). Lấy \(G\) là trọng tâm tam giác \(BCD\). Phát biểu nào sau đây là sai?
A. \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)
B. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)
C. \(\overrightarrow {CB} + \overrightarrow {CD} = 3\overrightarrow {CG} \)
D. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \).
Phương pháp giải - Xem chi tiết
‒ Sử dụng tính chất trung điểm của đoạn thẳng và tính chất trọng tâm của tam giác.
Lời giải chi tiết
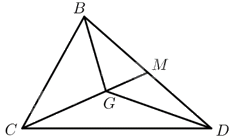
Theo tính chất trọng tâm của tam giác, với \(G\) là trọng tâm tam giác \(BCD\), ta có: \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \). Vậy A đúng.
Gọi \(M\) là trung điểm của \(BD\). Ta có:
\(\overrightarrow {CB} + \overrightarrow {CD} = 2\overrightarrow {CM} = 2.\frac{2}{3}\overrightarrow {CG} = 3\overrightarrow {CG} \). Vậy C đúng.
Ta có: \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = \overrightarrow {AG} + \overrightarrow {GB} + \overrightarrow {AG} + \overrightarrow {GC} + \overrightarrow {AG} + \overrightarrow {GD} = 3\overrightarrow {AG} + \left( {\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} } \right) = 3\overrightarrow {AG} \). Vậy D đúng.
Chọn B.
Giải bài 1 trang 60 SBT Toán 12 Cánh Diều: Tổng quan và hướng dẫn chi tiết
Bài 1 trang 60 sách bài tập Toán 12 Cánh Diều thuộc chương trình học môn Toán lớp 12, tập trung vào việc ôn tập chương 1: Hàm số bậc hai. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về parabol, điều kiện xác định, tập giá trị, và các tính chất của hàm số bậc hai để giải quyết các bài toán cụ thể.
Nội dung bài tập 1 trang 60 SBT Toán 12 Cánh Diều
Thông thường, bài tập 1 trang 60 sẽ bao gồm các dạng bài sau:
- Xác định các hệ số a, b, c của hàm số bậc hai: Yêu cầu học sinh xác định đúng các hệ số này từ phương trình hàm số.
- Tìm đỉnh của parabol: Tính tọa độ đỉnh của parabol dựa trên công thức.
- Xác định trục đối xứng của parabol: Xác định phương trình đường thẳng là trục đối xứng của parabol.
- Tìm tập giá trị của hàm số: Xác định khoảng giá trị mà hàm số có thể đạt được.
- Vẽ đồ thị hàm số: Vẽ đồ thị của hàm số bậc hai trên mặt phẳng tọa độ.
Phương pháp giải bài tập 1 trang 60 SBT Toán 12 Cánh Diều
Để giải quyết hiệu quả bài tập 1 trang 60, học sinh cần nắm vững các kiến thức và kỹ năng sau:
- Nắm vững định nghĩa hàm số bậc hai: Hiểu rõ dạng tổng quát của hàm số bậc hai: y = ax2 + bx + c (a ≠ 0).
- Sử dụng công thức tính đỉnh của parabol: Tọa độ đỉnh I(x0; y0) được tính bằng công thức: x0 = -b/2a và y0 = -Δ/4a (với Δ = b2 - 4ac).
- Áp dụng các tính chất của parabol: Hiểu rõ các tính chất như đối xứng, chiều mở của parabol, và vị trí của đỉnh.
- Sử dụng các phương pháp vẽ đồ thị hàm số: Xác định các điểm đặc biệt (đỉnh, giao điểm với trục tọa độ) để vẽ đồ thị chính xác.
Ví dụ minh họa giải bài 1 trang 60 SBT Toán 12 Cánh Diều
Bài toán: Cho hàm số y = 2x2 - 8x + 6. Tìm đỉnh của parabol và vẽ đồ thị hàm số.
Giải:
- Xác định hệ số: a = 2, b = -8, c = 6.
- Tính đỉnh: x0 = -(-8)/(2*2) = 2; y0 = -((-8)2 - 4*2*6)/(4*2) = -1.
- Vậy đỉnh của parabol là: I(2; -1).
- Vẽ đồ thị: Xác định thêm các điểm đặc biệt như giao điểm với trục Oy (x=0 => y=6) và trục Ox (giải phương trình 2x2 - 8x + 6 = 0).
Lưu ý khi giải bài tập 1 trang 60 SBT Toán 12 Cánh Diều
Để đạt kết quả tốt nhất, học sinh nên:
- Đọc kỹ đề bài và xác định rõ yêu cầu.
- Sử dụng đúng công thức và phương pháp giải.
- Kiểm tra lại kết quả sau khi giải xong.
- Tham khảo các bài giải mẫu và lời giải chi tiết trên tusach.vn.
Tusach.vn – Hỗ trợ học tập môn Toán hiệu quả
Tusach.vn là địa chỉ tin cậy cung cấp lời giải chi tiết, chính xác và dễ hiểu cho các bài tập trong sách giáo khoa và sách bài tập Toán 12 Cánh Diều. Chúng tôi cam kết đồng hành cùng bạn trên con đường chinh phục môn Toán!
| Chương | Bài tập | Liên kết |
|---|---|---|
| 1 | Bài 1 trang 60 | Giải bài 1 trang 60 |
| 1 | Bài 2 trang 60 | Giải bài 2 trang 60 |