Logo

Giải bài 15 trang 67 sách bài tập toán 12 - Cánh diều

Tổng quan nội dung

Giải bài 15 trang 67 SBT Toán 12 Cánh Diều

Tusach.vn xin giới thiệu đến quý độc giả lời giải chi tiết bài 15 trang 67 sách bài tập Toán 12 Cánh Diều. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Chúng tôi luôn cố gắng cung cấp những nội dung chất lượng, chính xác và cập nhật nhất để hỗ trợ học sinh trong quá trình học tập.

Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Trong không gian với hệ toạ độ (Oxyz), cho hình hộp (ABCD.A'B'C'D') có (A'left( {1;0;1} right),)(B'left( {2;1;2} right),D'left( {1; - 1;1} right),Cleft( {4;5; - 5} right)). a) Toạ độ của vectơ (overrightarrow {A'D'} ) là (left( {0; - 1;0} right)). b) Gọi toạ độ của điểm (B) là (left( {{x_B};{y_B};{z_B}} right)), ta có toạ độ của vectơ (overrightarrow {BC} ) là (left( {{x_B} - 4;{y_B} - 5;{z_B

Đề bài

Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).Trong không gian với hệ toạ độ \(Oxyz\), cho hình hộp \(ABCD.A'B'C'D'\) có \(A'\left( {1;0;1} \right),\)\(B'\left( {2;1;2} \right),D'\left( {1; - 1;1} \right),C\left( {4;5; - 5} \right)\). a) Toạ độ của vectơ \(\overrightarrow {A'D'} \) là \(\left( {0; - 1;0} \right)\). b) Gọi toạ độ của điểm \(B\) là \(\left( {{x_B};{y_B};{z_B}} \right)\), ta có toạ độ của vectơ \(\overrightarrow {BC} \) là \(\left( {{x_B} - 4;{y_B} - 5;{z_B} + 5} \right)\). c) Trong hình hộp \(ABCD.A'B'C'D'\), ta có: \(\overrightarrow {BC} = \overrightarrow {A'D'} \). d) Toạ độ điểm \(B\) là \(\left( {4;4; - 5} \right)\).

Phương pháp giải - Xem chi tiếtGiải bài 15 trang 67 sách bài tập toán 12 - Cánh diều 1

‒ Sử dụng toạ độ của vectơ \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\).

‒ Sử dụng tính chất hai vectơ bằng nhau: Với \(\overrightarrow u = \left( {{x_1};{y_1};{z_1}} \right)\) và \(\overrightarrow v = \left( {{x_2};{y_2};{z_2}} \right)\), ta có: \(\overrightarrow u = \overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\\{z_1} = {z_2}\end{array} \right.\).

Lời giải chi tiết

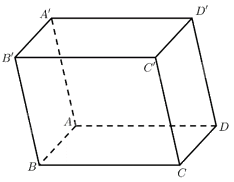
Giải bài 15 trang 67 sách bài tập toán 12 - Cánh diều 2

\(\overrightarrow {A'D'} = \left( {1 - 1; - 1 - 0;1 - 1} \right) = \left( {0; - 1;0} \right)\). Vậy a) đúng.

\(\overrightarrow {BC} = \left( {4 - {x_B};5 - {y_B}; - 5 - {z_B}} \right)\). Vậy b) sai.

\(ABCD.A'B'C'D'\) là hình hộp nên \(\overrightarrow {BC} = \overrightarrow {A'D'} \). Vậy c) đúng.

Ta có: \(\overrightarrow {BC} = \overrightarrow {A'D'} \Leftrightarrow \left\{ \begin{array}{l}4 - {x_B} = 0\\5 - {y_B} = - 1\\ - 5 - {z_B} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 4\\{y_B} = 6\\{z_B} = - 5\end{array} \right.\). Vậy \(B\left( {4;6; - 5} \right)\). Vậy d) sai.

a) Đ

b) S

c) Đ

d) S

Giải bài 15 trang 67 SBT Toán 12 Cánh Diều: Tổng quan

Bài 15 trang 67 sách bài tập Toán 12 Cánh Diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về các chủ đề như đường thẳng và mặt phẳng trong không gian, quan hệ song song, quan hệ vuông góc, và các ứng dụng của chúng. Bài tập này thường yêu cầu học sinh vận dụng các định lý, tính chất đã học để giải quyết các bài toán thực tế.

Nội dung chi tiết bài 15 trang 67 SBT Toán 12 Cánh Diều

Bài 15 bao gồm một số câu hỏi và bài tập khác nhau, được chia thành các phần nhỏ để học sinh dễ dàng tiếp cận và giải quyết. Các dạng bài tập thường gặp bao gồm:

  • Xác định vị trí tương đối giữa đường thẳng và mặt phẳng: Học sinh cần xác định xem một đường thẳng có song song, vuông góc, cắt hoặc nằm trong một mặt phẳng hay không.
  • Tính góc giữa đường thẳng và mặt phẳng: Yêu cầu tính góc giữa một đường thẳng và hình chiếu của nó trên một mặt phẳng.
  • Tính khoảng cách từ một điểm đến mặt phẳng: Tính khoảng cách ngắn nhất từ một điểm đến một mặt phẳng.
  • Chứng minh các quan hệ hình học: Chứng minh các quan hệ song song, vuông góc giữa các đường thẳng và mặt phẳng.

Hướng dẫn giải bài 15 trang 67 SBT Toán 12 Cánh Diều

Để giải bài 15 trang 67 SBT Toán 12 Cánh Diều một cách hiệu quả, học sinh cần:

  1. Nắm vững kiến thức lý thuyết: Hiểu rõ các định lý, tính chất về đường thẳng và mặt phẳng trong không gian.
  2. Đọc kỹ đề bài: Xác định rõ yêu cầu của bài toán và các dữ kiện đã cho.
  3. Vẽ hình minh họa: Vẽ hình minh họa giúp học sinh hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
  4. Sử dụng các công thức và phương pháp phù hợp: Áp dụng các công thức và phương pháp đã học để giải quyết bài toán.
  5. Kiểm tra lại kết quả: Sau khi giải xong, học sinh nên kiểm tra lại kết quả để đảm bảo tính chính xác.

Ví dụ minh họa giải bài 15 trang 67 SBT Toán 12 Cánh Diều

Bài tập: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).

Giải:

  1. Gọi H là hình chiếu của S lên mặt phẳng (ABCD). Vì SA vuông góc với (ABCD) nên H trùng với A.
  2. Trong mặt phẳng (ABCD), gọi AC là đường chéo của hình vuông ABCD. Ta có AC = a√2.
  3. Xét tam giác SAC vuông tại A, ta có tan góc SCA = SA/AC = a/(a√2) = 1/√2.
  4. Vậy góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng góc SCA, và tan góc SCA = 1/√2.

Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín

Tusach.vn là một website cung cấp tài liệu học tập Toán 12 uy tín, chất lượng. Chúng tôi cung cấp đầy đủ các giải bài tập, đáp án, lý thuyết và các bài giảng video giúp học sinh học Toán 12 một cách hiệu quả nhất. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!

Bảng tổng hợp các bài giải Toán 12 Cánh Diều

ChươngBàiTrangLink
1110Link bài 1
1215Link bài 2
............