Giải bài 54 trang 24 sách bài tập toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 54 trang 24 SBT Toán 12 Cánh Diều
Bài 54 trang 24 sách bài tập Toán 12 Cánh Diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập Toán 12.
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ { - 2} \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: Khẳng định nào sau đây là đúng? A. Đồ thị hàm số có tiệm cận đứng là đường thẳng \(y = 2\) và tiệm cận ngang là đường thẳng \(x = - 2\). B. Đồ thị hàm số có tiệm cận đứng là đường thẳng \(y = - 2\) và tiệm cận ngang là đường thẳng \(x = 2\). C. Đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = 2\) và tiệm cận ngang là đường
Đề bài
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ { - 2} \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
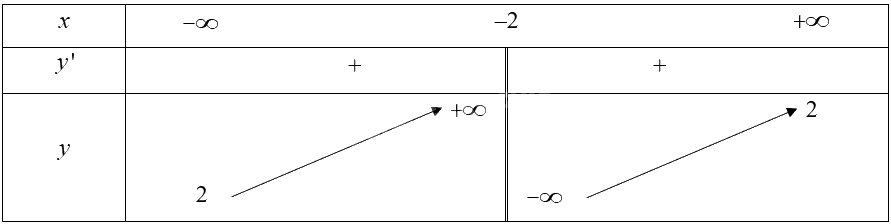
Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số có tiệm cận đứng là đường thẳng \(y = 2\) và tiệm cận ngang là đường thẳng \(x = - 2\).
B. Đồ thị hàm số có tiệm cận đứng là đường thẳng \(y = - 2\) và tiệm cận ngang là đường thẳng \(x = 2\).
C. Đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = 2\) và tiệm cận ngang là đường thẳng \(y = - 2\).
D. Đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = - 2\) và tiệm cận ngang là đường thẳng \(y = 2\).
Phương pháp giải - Xem chi tiết
‒ Tìm tiệm cận đứng: Tính \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right)\) hoặc \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right)\), nếu một trong các giới hạn sau thoả mãn: \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = - \infty ;\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = - \infty \)
thì đường thẳng \(x = {x_0}\) là đường tiệm cận đứng.
‒ Tìm tiệm cận ngang: Nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\) thì đường thẳng \(y = {y_0}\) là đường tiệm cận ngang.
Lời giải chi tiết
Dựa vào bảng biến thiên ta có:
• \(\mathop {\lim }\limits_{x \to - {2^ - }} f\left( x \right) = + \infty \).
Vậy \(x = - 2\) là tiệm cận đứng của đồ thị hàm số đã cho.
• \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2;\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2\).
Vậy \(y = 2\) là tiệm cận ngang của đồ thị hàm số đã cho.
Chọn D.
Giải bài 54 trang 24 SBT Toán 12 Cánh Diều: Tổng quan và Phương pháp giải
Bài 54 trang 24 sách bài tập Toán 12 Cánh Diều thuộc chương trình học về đạo hàm của hàm số. Bài tập này thường yêu cầu học sinh:
- Tính đạo hàm của hàm số.
- Tìm cực trị của hàm số.
- Khảo sát hàm số.
- Ứng dụng đạo hàm để giải quyết các bài toán thực tế.
Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
- Định nghĩa đạo hàm.
- Các quy tắc tính đạo hàm.
- Ứng dụng của đạo hàm.
Lời giải chi tiết bài 54 trang 24 SBT Toán 12 Cánh Diều
Dưới đây là lời giải chi tiết cho bài 54 trang 24 SBT Toán 12 Cánh Diều. (Lưu ý: Nội dung lời giải cụ thể sẽ phụ thuộc vào đề bài của bài 54. Ví dụ sau chỉ mang tính minh họa)
Ví dụ minh họa (Giả sử bài 54 yêu cầu tìm cực trị của hàm số f(x) = x^3 - 3x^2 + 2):
- Bước 1: Tính đạo hàm f'(x)
- Bước 2: Tìm các điểm dừng (f'(x) = 0)
- Bước 3: Lập bảng biến thiên
- Bước 4: Kết luận
f'(x) = 3x^2 - 6x
3x^2 - 6x = 0 => 3x(x - 2) = 0 => x = 0 hoặc x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | ↗ | ↘ | ↗ |
Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2. Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Mẹo giải bài tập đạo hàm Toán 12
Để giải bài tập đạo hàm một cách nhanh chóng và chính xác, bạn có thể áp dụng một số mẹo sau:
- Nắm vững các quy tắc tính đạo hàm cơ bản.
- Sử dụng bảng đạo hàm để tra cứu nhanh chóng.
- Phân tích kỹ đề bài để xác định phương pháp giải phù hợp.
- Kiểm tra lại kết quả sau khi giải xong.
Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn là một website cung cấp đầy đủ các tài liệu học tập Toán 12, bao gồm:
- Giải bài tập sách giáo khoa.
- Giải bài tập sách bài tập.
- Đề thi thử Toán 12.
- Các bài viết hướng dẫn giải bài tập.
Hãy truy cập Tusach.vn ngay hôm nay để học tốt môn Toán 12!