Giải bài 73 trang 36 SBT Toán 12 Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết bài 73 trang 36 sách bài tập Toán 12 Cánh Diều. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết từng bước để giúp các em hiểu rõ hơn về nội dung bài học.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.
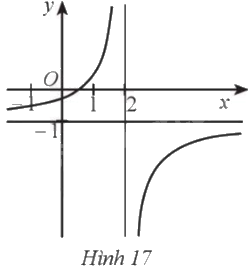
Đường cong ở Hình 17 là đồ thị của hàm số:
A. \(y = \frac{{1 - 2{\rm{x}}}}{{2{\rm{x}} - 4}}\).
B. \(y = \frac{{1 - {\rm{x}}}}{{{\rm{x}} - 2}}\).
C. \(y = \frac{{1 - {\rm{x}}}}{{2 - x}}\).
D. \(y = \frac{{1 - 2{\rm{x}}}}{{x - 1}}\).
Giải bài 73 trang 36 SBT Toán 12 Cánh Diều: Tổng quan
Bài 73 trang 36 sách bài tập Toán 12 Cánh Diều thuộc chương trình học về Đường thẳng và mặt phẳng trong không gian. Bài tập này tập trung vào việc rèn luyện kỹ năng xác định vị trí tương đối giữa đường thẳng và mặt phẳng, sử dụng các định lý và tính chất đã học để giải quyết các bài toán thực tế.
Nội dung chi tiết bài 73 trang 36 SBT Toán 12 Cánh Diều
Bài 73 bao gồm các dạng bài tập sau:
- Dạng 1: Xác định vị trí tương đối giữa đường thẳng và mặt phẳng.
- Dạng 2: Tính góc giữa đường thẳng và mặt phẳng.
- Dạng 3: Tìm giao điểm của đường thẳng và mặt phẳng.
Lời giải chi tiết bài 73 trang 36 SBT Toán 12 Cánh Diều
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 73:
Câu 1: (Trích dẫn câu hỏi từ SBT)
(Giả sử câu hỏi là: Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh BC. Chứng minh rằng AM song song với mặt phẳng (SCD).)
Lời giải:
- Gọi N là trung điểm của cạnh CD.
- Chứng minh MN song song với SD (sử dụng tính chất đường trung bình của tam giác BCD).
- Vì MN song song với SD và MN nằm trong mặt phẳng (AMN), SD nằm trong mặt phẳng (SCD) nên AM song song với mặt phẳng (SCD) (theo dấu hiệu nhận biết đường thẳng song song với mặt phẳng).
Câu 2: (Trích dẫn câu hỏi từ SBT)
(Giả sử câu hỏi là: Tính góc giữa đường thẳng SA và mặt phẳng (ABCD) của hình chóp S.ABCD.)
Lời giải:
Để tính góc giữa đường thẳng SA và mặt phẳng (ABCD), ta thực hiện các bước sau:
- Kẻ AH vuông góc với BC tại H.
- Kẻ AK vuông góc với AH tại K.
- Khi đó, AK là hình chiếu vuông góc của SA lên mặt phẳng (ABCD).
- Góc giữa SA và mặt phẳng (ABCD) là góc SAH.
- Sử dụng các công thức lượng giác và thông tin đã cho để tính góc SAH.
Mẹo giải bài tập về đường thẳng và mặt phẳng
Để giải tốt các bài tập về đường thẳng và mặt phẳng, các em cần nắm vững các kiến thức sau:
- Các định lý về quan hệ song song giữa đường thẳng và mặt phẳng.
- Các định lý về quan hệ vuông góc giữa đường thẳng và mặt phẳng.
- Cách xác định góc giữa đường thẳng và mặt phẳng.
- Cách tìm giao điểm của đường thẳng và mặt phẳng.
Tài liệu tham khảo hữu ích
Ngoài sách giáo khoa và sách bài tập, các em có thể tham khảo thêm các tài liệu sau:
- Các bài giảng trực tuyến về hình học không gian.
- Các trang web và diễn đàn học tập trực tuyến.
- Các bài tập trắc nghiệm và bài tập tự luyện.
Kết luận
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em sẽ hiểu rõ hơn về bài 73 trang 36 SBT Toán 12 Cánh Diều và tự tin giải quyết các bài tập tương tự. Chúc các em học tập tốt!
Tusach.vn – Luôn đồng hành cùng các em trên con đường chinh phục tri thức.
