Giải bài 4 trang 11 sách bài tập toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 4 trang 11 SBT Toán 12 Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 4 trang 11 sách bài tập Toán 12 Cánh Diều. Bài giải này được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp những tài liệu học tập chất lượng nhất, hỗ trợ học sinh học tập hiệu quả.
Cho hàm số \(y = - {x^3} + 3{x^2} - 4\). Mệnh đề nào dưới đây là đúng?
Đề bài
Cho hàm số \(y = - {x^3} + 3{x^2} - 4\). Mệnh đề nào dưới đây là đúng?
A. Hàm số đồng biến trên khoảng \(\left( {0;2} \right)\).
B. Hàm số nghịch biến trên khoảng \(\left( { - \infty ;2} \right)\).
C. Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\).
D. Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\).
Phương pháp giải - Xem chi tiết
Các bước để tìm khoảng đồng biến, nghịch biến của hàm số \(f\left( x \right)\):
Bước 1. Tìm tập xác định của hàm số \(y = f\left( x \right)\).
Bước 2. Tính đạo hàm \(f'\left( x \right)\). Tìm các điểm \({x_i}\left( {i = 1,2,...,n} \right)\) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.
Bước 3. Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4. Căn cứ vào bảng biến thiên, nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết
Hàm số có tập xác định là \(\mathbb{R}\).
Ta có:
\({y^\prime } = - 3{{\rm{x}}^2} + 6{\rm{x}}\)
\(y' = 0\) khi \(x = 0\) hoặc \(x = 2\).
Bảng biến thiên của hàm số:
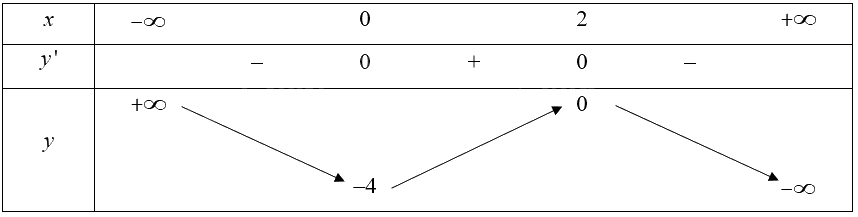
Vậy hàm số đồng biến trên khoảng \(\left( {0;2} \right)\); nghịch biến trên mỗi khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\).
Chọn A.
Giải bài 4 trang 11 SBT Toán 12 Cánh Diều: Chi tiết và Dễ Hiểu
Bài 4 trang 11 sách bài tập Toán 12 Cánh Diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập chương 1: Hàm số bậc hai. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về parabol, điều kiện xác định, và các tính chất của hàm số bậc hai để giải quyết các bài toán cụ thể.
Nội dung bài 4 trang 11 SBT Toán 12 Cánh Diều
Bài 4 thường bao gồm các dạng bài tập sau:
- Xác định các yếu tố của parabol: Tìm đỉnh, trục đối xứng, tiêu điểm, đường chuẩn của parabol.
- Viết phương trình parabol: Viết phương trình parabol khi biết các yếu tố hoặc thông tin liên quan.
- Ứng dụng của parabol: Giải các bài toán thực tế liên quan đến parabol, ví dụ như tìm quỹ đạo của vật thể ném lên.
- Khảo sát hàm số bậc hai: Xác định khoảng đồng biến, nghịch biến, cực trị của hàm số bậc hai.
Lời giải chi tiết bài 4 trang 11 SBT Toán 12 Cánh Diều
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 4 trang 11 SBT Toán 12 Cánh Diều, chúng tôi xin trình bày lời giải chi tiết như sau:
Ví dụ minh họa (Giả định nội dung bài 4):
Bài 4: Cho parabol (P): y2 = 8x. Tìm tọa độ tiêu điểm và phương trình đường chuẩn của (P).
Lời giải:
- Xác định các yếu tố của parabol:
- 4p = 8 => p = 2
- Tiêu điểm: F(p; 0) = F(2; 0)
- Đường chuẩn: x = -p => x = -2
- Kết luận: Tiêu điểm của parabol (P) là F(2; 0) và phương trình đường chuẩn là x = -2.
Mẹo giải bài tập về parabol
Để giải tốt các bài tập về parabol, các em cần nắm vững các kiến thức sau:
- Công thức: Nắm vững công thức của parabol, tiêu điểm, đường chuẩn, trục đối xứng.
- Hình vẽ: Vẽ hình parabol để dễ dàng hình dung và tìm ra lời giải.
- Phân tích: Phân tích kỹ đề bài để xác định các yếu tố đã cho và yêu cầu của bài toán.
- Luyện tập: Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Tusach.vn – Đồng hành cùng học sinh
Tusach.vn là website cung cấp lời giải bài tập Toán 12, cùng với nhiều tài liệu học tập hữu ích khác. Chúng tôi luôn cập nhật những lời giải mới nhất, chính xác nhất, giúp các em học sinh học tập hiệu quả.
Ngoài ra, Tusach.vn còn cung cấp các bài giảng video, bài tập trắc nghiệm, và các tài liệu ôn thi THPT Quốc gia. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
Hy vọng với lời giải chi tiết và những chia sẻ trên, các em học sinh sẽ tự tin hơn khi giải bài 4 trang 11 SBT Toán 12 Cánh Diều và đạt kết quả tốt trong môn Toán.