Giải bài 26 trang 17 sách bài tập toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 26 trang 17 SBT Toán 12 Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 26 trang 17 sách bài tập Toán 12 Cánh Diều. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác đáp án các bài tập trong SBT Toán 12 Cánh Diều.
Giá trị nhỏ nhất của hàm số (y = sqrt {{x^2} + 4} ) bằng: A. 2. B. 4. C. 0. D. 1.
Đề bài
Giá trị nhỏ nhất của hàm số \(y = \sqrt {{x^2} + 4} \) bằng:
A. 2.
B. 4.
C. 0.
D. 1.
Phương pháp giải - Xem chi tiết
Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng, đoạn hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
Lời giải chi tiết
Hàm số có tập xác định là \(\mathbb{R}\).
Ta có: \({y^\prime } = \frac{{{{\left( {{x^2} + 4} \right)}^\prime }}}{{2\sqrt {{x^2} + 4} }} = \frac{{2{\rm{x}}}}{{2\sqrt {{x^2} + 4} }} = \frac{{\rm{x}}}{{\sqrt {{x^2} + 4} }}\)
\(y' = 0\) khi \(x = 0\).
Bảng biến thiên của hàm số:
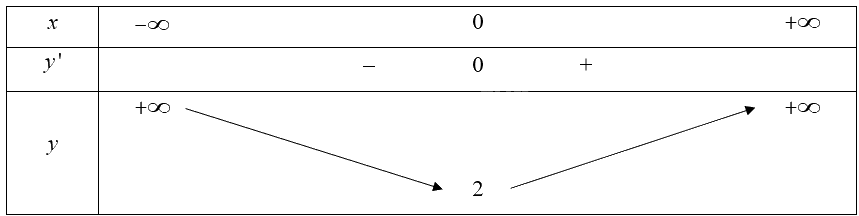
Căn cứ vào bảng biến thiên, ta có: \(\min f\left( x \right) = 2\) tại \({\rm{x}} = 0\).
Chọn A.
Giải bài 26 trang 17 SBT Toán 12 Cánh Diều: Tổng quan và Phương pháp giải
Bài 26 trang 17 sách bài tập Toán 12 Cánh Diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về các chủ đề như đường thẳng và mặt phẳng trong không gian, quan hệ song song, quan hệ vuông góc, và các bài toán liên quan đến khoảng cách. Việc nắm vững kiến thức nền tảng và phương pháp giải là yếu tố then chốt để giải quyết thành công bài tập này.
Nội dung chi tiết bài 26 trang 17 SBT Toán 12 Cánh Diều
Bài 26 bao gồm các dạng bài tập khác nhau, yêu cầu học sinh vận dụng kiến thức đã học để:
- Xác định vị trí tương đối giữa đường thẳng và mặt phẳng.
- Tính góc giữa đường thẳng và mặt phẳng.
- Tính khoảng cách từ một điểm đến mặt phẳng.
- Giải các bài toán thực tế liên quan đến ứng dụng của đường thẳng và mặt phẳng.
Lời giải chi tiết từng phần của bài 26 trang 17 SBT Toán 12 Cánh Diều
Câu a: (Ví dụ minh họa)
Để giải câu a, ta cần xác định phương trình mặt phẳng chứa đường thẳng d và điểm A. Sau đó, tính khoảng cách từ điểm B đến mặt phẳng này. Lưu ý sử dụng công thức tính khoảng cách từ một điểm đến một mặt phẳng: d = |Ax0 + By0 + Cz0 + D| / √(A2 + B2 + C2).
Câu b: (Ví dụ minh họa)
Đối với câu b, ta cần tìm giao điểm của đường thẳng d và mặt phẳng (P). Sau đó, sử dụng công thức tính góc giữa đường thẳng và mặt phẳng: sin(θ) = |a1A + a2B + a3C| / √(a12 + a22 + a32)√(A2 + B2 + C2).
Phương pháp giải bài tập về đường thẳng và mặt phẳng trong không gian
- Nắm vững kiến thức lý thuyết: Hiểu rõ các định nghĩa, định lý, công thức liên quan đến đường thẳng và mặt phẳng.
- Xác định đúng các yếu tố cần thiết: Xác định phương trình đường thẳng, phương trình mặt phẳng, tọa độ các điểm, vector chỉ phương, vector pháp tuyến.
- Vận dụng linh hoạt các công thức: Sử dụng các công thức tính khoảng cách, góc, vị trí tương đối một cách chính xác.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Mẹo giải nhanh bài tập Toán 12
Để giải nhanh các bài tập Toán 12, bạn có thể áp dụng một số mẹo sau:
- Sử dụng các công thức tính nhanh.
- Phân tích bài toán một cách logic.
- Vẽ hình minh họa để dễ hình dung.
- Luyện tập thường xuyên để làm quen với các dạng bài tập.
Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn là một website cung cấp tài liệu học tập Toán 12 uy tín, chất lượng. Chúng tôi cung cấp đầy đủ đáp án, lời giải chi tiết các bài tập trong sách giáo khoa, sách bài tập, đề thi thử. Hãy truy cập Tusach.vn để học tập và ôn luyện hiệu quả!
Bảng tổng hợp các công thức quan trọng
| Công thức | Mô tả |
|---|---|
| Khoảng cách từ điểm M(x0, y0, z0) đến mặt phẳng (P): Ax + By + Cz + D = 0 | d = |Ax0 + By0 + Cz0 + D| / √(A2 + B2 + C2) |
| Góc giữa đường thẳng d và mặt phẳng (P) | sin(θ) = |a1A + a2B + a3C| / √(a12 + a22 + a32)√(A2 + B2 + C2) |
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên đây, các bạn học sinh sẽ tự tin hơn trong việc giải bài 26 trang 17 SBT Toán 12 Cánh Diều và đạt kết quả tốt trong môn Toán.