Giải bài 27 trang 17 sách bài tập toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 27 trang 17 SBT Toán 12 Cánh Diều
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho bài tập 27 trang 17 sách bài tập Toán 12 Cánh Diều. Chúng tôi hiểu rằng việc giải bài tập có thể gặp nhiều khó khăn, vì vậy chúng tôi đã biên soạn hướng dẫn này để giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Bài viết này sẽ cung cấp đáp án, phương pháp giải và những lưu ý quan trọng để bạn có thể hoàn thành bài tập một cách hiệu quả nhất.
Giá trị lớn nhất của hàm số (y = frac{{2{rm{x}} - 1}}{{x - 2}}) trên nửa khoảng (left[ { - 3;2} right)) bằng: A. ( - frac{7}{5}). B. 7. C. (frac{7}{5}). D. ‒7.
Đề bài
Giá trị lớn nhất của hàm số \(y = \frac{{2{\rm{x}} - 1}}{{x - 2}}\) trên nửa khoảng \(\left[ { - 3;2} \right)\) bằng:
A. \( - \frac{7}{5}\).
B. 7.
C. \(\frac{7}{5}\).
D. ‒7.
Phương pháp giải - Xem chi tiết
Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng, đoạn hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
Lời giải chi tiết
Xét hàm số \(y = \frac{{2{\rm{x}} - 1}}{{x - 2}}\) trên nửa khoảng \(\left[ { - 3;2} \right)\).
Ta có:
\({y^\prime } = \frac{{ - 3}}{{{{\left( {x - 2} \right)}^2}}} < 0,\forall x \ne 2\)
Bảng biến thiên của hàm số:
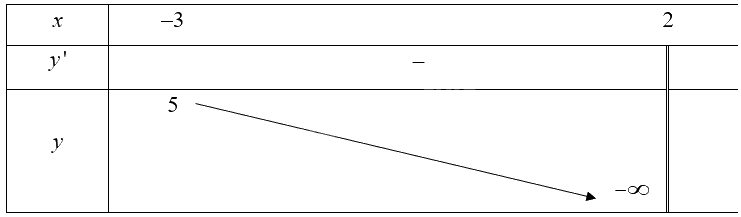
Căn cứ vào bảng biến thiên, ta có: \(\mathop {\max }\limits_{\left[ { - 3;2} \right)} f\left( x \right) = \frac{7}{5}\) tại \({\rm{x}} = - 3\).
Chọn C.
Giải bài 27 trang 17 SBT Toán 12 Cánh Diều: Tổng quan và Hướng dẫn chi tiết
Bài 27 trang 17 sách bài tập Toán 12 Cánh Diều thuộc chương trình học về Đạo hàm của hàm số hợp. Bài tập này thường yêu cầu học sinh vận dụng các quy tắc đạo hàm, đặc biệt là quy tắc đạo hàm hàm hợp, để tính đạo hàm của các hàm số phức tạp. Việc nắm vững quy tắc này là vô cùng quan trọng để giải quyết các bài toán liên quan đến đạo hàm trong chương trình Toán 12.
Nội dung bài tập 27 trang 17 SBT Toán 12 Cánh Diều
Bài tập 27 thường bao gồm các dạng bài sau:
- Tính đạo hàm của hàm hợp: Yêu cầu tính đạo hàm của hàm số có dạng y = f(g(x)), y = f(x)^n, v.v.
- Áp dụng quy tắc đạo hàm hàm hợp: Sử dụng quy tắc đạo hàm hàm hợp để giải các bài toán thực tế.
- Tìm đạo hàm cấp hai: Tính đạo hàm bậc hai của hàm số sau khi đã tìm được đạo hàm bậc nhất.
Đáp án và Phương pháp giải chi tiết
Dưới đây là đáp án và phương pháp giải chi tiết cho từng phần của bài tập 27 trang 17 SBT Toán 12 Cánh Diều:
Câu a)
Đề bài: (Ví dụ) Tính đạo hàm của hàm số y = sin(x^2 + 1)
Giải:
- Đặt u = x^2 + 1
- Khi đó, y = sin(u)
- Tính đạo hàm của u theo x: du/dx = 2x
- Tính đạo hàm của y theo u: dy/du = cos(u)
- Áp dụng quy tắc đạo hàm hàm hợp: dy/dx = (dy/du) * (du/dx) = cos(u) * 2x = 2x * cos(x^2 + 1)
Câu b)
Đề bài: (Ví dụ) Tính đạo hàm của hàm số y = (x^3 - 2x)^5
Giải:
- Đặt u = x^3 - 2x
- Khi đó, y = u^5
- Tính đạo hàm của u theo x: du/dx = 3x^2 - 2
- Tính đạo hàm của y theo u: dy/du = 5u^4
- Áp dụng quy tắc đạo hàm hàm hợp: dy/dx = (dy/du) * (du/dx) = 5u^4 * (3x^2 - 2) = 5(x^3 - 2x)^4 * (3x^2 - 2)
Lưu ý khi giải bài tập 27 trang 17 SBT Toán 12 Cánh Diều
- Nắm vững quy tắc đạo hàm hàm hợp: Đây là chìa khóa để giải quyết các bài toán trong bài tập này.
- Xác định đúng hàm trong và hàm ngoài: Việc xác định đúng hàm trong và hàm ngoài sẽ giúp bạn áp dụng quy tắc đạo hàm hàm hợp một cách chính xác.
- Kiểm tra lại kết quả: Sau khi tính đạo hàm, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tusach.vn – Hỗ trợ học tập Toán 12 hiệu quả
Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán 12. Chúng tôi cung cấp đầy đủ đáp án, phương pháp giải chi tiết và các bài tập tương tự để bạn có thể luyện tập và nâng cao kiến thức. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
Bảng tổng hợp các công thức đạo hàm thường dùng
| Công thức | Mô tả |
|---|---|
| (u^n)' = n*u^(n-1)*u' | Đạo hàm của hàm lũy thừa |
| (sin u)' = cos u * u' | Đạo hàm của hàm sin |
| (cos u)' = -sin u * u' | Đạo hàm của hàm cos |