Đề bài
Khi điều tra độ tuổi của dân cư trong một khu phố (đơn vị: tuổi) được kết quả cho bởi Bảng 9.
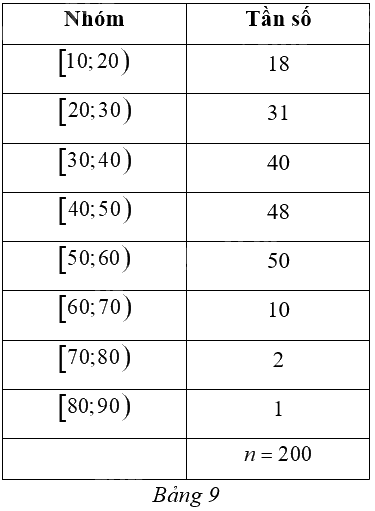
a) Khoảng biến thiên của mẫu số liệu ghép nhóm đó là: \(R = 90\) (tuổi).
b) Nhóm 3 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{4} = \frac{{200}}{4} = 50\).
c) \({Q_3} = 52\frac{{17}}{{24}}\).
d) Khoảng tứ phân vị của mẫu số liệu lớn hơn 20.
Phương pháp giải - Xem chi tiết
‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} - {a_1}\).
‒ Sử dụng công thức tính các tứ phân vị của mẫu số liệu ghép nhóm:
+ Nhóm thứ \(p\) là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{4}\) (tức là \(c{f_{p - 1}} < \frac{n}{4}\) nhưng \(c{f_p} \ge \frac{n}{4}\)). Ta gọi \(s,h,{n_p}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm \(p\), \(c{f_{p - 1}}\) là tần số tích luỹ của nhóm thứ \(p - 1\). Khi đó: \({Q_1} = s + \left( {\frac{{\frac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right).h\).
+ Nhóm thứ \(q\) là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{{3n}}{4}\) (tức là \(c{f_{q - 1}} < \frac{{3n}}{4}\) nhưng \(c{f_q} \ge \frac{{3n}}{4}\)). Ta gọi \(t,l,{n_q}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm \(q\), \(c{f_{q - 1}}\) là tần số tích luỹ của nhóm thứ \(q - 1\). Khi đó: \({Q_3} = t + \left( {\frac{{\frac{{3n}}{4} - c{f_{q - 1}}}}{{{n_q}}}} \right).l\).
‒ Sử dụng công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm: \(\Delta Q = {Q_3} - {Q_1}\).
Lời giải chi tiết
Khoảng biến thiên của mẫu số liệu ghép nhóm đó là: \(R = 90 - 10 = 80\). Vậy a) sai.
Ta có bảng sau:
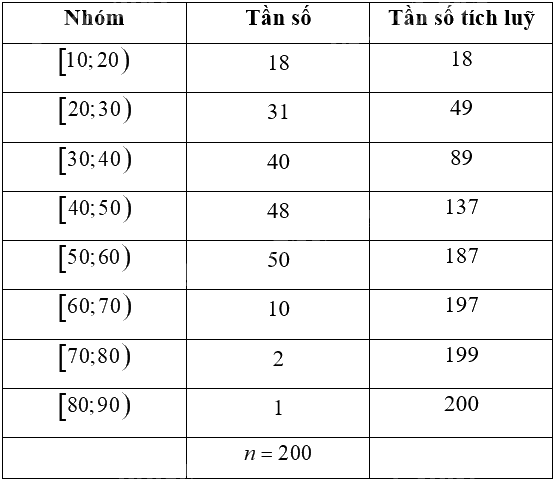
Nhóm 3 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{4} = \frac{{200}}{4} = 50\). Vậy b) đúng.
Nhóm 3 có đầu mút trái \(s = 30\), độ dài \(h = 10\), tần số của nhóm \({n_3} = 40\) và nhóm 2 có tần số tích luỹ \(c{f_2} = 49\).
Ta có: \({Q_1} = s + \left( {\frac{{50 - c{f_2}}}{{{n_3}}}} \right).h = 30 + \left( {\frac{{50 - 49}}{{40}}} \right).10 = 30,25\) (tuổi).
Nhóm 5 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{{3n}}{4} = \frac{{3.200}}{4} = 150\).
Nhóm 5 có đầu mút trái \(t = 50\), độ dài \(l = 10\), tần số của nhóm \({n_5} = 50\) và nhóm 4 có tần số tích luỹ \(c{f_4} = 137\).
Ta có: \({Q_3} = t + \left( {\frac{{150 - c{f_4}}}{{{n_5}}}} \right).l = 50 + \left( {\frac{{150 - 137}}{{50}}} \right).10 = 52,6\) (tuổi). Vậy c) sai.
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \(\Delta Q = {Q_3} - {Q_1} = 52,6 - 30,25 = 22,35 > 20\). Vậy d) đúng.
a) S.
b) Đ.
c) S.
d) Đ.
