Giải bài 56 trang 25 SBT Toán 12 Cánh Diều

Giải bài 56 trang 25 sách bài tập toán 12 - Cánh diều

Tusach.vn xin giới thiệu đáp án chi tiết bài 56 trang 25 sách bài tập Toán 12 Cánh Diều. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Chúng tôi luôn cập nhật nhanh chóng và chính xác các bài giải SBT Toán 12 Cánh Diều, đảm bảo hỗ trợ tối đa cho quá trình học tập của bạn.

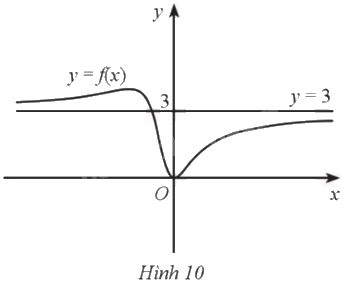
Cho hàm số (y = fleft( x right)) liên tục trên (mathbb{R}) và đồ thị có đường tiệm cận ngang như Hình 10. Hàm số (y = fleft( x right)) có thể là hàm số nào trong các hàm số sau? A. (fleft( x right) = frac{{3{{rm{x}}^2}}}{{{x^2} + x + 1}}). B. (fleft( x right) = frac{{2{{rm{x}}^2}}}{{{x^2} + x + 1}}). C. (fleft( x right) = frac{{{{rm{x}}^2}}}{{{x^2} + x + 1}}). D. (fleft( x right) = frac{{{{rm{x}}^2}}}{{3{x^2} + x + 1}}).

Đề bài

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và đồ thị có đường tiệm cận ngang như Hình 10. Hàm số \(y = f\left( x \right)\) có thể là hàm số nào trong các hàm số sau?

A. \(f\left( x \right) = \frac{{3{{\rm{x}}^2}}}{{{x^2} + x + 1}}\).

B. \(f\left( x \right) = \frac{{2{{\rm{x}}^2}}}{{{x^2} + x + 1}}\).

C. \(f\left( x \right) = \frac{{{{\rm{x}}^2}}}{{{x^2} + x + 1}}\).

D. \(f\left( x \right) = \frac{{{{\rm{x}}^2}}}{{3{x^2} + x + 1}}\).

Giải bài 56 trang 25 sách bài tập toán 12 - Cánh diều 1

Phương pháp giải - Xem chi tiết Giải bài 56 trang 25 sách bài tập toán 12 - Cánh diều 2

‒ Tìm tiệm cận ngang: Nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\) thì đường thẳng \(y = {y_0}\) là đường tiệm cận ngang.

Lời giải chi tiết

Dựa vào đồ thị hàm số ta có \(y = 3\) là đường tiệm cận ngang.

Xét hàm số: \(f\left( x \right) = \frac{{3{{\rm{x}}^2}}}{{{x^2} + x + 1}}\). Ta có:

\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{3{{\rm{x}}^2}}}{{{x^2} + x + 1}} = 3;\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{{3{{\rm{x}}^2}}}{{{x^2} + x + 1}} = 3\).

Vậy \(y = 3\) là tiệm cận ngang của đồ thị hàm số \(f\left( x \right) = \frac{{3{{\rm{x}}^2}}}{{{x^2} + x + 1}}\).

Chọn A.

Giải bài 56 trang 25 SBT Toán 12 Cánh Diều: Tổng quan và Phương pháp giải

Bài 56 trang 25 sách bài tập Toán 12 Cánh Diều thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.

Nội dung chi tiết bài 56 trang 25 SBT Toán 12 Cánh Diều

Để giải quyết bài 56 trang 25 SBT Toán 12 Cánh Diều một cách hiệu quả, bạn cần thực hiện các bước sau:

Đọc kỹ đề bài: Xác định rõ yêu cầu của bài toán, các dữ kiện đã cho và những điều cần tìm.
Xác định hàm số: Nếu bài toán cho một tình huống thực tế, bạn cần xây dựng hàm số mô tả tình huống đó.
Tính đạo hàm: Sử dụng các quy tắc tính đạo hàm để tìm đạo hàm của hàm số.
Giải phương trình đạo hàm: Giải phương trình đạo hàm bằng 0 để tìm các điểm cực trị của hàm số.
Xác định khoảng đơn điệu: Dựa vào dấu của đạo hàm để xác định khoảng đồng biến và nghịch biến của hàm số.
Kết luận: Trả lời câu hỏi của bài toán dựa trên kết quả đã tìm được.

Đáp án chi tiết bài 56 trang 25 SBT Toán 12 Cánh Diều

Dưới đây là đáp án chi tiết cho bài 56 trang 25 SBT Toán 12 Cánh Diều. (Lưu ý: Đáp án cụ thể sẽ phụ thuộc vào nội dung từng câu hỏi trong bài 56. Ví dụ minh họa:)

Ví dụ minh họa (Giả sử bài 56 là bài toán về tối ưu hóa):

Đề bài: Một người nông dân muốn xây dựng một chuồng trại hình chữ nhật có diện tích 100m². Hỏi chu vi của chuồng trại nhỏ nhất có thể là bao nhiêu?

Giải:

Gọi chiều dài và chiều rộng của chuồng trại lần lượt là x và y.
Diện tích chuồng trại là xy = 100.
Chu vi chuồng trại là P = 2(x + y).
Từ xy = 100, ta có y = 100/x.
Thay y = 100/x vào P = 2(x + y), ta được P = 2(x + 100/x).
Tính đạo hàm của P theo x: P' = 2(1 - 100/x²).
Giải phương trình P' = 0, ta được x = 10.
Khi x = 10, y = 100/10 = 10.
Vậy chu vi nhỏ nhất của chuồng trại là P = 2(10 + 10) = 40m.

Mẹo giải bài tập Toán 12 Cánh Diều hiệu quả

Để giải các bài tập Toán 12 Cánh Diều một cách hiệu quả, bạn nên:

Nắm vững kiến thức cơ bản về đạo hàm, tích phân, hàm số, phương trình, bất phương trình.
Luyện tập thường xuyên các bài tập trong sách giáo khoa và sách bài tập.
Sử dụng các công cụ hỗ trợ giải toán như máy tính bỏ túi, phần mềm toán học.
Tham khảo các bài giải chi tiết trên các trang web uy tín như tusach.vn.

Tại sao nên chọn tusach.vn để giải bài tập Toán 12 Cánh Diều?

Tusach.vn là một trang web uy tín, cung cấp các bài giải chi tiết, chính xác và dễ hiểu cho các bài tập Toán 12 Cánh Diều. Chúng tôi có đội ngũ giáo viên giàu kinh nghiệm, luôn cập nhật nhanh chóng các bài giải mới nhất. Ngoài ra, tusach.vn còn cung cấp nhiều tài liệu học tập hữu ích khác như lý thuyết, công thức, bài tập trắc nghiệm,...

Hãy truy cập tusach.vn ngay hôm nay để học tốt môn Toán!