Giải bài 8 trang 61 SBT Toán 12 Cánh Diều

Giải bài 8 trang 61 sách bài tập toán 12 - Cánh diều

Giải bài 8 trang 61 SBT Toán 12 Cánh Diều

Tusach.vn xin giới thiệu lời giải chi tiết bài 8 trang 61 sách bài tập Toán 12 Cánh Diều. Bài giải này được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Chúng tôi luôn cố gắng cung cấp những tài liệu học tập chất lượng nhất, hỗ trợ học sinh học tập hiệu quả.

Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Cho hình chóp tứ giác đều (S.ABCD) có độ dài tất cả các cạnh đều bằng (a) (Hình 10). a) Tứ giác (ABCD) là hình vuông. b) Tam giác (SAC) vuông cân tại (S). c) (left( {overrightarrow {SA} ,overrightarrow {AC} } right) = {45^ circ }). d) (overrightarrow {SA} .overrightarrow {AC} = - {a^2}).

Đề bài

Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).Cho hình chóp tứ giác đều \(S.ABCD\) có độ dài tất cả các cạnh đều bằng \(a\) (Hình 10). a) Tứ giác \(ABCD\) là hình vuông. b) Tam giác \(SAC\) vuông cân tại \(S\). c) \(\left( {\overrightarrow {SA} ,\overrightarrow {AC} } \right) = {45^ \circ }\).d) \(\overrightarrow {SA} .\overrightarrow {AC} = - {a^2}\).

Phương pháp giải - Xem chi tiết Giải bài 8 trang 61 sách bài tập toán 12 - Cánh diều 1

‒ Sử dụng định lí Pitago.

‒ Sử dụng tích vô hướng của hai vectơ: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).

Lời giải chi tiết

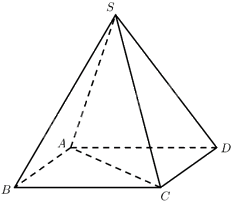
Giải bài 8 trang 61 sách bài tập toán 12 - Cánh diều 2

\(S.ABCD\) là chóp tứ giác đều nên tứ giác \(ABCD\) là hình vuông. Vậy a) đúng.

\(ABCD\) là hình vuông nên \(AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \).

Tam giác \(SAC\) có: \(S{A^2} + S{C^2} = 2{{\rm{a}}^2} = A{C^2}\).

Vậy tam giác \(SAC\) vuông cân tại \(S\). Vậy b) đúng.

\(\begin{array}{l}\cos \left( {\overrightarrow {SA} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {SA} .\overrightarrow {AC} }}{{\left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {AC} } \right|}} = \frac{{ - \overrightarrow {AS} .\overrightarrow {AC} }}{{\left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {AC} } \right|}} = \frac{{ - \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AS} ,\overrightarrow {AC} } \right)}}{{\left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {AC} } \right|}}\\ & = \frac{{ - a.a\sqrt 2 .\cos \widehat {SAC}}}{{a.a\sqrt 2 }} = \frac{{ - a.a\sqrt 2 .\cos {{45}^ \circ }}}{{a.a\sqrt 2 }} = - \frac{{\sqrt 2 }}{2}\end{array}\)

\( \Rightarrow \left( {\overrightarrow {SA} ,\overrightarrow {AC} } \right) = {135^ \circ }\). Vậy c) sai.

\(\overrightarrow{SA}.\overrightarrow{AC}=-\overrightarrow{AS}.\overrightarrow{AC}=-\left| \overrightarrow{AS} \right|.\left| \overrightarrow{AC} \right|.\cos \left( \overrightarrow{AS},\overrightarrow{AC} \right)=-a.a\sqrt{2}.\cos \widehat{SAC}=-a.a\sqrt{2}.\cos {{45}^{\circ }}=-{{a}^{2}}\)

Vậy d) đúng.

a) Đ

b) Đ

c) S

d) Đ

Giải bài 8 trang 61 SBT Toán 12 Cánh Diều: Tổng quan và Phương pháp giải

Bài 8 trang 61 sách bài tập Toán 12 Cánh Diều thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm. Bài tập này thường tập trung vào việc tìm đạo hàm của hàm số, xét tính đơn điệu của hàm số, và tìm cực trị của hàm số. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:

Định nghĩa đạo hàm: Hiểu rõ đạo hàm của một hàm số tại một điểm là gì và cách tính đạo hàm bằng định nghĩa.
Các quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của tổng, hiệu, tích, thương, và hàm hợp.
Đạo hàm của các hàm số cơ bản: Biết đạo hàm của các hàm số thường gặp như hàm số đa thức, hàm số lượng giác, hàm số mũ, hàm số logarit.
Ứng dụng của đạo hàm: Hiểu cách sử dụng đạo hàm để xét tính đơn điệu của hàm số và tìm cực trị.

Giải chi tiết bài 8 trang 61 SBT Toán 12 Cánh Diều

Để giúp các em học sinh hiểu rõ hơn về cách giải bài 8 trang 61 SBT Toán 12 Cánh Diều, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi trong bài tập. (Lưu ý: Nội dung giải chi tiết sẽ được trình bày cụ thể cho từng câu hỏi, ví dụ dưới đây chỉ mang tính minh họa)

Ví dụ: Giải câu a) bài 8 trang 61 SBT Toán 12 Cánh Diều

Đề bài: Tìm đạo hàm của hàm số f(x) = x³ - 2x² + 5x - 1.

Lời giải:

Sử dụng quy tắc đạo hàm của tổng và hiệu: f'(x) = (x³)' - (2x²)' + (5x)' - (1)'
Sử dụng quy tắc đạo hàm của lũy thừa: f'(x) = 3x² - 4x + 5 - 0
Vậy, f'(x) = 3x² - 4x + 5

Mẹo giải nhanh và hiệu quả

Để giải nhanh và hiệu quả các bài tập về đạo hàm, học sinh nên:

Luyện tập thường xuyên để nắm vững các quy tắc tính đạo hàm.
Sử dụng máy tính cầm tay để kiểm tra lại kết quả.
Phân tích kỹ đề bài để xác định đúng các hàm số cần tính đạo hàm.
Áp dụng các công thức đạo hàm một cách linh hoạt.

Tài liệu tham khảo thêm

Ngoài sách bài tập Toán 12 Cánh Diều, học sinh có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức về đạo hàm:

Sách giáo khoa Toán 12
Các bài giảng trực tuyến về đạo hàm
Các đề thi thử Toán 12

Kết luận

Hy vọng rằng lời giải chi tiết bài 8 trang 61 SBT Toán 12 Cánh Diều trên đây sẽ giúp các em học sinh hiểu rõ hơn về kiến thức và kỹ năng giải toán. Chúc các em học tập tốt!

Chủ đề	Nội dung
Đạo hàm	Định nghĩa, quy tắc tính đạo hàm
Ứng dụng đạo hàm	Xét tính đơn điệu, tìm cực trị

Giải bài 8 trang 61 sách bài tập toán 12 - Cánh diều

Giải bài 8 trang 61 SBT Toán 12 Cánh Diều

Giải bài 8 trang 61 SBT Toán 12 Cánh Diều: Tổng quan và Phương pháp giải

Giải chi tiết bài 8 trang 61 SBT Toán 12 Cánh Diều

Ví dụ: Giải câu a) bài 8 trang 61 SBT Toán 12 Cánh Diều

Mẹo giải nhanh và hiệu quả

Tài liệu tham khảo thêm

Kết luận

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN