Lý thuyết Ứng dụng hình học của tích phân Toán 12 Kết nối tri thức
Chương trình Toán 12 Kết nối tri thức, phần Ứng dụng hình học của tích phân đóng vai trò quan trọng trong việc củng cố kiến thức và rèn luyện kỹ năng giải toán. Phần này tập trung vào việc sử dụng tích phân để tính diện tích hình phẳng và thể tích vật thể tròn xoay.
Tusach.vn cung cấp tài liệu học tập đầy đủ, chi tiết, giúp học sinh dễ dàng nắm bắt kiến thức và áp dụng vào giải bài tập.
1.Ứng dụng tích phân để tính diện tích hình phẳng
a) Hình phẳng giới hạn bởi một đồ thị hàm số, trục hoành và hai đường thẳng x = a, x = b
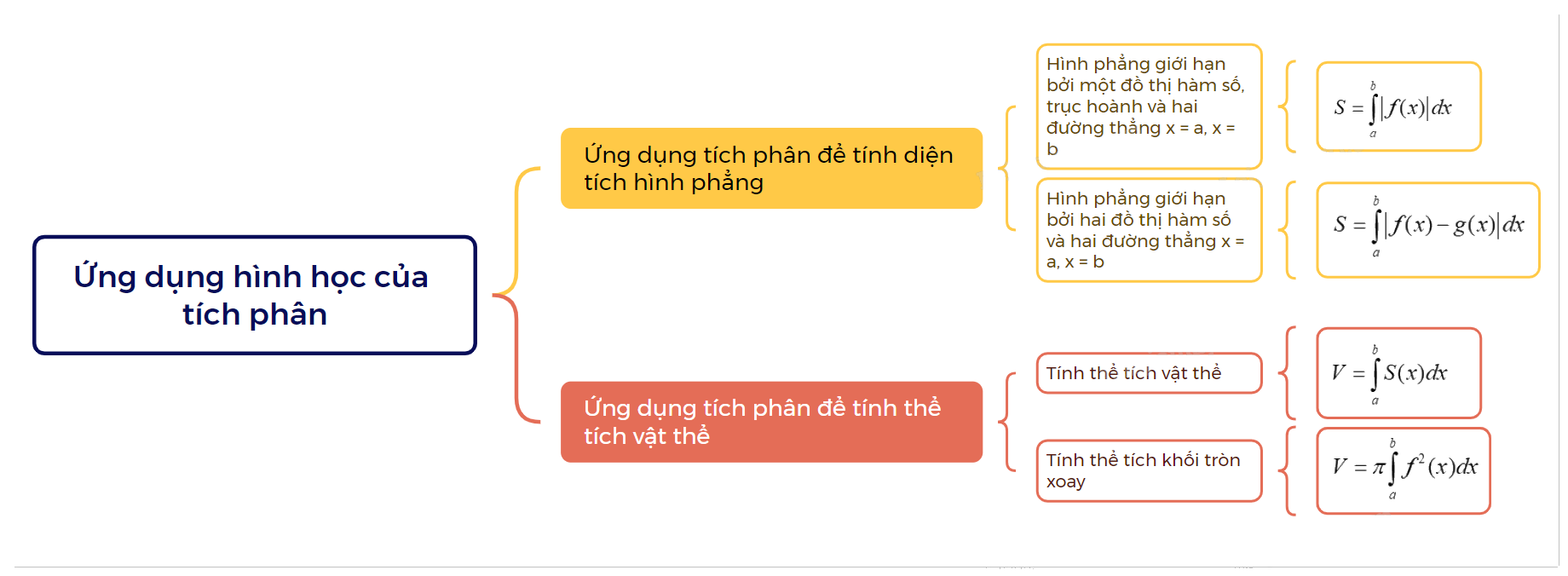
Ứng Dụng Hình Học Của Tích Phân Toán 12 Kết Nối Tri Thức: Tổng Quan Chi Tiết
Ứng dụng hình học của tích phân là một trong những nội dung quan trọng của chương trình Toán 12 Kết nối tri thức. Nó không chỉ giúp học sinh hiểu sâu hơn về tích phân mà còn cung cấp công cụ mạnh mẽ để giải quyết các bài toán thực tế liên quan đến diện tích và thể tích.
1. Tính Diện Tích Hình Phẳng
Một trong những ứng dụng quan trọng nhất của tích phân là tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục hoành (hoặc trục tung). Để tính diện tích, ta chia hình phẳng thành các hình nhỏ, tính diện tích của từng hình nhỏ, sau đó lấy tổng của các diện tích này. Trong trường hợp hình phẳng phức tạp, ta sử dụng tích phân xác định để tính diện tích một cách chính xác.
- Công thức tổng quát: Diện tích S = ∫ab |f(x)| dx, trong đó f(x) là hàm số giới hạn hình phẳng, a và b là giới hạn tích phân.
- Lưu ý: Dấu giá trị tuyệt đối đảm bảo diện tích luôn dương.
2. Tính Thể Tích Vật Thể Tròn Xoay
Tích phân cũng được sử dụng để tính thể tích của các vật thể tròn xoay, tức là các vật thể được tạo ra khi quay một đường cong hoặc một miền phẳng quanh một trục.
Có hai phương pháp chính để tính thể tích vật thể tròn xoay:
- Phương pháp đĩa: Chia vật thể tròn xoay thành các đĩa nhỏ, tính thể tích của từng đĩa, sau đó lấy tổng của các thể tích này.
- Phương pháp vỏ: Chia vật thể tròn xoay thành các vỏ nhỏ, tính thể tích của từng vỏ, sau đó lấy tổng của các thể tích này.
3. Các Ví Dụ Minh Họa
Ví dụ 1: Tính diện tích hình phẳng giới hạn bởi đường cong y = x2 và trục hoành trên đoạn [-1; 2].
Giải:
Diện tích S = ∫-12 x2 dx = [x3/3]-12 = (8/3) - (-1/3) = 3
Ví dụ 2: Tính thể tích vật thể tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đường cong y = √x, trục hoành và đường thẳng x = 4 quanh trục Ox.
Giải:
Sử dụng phương pháp đĩa: V = π∫04 (√x)2 dx = π∫04 x dx = π[x2/2]04 = 8π
4. Mẹo Giải Bài Tập
- Xác định chính xác miền tích phân: Đây là bước quan trọng nhất để đảm bảo kết quả chính xác.
- Chọn phương pháp tích phân phù hợp: Tùy thuộc vào hình dạng của miền tích phân, ta có thể chọn phương pháp đĩa hoặc phương pháp vỏ.
- Kiểm tra kết quả: Luôn kiểm tra lại kết quả bằng cách ước lượng hoặc sử dụng các công cụ tính toán.
5. Tài Liệu Tham Khảo Hữu Ích
Để học tập hiệu quả hơn, bạn có thể tham khảo các tài liệu sau:
- Sách giáo khoa Toán 12 Kết nối tri thức
- Sách bài tập Toán 12 Kết nối tri thức
- Các trang web học toán trực tuyến uy tín như tusach.vn
Hy vọng với những kiến thức và hướng dẫn trên, bạn sẽ nắm vững lý thuyết và kỹ năng giải bài tập về ứng dụng hình học của tích phân Toán 12 Kết nối tri thức. Chúc bạn học tập tốt!
