Giải mục 3 trang 28, 29, 30 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 3 trang 28, 29, 30 SGK Toán 12 tập 1 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 28, 29, 30 SGK Toán 12 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu sắc kiến thức và tự tin làm bài tập.
Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Khảo sát và vẽ đồ thị hàm số phân thức hữu tỉ
LT2
Trả lời câu hỏi Luyện tập 2 trang 29 SGK Toán 12 Kết nối tri thức
Giải bài toán ở tình huống mở đầu, coi f(x) là hàm số xác định với \(x \ge 1\).
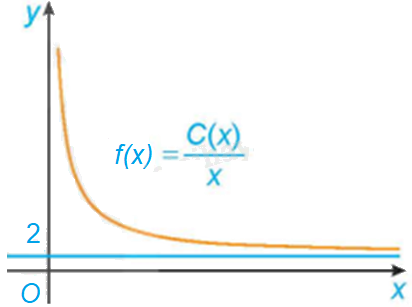
Một đơn vị sản xuất hàng tiêu dùng ước tính chi phí để sản xuất x đơn vị sản phẩm là \(C\left( x \right) = 2x + 45\) (triệu đồng). Khi đó, chi phí trung bình cho mỗi đơn vị sản phẩm là \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\). Hãy giải thích tại sao chi phí trung bình giảm theo x nhưng luôn lớn hơn 2 triệu đồng/ sản phẩm. Điều này thể hiện trên đồ thị của hàm số f(x) trong Hình 1.27 như thế nào?
Phương pháp giải:
Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\)
Lời giải chi tiết:
Ta có: \(f\left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{2x + 45}}{x}\)
Vì \(f'\left( x \right) = \frac{{ - 45}}{{{x^2}}} < 0\) với mọi \(x \ge 1\) nên hàm số \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\) là hàm số giảm.
\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 45}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 + \frac{{45}}{x}}}{1} = 2\)
Do đó, chi phí trung bình giảm theo x nhưng luôn lớn 2 triệu đồng/ sản phẩm.
Điều này được thể hiện trong Hình 1.27 là đồ thị hàm số \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\) có tiệm cận ngang là đường thẳng \(y = 2\) và đi xuống trong khoảng \(\left( {0; + \infty } \right)\).
VD
Trả lời câu hỏi Vận dụng trang 29 SGK Toán 12 Kết nối tri thức
Một bể chứa ban đầu có 200 lít nước. Sau đó, cứ mỗi phút người ta bơm thêm 40 lít nước, đồng thời cho vào bể 20 gam chất khử trùng (hòa tan).
a) Tính thể tích nước và khối lượng chất khử trùng có trong bể sau t phút. Từ đó tính nồng độ chất khử trùng (gam/lít) trong bể sau t phút.
b) Coi nồng độ chất khử trùng là hàm số f(t) với \(t \ge 0\). Khảo sát sự biến thiên và vẽ đồ thị của hàm số này.
c) Hãy giải thích tại sao nồng độ chất khử tăng theo t nhưng không vượt ngưỡng 0,5 gam/lít.
Phương pháp giải:
Sử dụng kiến thức về sơ đồ khảo sát hàm số phân thức để khảo sát và vẽ đồ thị hàm số:
Sơ đồ khảo sát hàm số phân thức
1. Tìm tập xác định của hàm số.
2. Khảo sát sự biến thiên của hàm số:
+ Tính đạo hàm y’. Tìm các điểm tại đó y’ bằng 0 hoặc đạo hàm không tồn tại.
+ Xét dấu y’ để chỉ ra các khoảng đơn điệu của hàm số.
+ Tìm cực trị của hàm số.
+ Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận của đồ thị hàm số.
+ Lập bảng biến thiên của hàm số.
3. Vẽ đồ thị của hàm số dựa vào bảng biến thiên.
Lời giải chi tiết:
a) Thể tích nước trong bể sau t phút là: \(200 + 40t\) (l).
Khối lượng chất khử trùng trong bể sau t phút là: \(20t\) (g).
Nồng độ chất khử trùng trong bể sau t phút là: \(\frac{{20t}}{{40t + 200}}\)(gam/lít).
b) Hàm số về nồng độ chất khử trùng là: \(f\left( t \right) = \frac{{20t}}{{40t + 200}},t \ge 0\)
Khảo sát và vẽ đồ thị hàm số \(y = f\left( t \right) = \frac{{20t}}{{40t + 200}},t \ge 0\).
1. Tập xác định của hàm số: \(\left[ {0; + \infty } \right)\)
2. Sự biến thiên:
Ta có: \(f'\left( t \right) = \frac{{4000}}{{{{\left( {40t + 200} \right)}^2}}} > 0\) với mọi \(t \ge 0\).
Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\).
Hàm số không có cực trị.
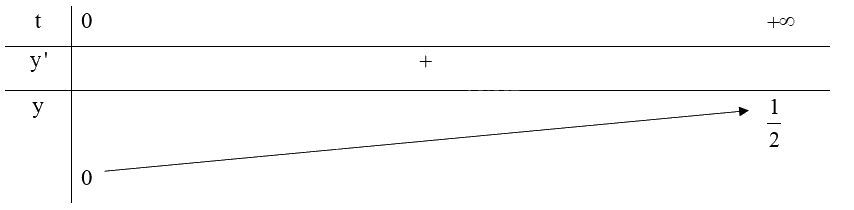
Tiệm cận: \(\mathop {\lim }\limits_{t \to + \infty } f\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } \frac{{20t}}{{40t + 200}} = \frac{1}{2}\)
Do đó, đồ thị hàm số nhận đường thẳng \(y = \frac{1}{2}\) làm tiệm cận ngang (phần bên phải trục Oy).
Bảng biến thiên:

3. Đồ thị:
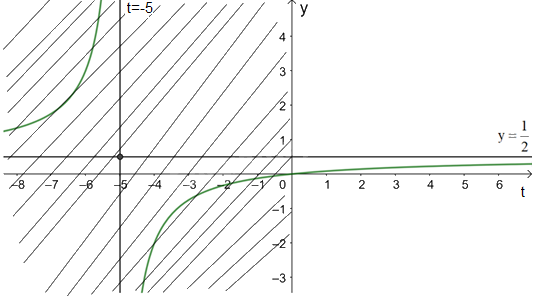
Giao điểm của đồ thị hàm số \(y = f\left( t \right) = \frac{{20t}}{{40t + 200}}\) với trục tung là \(\left( {0;0} \right)\).
Giao điểm của đồ thị hàm số với trục hoành là điểm (0; 0).
Đồ thị hàm số \(f\left( t \right) = \frac{{20t}}{{40t + 200}},t \ge 0\) là phần màu xanh không bị gạch chéo.
c) Vì \(f'\left( t \right) = \frac{{4000}}{{{{\left( {40t + 200} \right)}^2}}} > 0\) với mọi \(t \ge 0\) và \(\mathop {\lim }\limits_{t \to + \infty } f\left( t \right) = \frac{1}{2}\) nên nồng độ chất khử trùng tăng theo t nhưng không vượt ngưỡng 0,5 gam/ lít.
LT3
Trả lời câu hỏi Luyện tập 3 trang 32 SGK Toán 12 Kết nối tri thức
Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{ - {x^2} + 3x - 1}}{{x - 2}}\).
Phương pháp giải:
Sử dụng kiến thức về sơ đồ khảo sát hàm số phân thức để khảo sát và vẽ đồ thị hàm số:
Sơ đồ khảo sát hàm số phân thức
1. Tìm tập xác định của hàm số.
2. Khảo sát sự biến thiên của hàm số:
+ Tính đạo hàm y’. Tìm các điểm tại đó y’ bằng 0 hoặc đạo hàm không tồn tại.
+ Xét dấu y’ để chỉ ra các khoảng đơn điệu của hàm số.
+ Tìm cực trị của hàm số.
+ Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận của đồ thị hàm số.
+ Lập bảng biến thiên của hàm số.
3. Vẽ đồ thị của hàm số dựa vào bảng biến thiên.
Lời giải chi tiết:
1. Tập xác định của hàm số: \(\mathbb{R}\backslash \left\{ 2 \right\}\)
2. Sự biến thiên:
Ta có: \(y = \frac{{ - {x^2} + 3x - 1}}{{x - 2}} = - x + 1 + \frac{1}{{x - 2}}\)
\(y' = - 1 - \frac{1}{{{{\left( {x - 2} \right)}^2}}} < 0\forall x \ne 2\)
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).
Hàm số không có cực trị.
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - {x^2} + 3x - 1}}{{x - 2}} = - \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - {x^2} + 3x - 1}}{{x - 2}} = + \infty \) \(\mathop {\lim }\limits_{x \to {2^ - }} y = \mathop {\lim }\limits_{x \to {2^ - }} \frac{{ - {x^2} + 3x - 1}}{{x - 2}} = - \infty ;\mathop {\lim }\limits_{x \to {2^ + }} y = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{ - {x^2} + 3x - 1}}{{x - 2}} = + \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( { - x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left( { - x + 1 + \frac{1}{{x - 2}} + x - 1} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x - 2}} = 0\)
\(\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( { - x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \left( { - x + 1 + \frac{1}{{x - 2}} + x - 1} \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x - 2}} = 0\)
Do đó, đồ thị hàm số nhận đường thẳng \(x = 2\) làm tiệm cận đứng và đường thẳng \(y = - x + 1\) làm tiệm cận xiên.
Bảng biến thiên:

3. Đồ thị:
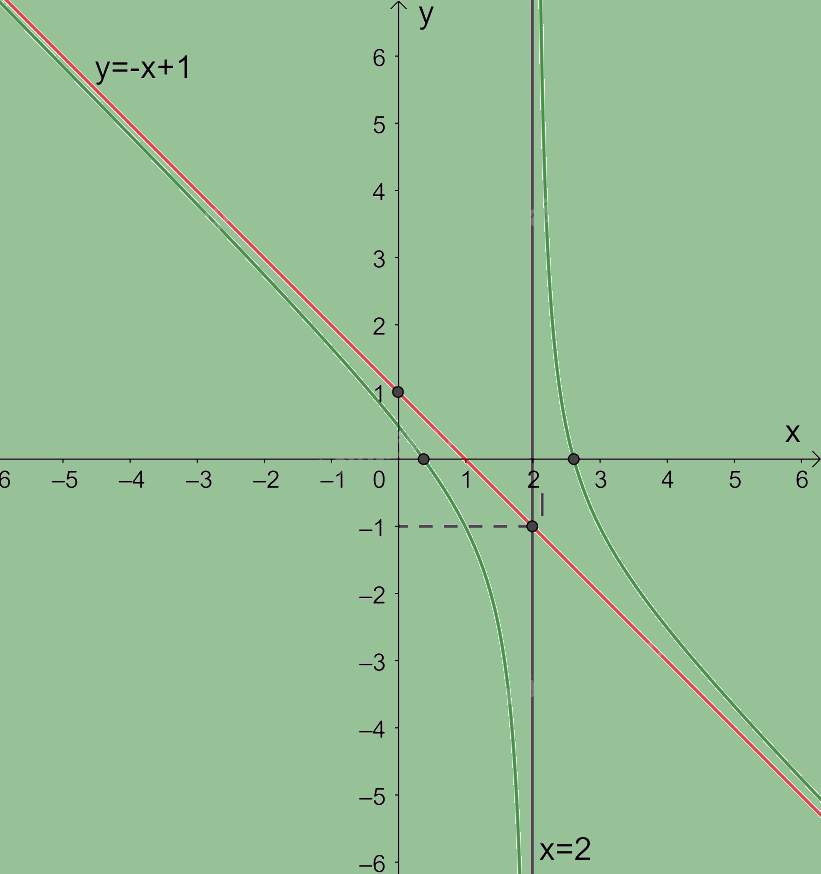
Giao điểm của đồ thị hàm số với trục tung là \(\left( {0;\frac{1}{2}} \right)\).
\(y = 0 \Leftrightarrow \frac{{ - {x^2} + 3x - 1}}{{x - 2}} = 0 \Leftrightarrow x = \frac{{3 + \sqrt 5 }}{2}\) hoặc \(x = \frac{{3 - \sqrt 5 }}{2}\)
Giao điểm của đồ thị hàm số với trục hoành là các điểm\(\left( {\frac{{3 + \sqrt 5 }}{2};0} \right);\left( {\frac{{3 - \sqrt 5 }}{2};0} \right)\).
Đồ thị hàm số nhận giao điểm \(I\left( {2; - 1} \right)\) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
- LT2
- VD
- LT3
Trả lời câu hỏi Luyện tập 2 trang 29 SGK Toán 12 Kết nối tri thức
Giải bài toán ở tình huống mở đầu, coi f(x) là hàm số xác định với \(x \ge 1\).
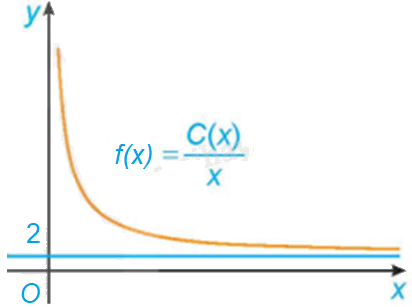
Một đơn vị sản xuất hàng tiêu dùng ước tính chi phí để sản xuất x đơn vị sản phẩm là \(C\left( x \right) = 2x + 45\) (triệu đồng). Khi đó, chi phí trung bình cho mỗi đơn vị sản phẩm là \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\). Hãy giải thích tại sao chi phí trung bình giảm theo x nhưng luôn lớn hơn 2 triệu đồng/ sản phẩm. Điều này thể hiện trên đồ thị của hàm số f(x) trong Hình 1.27 như thế nào?
Phương pháp giải:
Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\)
Lời giải chi tiết:
Ta có: \(f\left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{2x + 45}}{x}\)
Vì \(f'\left( x \right) = \frac{{ - 45}}{{{x^2}}} < 0\) với mọi \(x \ge 1\) nên hàm số \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\) là hàm số giảm.
\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 45}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 + \frac{{45}}{x}}}{1} = 2\)
Do đó, chi phí trung bình giảm theo x nhưng luôn lớn 2 triệu đồng/ sản phẩm.
Điều này được thể hiện trong Hình 1.27 là đồ thị hàm số \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\) có tiệm cận ngang là đường thẳng \(y = 2\) và đi xuống trong khoảng \(\left( {0; + \infty } \right)\).
Trả lời câu hỏi Vận dụng trang 29 SGK Toán 12 Kết nối tri thức
Một bể chứa ban đầu có 200 lít nước. Sau đó, cứ mỗi phút người ta bơm thêm 40 lít nước, đồng thời cho vào bể 20 gam chất khử trùng (hòa tan).
a) Tính thể tích nước và khối lượng chất khử trùng có trong bể sau t phút. Từ đó tính nồng độ chất khử trùng (gam/lít) trong bể sau t phút.
b) Coi nồng độ chất khử trùng là hàm số f(t) với \(t \ge 0\). Khảo sát sự biến thiên và vẽ đồ thị của hàm số này.
c) Hãy giải thích tại sao nồng độ chất khử tăng theo t nhưng không vượt ngưỡng 0,5 gam/lít.
Phương pháp giải:
Sử dụng kiến thức về sơ đồ khảo sát hàm số phân thức để khảo sát và vẽ đồ thị hàm số:
Sơ đồ khảo sát hàm số phân thức
1. Tìm tập xác định của hàm số.
2. Khảo sát sự biến thiên của hàm số:
+ Tính đạo hàm y’. Tìm các điểm tại đó y’ bằng 0 hoặc đạo hàm không tồn tại.
+ Xét dấu y’ để chỉ ra các khoảng đơn điệu của hàm số.
+ Tìm cực trị của hàm số.
+ Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận của đồ thị hàm số.
+ Lập bảng biến thiên của hàm số.
3. Vẽ đồ thị của hàm số dựa vào bảng biến thiên.
Lời giải chi tiết:
a) Thể tích nước trong bể sau t phút là: \(200 + 40t\) (l).
Khối lượng chất khử trùng trong bể sau t phút là: \(20t\) (g).
Nồng độ chất khử trùng trong bể sau t phút là: \(\frac{{20t}}{{40t + 200}}\)(gam/lít).
b) Hàm số về nồng độ chất khử trùng là: \(f\left( t \right) = \frac{{20t}}{{40t + 200}},t \ge 0\)
Khảo sát và vẽ đồ thị hàm số \(y = f\left( t \right) = \frac{{20t}}{{40t + 200}},t \ge 0\).
1. Tập xác định của hàm số: \(\left[ {0; + \infty } \right)\)
2. Sự biến thiên:
Ta có: \(f'\left( t \right) = \frac{{4000}}{{{{\left( {40t + 200} \right)}^2}}} > 0\) với mọi \(t \ge 0\).
Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\).
Hàm số không có cực trị.
Tiệm cận: \(\mathop {\lim }\limits_{t \to + \infty } f\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } \frac{{20t}}{{40t + 200}} = \frac{1}{2}\)
Do đó, đồ thị hàm số nhận đường thẳng \(y = \frac{1}{2}\) làm tiệm cận ngang (phần bên phải trục Oy).
Bảng biến thiên:
3. Đồ thị:
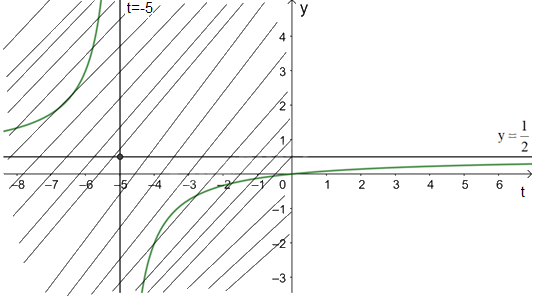
Giao điểm của đồ thị hàm số \(y = f\left( t \right) = \frac{{20t}}{{40t + 200}}\) với trục tung là \(\left( {0;0} \right)\).
Giao điểm của đồ thị hàm số với trục hoành là điểm (0; 0).
Đồ thị hàm số \(f\left( t \right) = \frac{{20t}}{{40t + 200}},t \ge 0\) là phần màu xanh không bị gạch chéo.
c) Vì \(f'\left( t \right) = \frac{{4000}}{{{{\left( {40t + 200} \right)}^2}}} > 0\) với mọi \(t \ge 0\) và \(\mathop {\lim }\limits_{t \to + \infty } f\left( t \right) = \frac{1}{2}\) nên nồng độ chất khử trùng tăng theo t nhưng không vượt ngưỡng 0,5 gam/ lít.
Trả lời câu hỏi Luyện tập 3 trang 32 SGK Toán 12 Kết nối tri thức
Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{ - {x^2} + 3x - 1}}{{x - 2}}\).
Phương pháp giải:
Sử dụng kiến thức về sơ đồ khảo sát hàm số phân thức để khảo sát và vẽ đồ thị hàm số:
Sơ đồ khảo sát hàm số phân thức
1. Tìm tập xác định của hàm số.
2. Khảo sát sự biến thiên của hàm số:
+ Tính đạo hàm y’. Tìm các điểm tại đó y’ bằng 0 hoặc đạo hàm không tồn tại.
+ Xét dấu y’ để chỉ ra các khoảng đơn điệu của hàm số.
+ Tìm cực trị của hàm số.
+ Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận của đồ thị hàm số.
+ Lập bảng biến thiên của hàm số.
3. Vẽ đồ thị của hàm số dựa vào bảng biến thiên.
Lời giải chi tiết:
1. Tập xác định của hàm số: \(\mathbb{R}\backslash \left\{ 2 \right\}\)
2. Sự biến thiên:
Ta có: \(y = \frac{{ - {x^2} + 3x - 1}}{{x - 2}} = - x + 1 + \frac{1}{{x - 2}}\)
\(y' = - 1 - \frac{1}{{{{\left( {x - 2} \right)}^2}}} < 0\forall x \ne 2\)
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).
Hàm số không có cực trị.
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - {x^2} + 3x - 1}}{{x - 2}} = - \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - {x^2} + 3x - 1}}{{x - 2}} = + \infty \) \(\mathop {\lim }\limits_{x \to {2^ - }} y = \mathop {\lim }\limits_{x \to {2^ - }} \frac{{ - {x^2} + 3x - 1}}{{x - 2}} = - \infty ;\mathop {\lim }\limits_{x \to {2^ + }} y = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{ - {x^2} + 3x - 1}}{{x - 2}} = + \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( { - x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left( { - x + 1 + \frac{1}{{x - 2}} + x - 1} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x - 2}} = 0\)
\(\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( { - x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \left( { - x + 1 + \frac{1}{{x - 2}} + x - 1} \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x - 2}} = 0\)
Do đó, đồ thị hàm số nhận đường thẳng \(x = 2\) làm tiệm cận đứng và đường thẳng \(y = - x + 1\) làm tiệm cận xiên.
Bảng biến thiên:

3. Đồ thị:
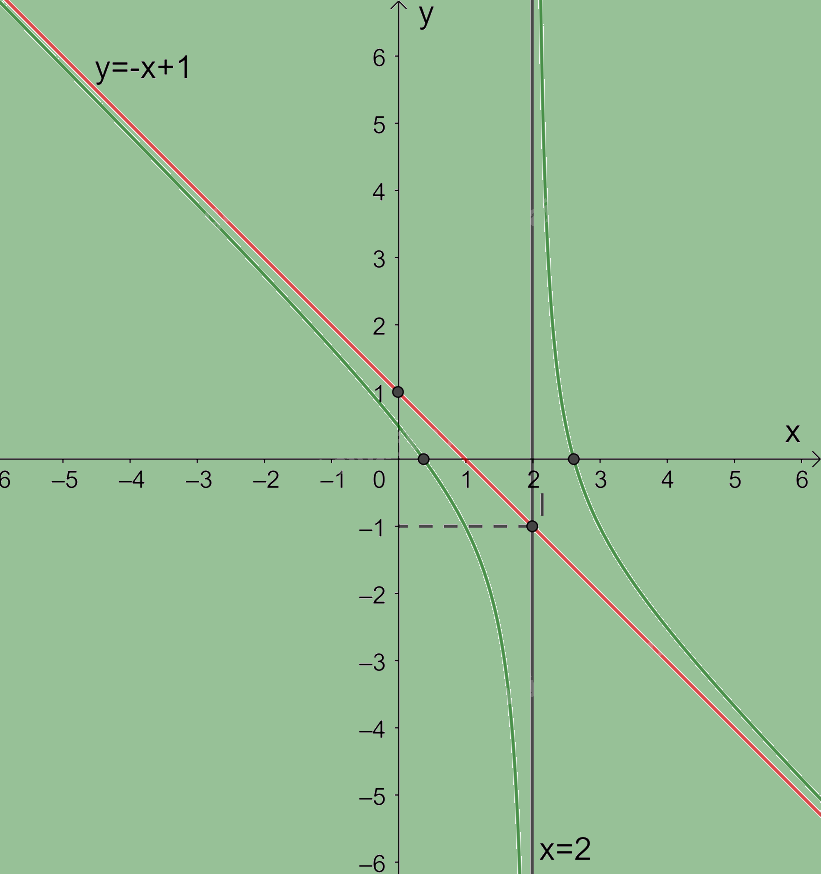
Giao điểm của đồ thị hàm số với trục tung là \(\left( {0;\frac{1}{2}} \right)\).
\(y = 0 \Leftrightarrow \frac{{ - {x^2} + 3x - 1}}{{x - 2}} = 0 \Leftrightarrow x = \frac{{3 + \sqrt 5 }}{2}\) hoặc \(x = \frac{{3 - \sqrt 5 }}{2}\)
Giao điểm của đồ thị hàm số với trục hoành là các điểm\(\left( {\frac{{3 + \sqrt 5 }}{2};0} \right);\left( {\frac{{3 - \sqrt 5 }}{2};0} \right)\).
Đồ thị hàm số nhận giao điểm \(I\left( {2; - 1} \right)\) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
Giải mục 3 trang 28, 29, 30 SGK Toán 12 tập 1 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 3 của SGK Toán 12 tập 1 Kết nối tri thức thường xoay quanh các chủ đề về giới hạn của hàm số. Đây là một phần kiến thức nền tảng quan trọng, không chỉ cho việc học tập ở bậc THPT mà còn là bước đệm cho các kiến thức nâng cao ở bậc đại học.
Nội dung chính của Mục 3
- Khái niệm giới hạn của hàm số tại một điểm: Hiểu rõ định nghĩa, ý nghĩa của giới hạn.
- Các tính chất của giới hạn: Nắm vững các tính chất cơ bản để đơn giản hóa việc tính toán giới hạn.
- Các dạng giới hạn thường gặp: Làm quen với các dạng giới hạn quen thuộc và phương pháp giải tương ứng.
- Ứng dụng của giới hạn: Giải các bài toán liên quan đến sự liên tục của hàm số.
Giải chi tiết bài tập trang 28, 29, 30
Bài 1: Tính các giới hạn sau (trang 28)
a) lim (x→2) (x^2 - 4) / (x - 2)
Lời giải: Ta có thể phân tích tử thức thành (x - 2)(x + 2). Khi đó:
lim (x→2) (x^2 - 4) / (x - 2) = lim (x→2) (x - 2)(x + 2) / (x - 2) = lim (x→2) (x + 2) = 4
b) lim (x→-1) (x^3 + 1) / (x + 1)
Lời giải: Tương tự, ta phân tích tử thức thành (x + 1)(x^2 - x + 1). Khi đó:
lim (x→-1) (x^3 + 1) / (x + 1) = lim (x→-1) (x + 1)(x^2 - x + 1) / (x + 1) = lim (x→-1) (x^2 - x + 1) = 3
Bài 2: Tính các giới hạn sau (trang 29)
a) lim (x→∞) (2x + 1) / (x - 3)
Lời giải: Chia cả tử và mẫu cho x, ta được:
lim (x→∞) (2x + 1) / (x - 3) = lim (x→∞) (2 + 1/x) / (1 - 3/x) = 2/1 = 2
Bài 3: (trang 30)
Bài 3 thường là bài toán ứng dụng, yêu cầu học sinh vận dụng kiến thức về giới hạn để chứng minh sự liên tục của hàm số hoặc giải các bài toán thực tế. (Nội dung cụ thể của bài 3 sẽ được giải chi tiết tùy thuộc vào đề bài)
Mẹo giải bài tập về giới hạn
- Phân tích tử và mẫu: Tìm các nhân tử chung để rút gọn biểu thức.
- Chia cả tử và mẫu cho x: Khi tính giới hạn tại vô cùng.
- Sử dụng các tính chất của giới hạn: Để đơn giản hóa biểu thức.
- Áp dụng các công thức giới hạn đặc biệt: Ví dụ: lim (x→0) sin(x)/x = 1
Tusach.vn - Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn tự hào là một trong những website cung cấp tài liệu học tập Toán 12 uy tín và chất lượng nhất. Chúng tôi luôn cập nhật lời giải chi tiết, chính xác và dễ hiểu cho tất cả các bài tập trong SGK và SBT Toán 12. Hãy truy cập tusach.vn để đồng hành cùng chúng tôi trên con đường chinh phục môn Toán!