Giải mục 1 trang 50,51 SGK Toán 12 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải mục 1 trang 50,51 SGK Toán 12 tập 2 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 50, 51 sách giáo khoa Toán 12 tập 2 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em học sinh hiểu rõ các khái niệm, định lý và phương pháp giải bài tập liên quan.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, đầy đủ và cập nhật nhất để hỗ trợ các em trong quá trình học tập.
CÔNG THỨC TÍNH GÓC GIỮA HAI ĐƯỜNG THẲNG
LT1
Trả lời câu hỏi Luyện tập 1 trang 51 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, tính góc giữa trục Oz và đường thẳng \(\Delta :\frac{{x - 3}}{1} = \frac{{y + 1}}{2} = \frac{{z - 1}}{{ - 2}}\).
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai đường thẳng để tính: Trong không gian Oxyz, cho hai đường thẳng \(\Delta \) và \(\Delta '\) tương ứng có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right),\overrightarrow {u'} = \left( {a';b';c'} \right)\). Khi đó: \(\cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right| = \frac{{\left| {aa' + bb' + cc'} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} .\sqrt {a{'^2} + b{'^2} + c{'^2}} }}\).
Lời giải chi tiết:
Trục Oz có vectơ chỉ phương \(\overrightarrow k = \left( {0;0;1} \right)\), đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow u \left( {1;2; - 2} \right)\). Do đó, \(\cos \left( {Oz,\Delta } \right) = \left| {\cos \left( {\overrightarrow k ,\overrightarrow u } \right)} \right| = \frac{{\left| {0.1 + 0.2 - 1.2} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} .\sqrt {{1^2} + {2^2} + {{\left( { - 2} \right)}^2}} }} = \frac{2}{3}\)
Suy ra: \(\left( {Oz,\Delta } \right) \approx 48,{2^o}\).
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 50 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai đường thẳng \(\Delta \) và \(\Delta '\) tương ứng có các vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right),\overrightarrow {u'} = \left( {a';b';c'} \right)\). (H.5.34).
a) Hãy tìm mối quan hệ giữa các góc \(\left( {\Delta ,\Delta '} \right)\) và \(\left( {\overrightarrow u ,\overrightarrow {u'} } \right)\).
b) Có nhận xét gì về mối quan hệ giữa \(\cos \left( {\Delta ,\Delta '} \right)\) và \(\left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right|\)?
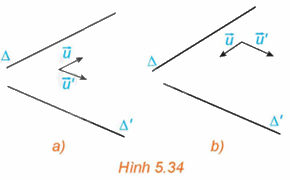
Phương pháp giải:
Sử dụng kiến thức giá của vectơ để chứng minh: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ đó.
Lời giải chi tiết:
a) Vì \(\overrightarrow u \) và \(\overrightarrow {u'} \) lần lượt là các vectơ chỉ phương của hai đường thẳng \(\Delta \) và \(\Delta '\). Do đó, giá của \(\overrightarrow u \) song song với \(\Delta \), giá của \(\overrightarrow {u'} \) song song với \(\Delta '\). Do đó:
+) \(\left( {\Delta ,\Delta '} \right) = \left( {\overrightarrow u ,\overrightarrow {u'} } \right)\) nếu \(\left( {\overrightarrow u ,\overrightarrow {u'} } \right) \le {90^o}\)
+) \(\left( {\Delta ,\Delta '} \right) = {180^o} - \left( {\overrightarrow u ,\overrightarrow {u'} } \right)\) nếu \(\left( {\overrightarrow u ,\overrightarrow {u'} } \right) > {90^o}\)
b) Ta có: \(\cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right|\).
- HĐ1
- LT1
Trả lời câu hỏi Hoạt động 1 trang 50 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai đường thẳng \(\Delta \) và \(\Delta '\) tương ứng có các vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right),\overrightarrow {u'} = \left( {a';b';c'} \right)\). (H.5.34).
a) Hãy tìm mối quan hệ giữa các góc \(\left( {\Delta ,\Delta '} \right)\) và \(\left( {\overrightarrow u ,\overrightarrow {u'} } \right)\).
b) Có nhận xét gì về mối quan hệ giữa \(\cos \left( {\Delta ,\Delta '} \right)\) và \(\left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right|\)?
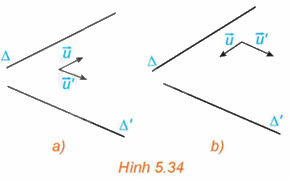
Phương pháp giải:
Sử dụng kiến thức giá của vectơ để chứng minh: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ đó.
Lời giải chi tiết:
a) Vì \(\overrightarrow u \) và \(\overrightarrow {u'} \) lần lượt là các vectơ chỉ phương của hai đường thẳng \(\Delta \) và \(\Delta '\). Do đó, giá của \(\overrightarrow u \) song song với \(\Delta \), giá của \(\overrightarrow {u'} \) song song với \(\Delta '\). Do đó:
+) \(\left( {\Delta ,\Delta '} \right) = \left( {\overrightarrow u ,\overrightarrow {u'} } \right)\) nếu \(\left( {\overrightarrow u ,\overrightarrow {u'} } \right) \le {90^o}\)
+) \(\left( {\Delta ,\Delta '} \right) = {180^o} - \left( {\overrightarrow u ,\overrightarrow {u'} } \right)\) nếu \(\left( {\overrightarrow u ,\overrightarrow {u'} } \right) > {90^o}\)
b) Ta có: \(\cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right|\).
Trả lời câu hỏi Luyện tập 1 trang 51 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, tính góc giữa trục Oz và đường thẳng \(\Delta :\frac{{x - 3}}{1} = \frac{{y + 1}}{2} = \frac{{z - 1}}{{ - 2}}\).
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai đường thẳng để tính: Trong không gian Oxyz, cho hai đường thẳng \(\Delta \) và \(\Delta '\) tương ứng có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right),\overrightarrow {u'} = \left( {a';b';c'} \right)\). Khi đó: \(\cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right| = \frac{{\left| {aa' + bb' + cc'} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} .\sqrt {a{'^2} + b{'^2} + c{'^2}} }}\).
Lời giải chi tiết:
Trục Oz có vectơ chỉ phương \(\overrightarrow k = \left( {0;0;1} \right)\), đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow u \left( {1;2; - 2} \right)\). Do đó, \(\cos \left( {Oz,\Delta } \right) = \left| {\cos \left( {\overrightarrow k ,\overrightarrow u } \right)} \right| = \frac{{\left| {0.1 + 0.2 - 1.2} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} .\sqrt {{1^2} + {2^2} + {{\left( { - 2} \right)}^2}} }} = \frac{2}{3}\)
Suy ra: \(\left( {Oz,\Delta } \right) \approx 48,{2^o}\).
Giải mục 1 trang 50,51 SGK Toán 12 tập 2 - Kết nối tri thức: Tổng quan và Phương pháp
Mục 1 trang 50, 51 SGK Toán 12 tập 2 - Kết nối tri thức tập trung vào việc ôn tập chương 3: Đạo hàm. Đây là một phần quan trọng trong chương trình Toán 12, nền tảng cho việc giải quyết các bài toán phức tạp hơn trong các chương tiếp theo và kỳ thi tốt nghiệp THPT. Việc nắm vững kiến thức về đạo hàm là điều kiện cần thiết để hiểu và vận dụng tốt các khái niệm về tích phân, hình học giải tích và các ứng dụng khác của Toán học.
Nội dung chính của Mục 1
- Ôn tập các khái niệm cơ bản về đạo hàm: Định nghĩa đạo hàm, ý nghĩa hình học và vật lý của đạo hàm, các quy tắc tính đạo hàm (đạo hàm của tổng, hiệu, tích, thương, hàm hợp).
- Các đạo hàm đặc biệt: Đạo hàm của các hàm số lượng giác, hàm số mũ, hàm số logarit.
- Ứng dụng của đạo hàm: Tìm cực trị của hàm số, khảo sát hàm số, giải phương trình, bất phương trình.
Giải chi tiết các bài tập trong Mục 1
Dưới đây là lời giải chi tiết cho các bài tập trong mục 1 trang 50, 51 SGK Toán 12 tập 2 - Kết nối tri thức:
Bài 1: Tính đạo hàm của các hàm số sau
- f(x) = x3 - 2x2 + 5x - 1
- g(x) = sin(x) + cos(x)
- h(x) = ex + ln(x)
Lời giải:
- f'(x) = 3x2 - 4x + 5
- g'(x) = cos(x) - sin(x)
- h'(x) = ex + 1/x
Bài 2: Tìm cực trị của hàm số y = x3 - 3x2 + 2
Lời giải:
y' = 3x2 - 6x
Giải phương trình y' = 0, ta được x = 0 hoặc x = 2
Tính y'' = 6x - 6
y''(0) = -6 < 0 => Hàm số đạt cực đại tại x = 0, ymax = 2
y''(2) = 6 > 0 => Hàm số đạt cực tiểu tại x = 2, ymin = -2
Bài 3: Khảo sát hàm số y = x4 - 4x2 + 3
Lời giải:
(Phần giải bài khảo sát hàm số đầy đủ, bao gồm tập xác định, giới hạn, cực trị, điểm uốn, khoảng đơn điệu, và vẽ đồ thị)
Mẹo giải nhanh và hiệu quả
Để giải các bài tập về đạo hàm một cách nhanh chóng và hiệu quả, bạn nên:
- Nắm vững các quy tắc tính đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính cầm tay để kiểm tra lại kết quả.
- Tham khảo các tài liệu tham khảo, sách bài tập và các trang web học tập trực tuyến.
Tài liệu tham khảo hữu ích
- Sách giáo khoa Toán 12 tập 2 - Kết nối tri thức
- Sách bài tập Toán 12 tập 2 - Kết nối tri thức
- Các trang web học tập trực tuyến như tusach.vn, loigiaihay.com, vted.vn
Hy vọng bài viết này sẽ giúp các em học sinh giải quyết tốt các bài tập trong mục 1 trang 50, 51 SGK Toán 12 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!