Giải bài tập 2.42 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 2.42 Trang 74 Toán 12 Tập 1 - Kết Nối Tri Thức
Bài tập 2.42 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức là một bài toán quan trọng trong chương trình học. Bài viết này của tusach.vn sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và kỹ năng giải toán.
Chúng tôi sẽ trình bày đầy đủ các bước giải, phân tích rõ ràng từng bước để các em có thể tự tin áp dụng vào các bài tập tương tự.
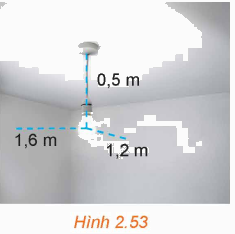
Hình 2.53 minh họa một chiếc đèn được treo cách trần nhà 0,5m, cách hai tường lần lượt là 1,2m và 1,6m. Hai bức tường vuông góc với nhau và cùng vuông góc với trần nhà. Người ta di chuyển chiếc đèn đó đến vị trí mới cách trần nhà là 0,4m, cách hai tường đều là 1,5m. a) Lập một hệ trục tọa độ Oxyz phù hợp và xác định tọa độ của bóng đèn lúc đầu và sau khi di chuyển. b) Vị trí mới của bóng đèn cách vị trí ban đầu là bao nhiêu mét? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
Đề bài
Hình 2.53 minh họa một chiếc đèn được treo cách trần nhà 0,5m, cách hai tường lần lượt là 1,2m và 1,6m. Hai bức tường vuông góc với nhau và cùng vuông góc với trần nhà. Người ta di chuyển chiếc đèn đó đến vị trí mới cách trần nhà là 0,4m, cách hai tường đều là 1,5m.a) Lập một hệ trục tọa độ Oxyz phù hợp và xác định tọa độ của bóng đèn lúc đầu và sau khi di chuyển.b) Vị trí mới của bóng đèn cách vị trí ban đầu là bao nhiêu mét? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về hệ tọa độ trong không gian để giải thích: Trong không gian, ba trục Ox, Oy, Oz đôi một vuông góc với nhau tại gốc O của mỗi trục. Gọi \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) lần lượt là các vectơ đơn vị trên các trục Ox, Oy, Oz. Hệ ba trục tọa độ như vậy được gọi là hệ trục tọa độ Descartes vuông góc Oxyz (hay đơn giản là hệ tọa độ Oxyz). Điểm O được gọi là gốc tọa độ, các mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau và được gọi là các mặt phẳng tọa độ. Không gian với hệ tọa độ Oxyz còn được gọi là không gian Oxyz.
b) Sử dụng kiến thức về độ dài đoạn thẳng trong không gian để tính: Nếu \(A\left( {{x_A};{y_A};{z_A}} \right)\) và \(B\left( {{x_B};{y_B};{z_B}} \right)\) thì \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \).
Lời giải chi tiết
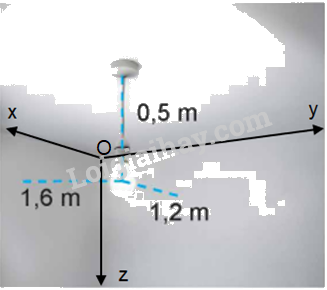
a) Chọn hệ trục tọa độ Oxyz như sau:
+ Gốc O trùng với một góc của phòng
+ Mặt phẳng (Oxy) trùng với trần nhà, mặt phẳng (Oxz) và mặt phẳng (Oyz) trùng với hai bức tường (như hình vẽ).
Tọa độ của bóng đèn lúc đầu là A(1,6; 1,2; 0,5)
Tọa độ bóng đèn sau khi di chuyển là: B(1,5; 1,5; 0,4)
Giải Bài Tập 2.42 Trang 74 SGK Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 2.42 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức thuộc chương trình học về đạo hàm. Bài toán này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết. Dưới đây là lời giải chi tiết và các lưu ý quan trọng:
Đề Bài
Cho hàm số y = f(x) có đạo hàm f'(x) = (x-1)^2(x+2). Hỏi hàm số y = f(x) đồng biến trên khoảng nào?
Lời Giải
Để hàm số y = f(x) đồng biến trên một khoảng, cần có f'(x) > 0. Ta xét dấu của f'(x) = (x-1)^2(x+2):
- (x-1)^2 ≥ 0 với mọi x
- x + 2 > 0 khi x > -2
Vậy, f'(x) > 0 khi x > -2 và x ≠ 1. Do đó, hàm số y = f(x) đồng biến trên các khoảng (-2; 1) và (1; +∞).
Phân Tích Chi Tiết
Bài toán này đòi hỏi học sinh phải hiểu rõ về điều kiện đồng biến của hàm số. Cụ thể, hàm số đồng biến khi đạo hàm của nó lớn hơn 0. Việc xét dấu đạo hàm là bước quan trọng để xác định khoảng đồng biến. Trong trường hợp này, (x-1)^2 luôn dương (hoặc bằng 0) nên ta chỉ cần xét dấu của (x+2). Lưu ý rằng tại x = 1, đạo hàm bằng 0 nên hàm số không đồng biến tại điểm này.
Các Dạng Bài Tập Tương Tự
Ngoài bài tập 2.42, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về đạo hàm để xét tính đơn điệu của hàm số. Một số dạng bài tập thường gặp:
- Xác định khoảng đồng biến, nghịch biến của hàm số.
- Tìm giá trị của tham số để hàm số đồng biến hoặc nghịch biến trên một khoảng cho trước.
- Chứng minh hàm số đồng biến hoặc nghịch biến trên một khoảng.
Mẹo Giải Bài Tập Đạo Hàm
Để giải tốt các bài tập về đạo hàm, các em học sinh nên:
- Nắm vững các công thức đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Phân tích kỹ đề bài để xác định đúng phương pháp giải.
- Kiểm tra lại kết quả sau khi giải xong.
Kết Luận
Bài tập 2.42 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập điển hình về ứng dụng của đạo hàm trong việc xét tính đơn điệu của hàm số. Hy vọng với lời giải chi tiết và các phân tích trên, các em học sinh đã hiểu rõ cách giải bài tập này và có thể tự tin áp dụng vào các bài tập tương tự. Hãy tiếp tục luyện tập để nâng cao kiến thức và kỹ năng giải toán của mình!
Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Hãy truy cập website của chúng tôi để xem thêm nhiều bài giải và tài liệu học tập hữu ích khác.
| Khái niệm | Giải thích |
|---|---|
| Đạo hàm | Tốc độ thay đổi tức thời của hàm số. |
| Hàm số đồng biến | Hàm số tăng khi x tăng. |
| Hàm số nghịch biến | Hàm số giảm khi x tăng. |
| Nguồn: tusach.vn | |