Giải Bài Tập 2.7 Trang 58 Toán 12 Tập 1 - Kết Nối Tri Thức
Bài tập 2.7 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.
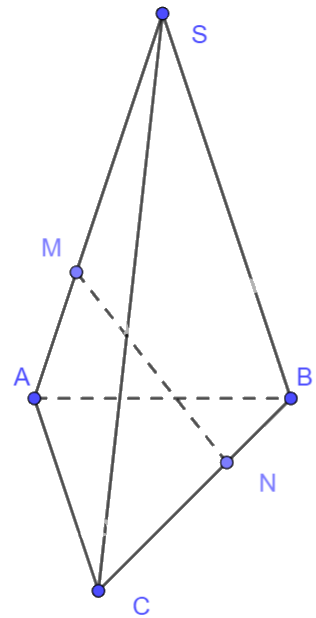
Cho hình chóp S.ABC. Trên cạnh SA, lấy điểm M sao cho \(SM = 2AM\). Trên cạnh BC, lấy điểm N sao cho \(CN = 2BN\). Chứng minh rằng \(\overrightarrow {MN} = \frac{1}{3}\left( {\overrightarrow {SA} + \overrightarrow {BC} } \right) + \overrightarrow {AB} \).
Giải Bài Tập 2.7 Trang 58 Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 2.7 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
- Định nghĩa đạo hàm của hàm số tại một điểm.
- Các quy tắc tính đạo hàm (đạo hàm của tổng, hiệu, tích, thương, hàm hợp).
- Đạo hàm của các hàm số cơ bản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit).
Nội Dung Bài Tập 2.7
Bài tập 2.7 thường yêu cầu học sinh thực hiện các thao tác sau:
- Tính đạo hàm của hàm số tại một điểm cho trước.
- Tìm đạo hàm của hàm số.
- Xác định các điểm mà tại đó hàm số không có đạo hàm.
- Vận dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến của đồ thị hàm số, vận tốc tức thời, gia tốc tức thời,...
Lời Giải Chi Tiết Bài Tập 2.7 (Ví dụ)
Để minh họa, chúng ta sẽ xét một ví dụ cụ thể. Giả sử bài tập 2.7 yêu cầu tính đạo hàm của hàm số f(x) = x2 + 2x - 1 tại điểm x = 1.
Bước 1: Áp dụng quy tắc đạo hàm của hàm đa thức:
f'(x) = 2x + 2
Bước 2: Thay x = 1 vào đạo hàm vừa tìm được:
f'(1) = 2(1) + 2 = 4
Vậy, đạo hàm của hàm số f(x) tại điểm x = 1 là 4.
Mẹo Giải Bài Tập Đạo Hàm Hiệu Quả
- Nắm vững các quy tắc tính đạo hàm: Đây là nền tảng để giải quyết mọi bài tập về đạo hàm.
- Phân tích kỹ đề bài: Xác định rõ yêu cầu của bài toán để lựa chọn phương pháp giải phù hợp.
- Thực hành thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập.
- Sử dụng các công cụ hỗ trợ: Các công cụ tính đạo hàm trực tuyến có thể giúp bạn kiểm tra lại kết quả và tiết kiệm thời gian.
Tusach.vn - Đồng Hành Cùng Bạn Học Toán 12
Tusach.vn là website học tập trực tuyến uy tín, cung cấp đầy đủ các tài liệu học tập Toán 12, bao gồm:
- Giải bài tập SGK Toán 12 tập 1 và tập 2.
- Giải bài tập trắc nghiệm Toán 12.
- Bài giảng video Toán 12.
- Các bài viết tổng hợp kiến thức Toán 12.
Hãy truy cập Tusach.vn ngay hôm nay để học tốt môn Toán 12!
Bảng Tổng Hợp Các Công Thức Đạo Hàm Quan Trọng
| Hàm số | Đạo hàm |
|---|
| f(x) = c (hằng số) | f'(x) = 0 |
| f(x) = xn | f'(x) = nxn-1 |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |
