Giải mục 1 trang 5,6,7 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 1 trang 5,6,7 SGK Toán 12 tập 1 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 5,6,7 sách giáo khoa Toán 12 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải các bài tập trong mục, giúp các em hiểu rõ hơn về kiến thức đã học và rèn luyện kỹ năng giải toán.
Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp tài liệu học tập chất lượng và giải đáp mọi thắc mắc.
Tính đơn điệu của hàm số
LT2
Trả lời câu hỏi Luyện tập 2 trang 7 SGK Toán 12 Kết nối tri thức
Tìm các khoảng đồng biến, khoảng nghịch biến của hàm số \(y = - {x^2} + 2x + 3\).
Phương pháp giải:
Sử dụng kiến thức về định lí về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng K.
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) đồng biến trên khoảng K.
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) nghịch biến trên khoảng K.
Lời giải chi tiết:
Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \(y' = - 2x + 2,y' > 0\) với \(x \in \left( { - \infty ;1} \right)\); \(y < 0\) với \(x \in \left( {1; + \infty } \right)\).
Do đó, hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và nghịch biến trên khoảng \(\left( {1; + \infty } \right)\).
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 6 SGK Toán 12 Kết nối tri thức
Quan sát đồ thị của hàm số \(y = {x^2}\) (H.1.2)
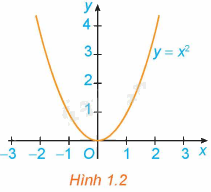
a) Hàm số đồng biến trên khoảng nào?
b) Hàm số nghịch biến trên khoảng nào?
Phương pháp giải:
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Giả sử K là một khoảng, một đoạn hoặc một nửa khoảng và \(y = f\left( x \right)\) là hàm số xác định trên K.
+ Hàm số \(y = f\left( x \right)\) được gọi là đồng biến trên K nếu \(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\)
+ Hàm số \(y = f\left( x \right)\) được gọi là nghịch biến trên K nếu \(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Lời giải chi tiết:
Từ đồ thị ta thấy:
+ Xét khoảng \(\left( {0; + \infty } \right)\): \(\forall {x_1},{x_2} \in \left( {0; + \infty } \right),{x_1} < {x_2}\) thì \(x_1^2 < x_2^2\) hay \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Suy ra, hàm số \(y = {x^2}\) đồng biến trên \(\left( {0; + \infty } \right)\).
+ Xét khoảng \(\left( { - \infty ;0} \right)\): \(\forall {x_1},{x_2} \in \left( { - \infty ;0} \right),{x_1} < {x_2}\) thì \(x_1^2 > x_2^2\)hay \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).
Suy ra, hàm số \(y = {x^2}\) nghịch biến trên \(\left( { - \infty ;0} \right)\).
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 7 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\).
a) Tính đạo hàm \(f'\left( x \right)\) và tìm các điểm x mà \(f'\left( x \right) = 0\).
b) Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.
c) Nếu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Phương pháp giải:
Cho hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\).
a) Tính đạo hàm \(f'\left( x \right)\) và tìm các điểm x mà \(f'\left( x \right) = 0\).
b) Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.
c) Nếu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
a) \(f'\left( x \right) = \left( {{x^3} - 3{x^2} + 2x + 1} \right)' = 3{x^2} - 6x + 2\)
\(f'\left( x \right) = 0 \Leftrightarrow 3{x^2} - 6x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{3 - \sqrt 3 }}{3}\\x = \frac{{3 + \sqrt 3 }}{3}\end{array} \right.\)
Vậy \(x = \frac{{3 - \sqrt 3 }}{3},x = \frac{{3 + \sqrt 3 }}{3}\) thì \(f'\left( x \right) = 0\)
b) Bảng biến thiên:
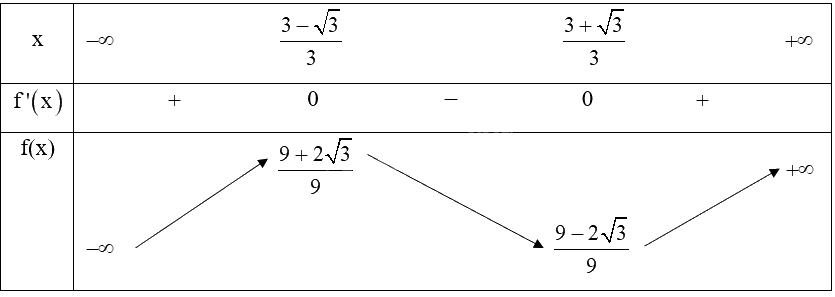
c) Hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\) đồng biến trên khoảng \(\left( { - \infty ;\frac{{3 - \sqrt 3 }}{3}} \right)\) và \(\left( {\frac{{3 + \sqrt 3 }}{3}; + \infty } \right)\).
Hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\) nghịch biến trên khoảng \(\left( {\frac{{3 - \sqrt 3 }}{3};\frac{{3 + \sqrt 3 }}{3}} \right)\).
VD1
Trả lời câu hỏi Vận dụng 1 trang 9 SGK Toán 12 Kết nối tri thức
Giải bài toán trong tình huống mở đầu bằng cách thực hiện lần lượt các yêu cầu sau:
a) Theo ý nghĩa cơ học của đạo hàm, vận tốc v(t) là đạo hàm của s(t). Hãy tìm vận tốc v(t).
b) Xét dấu của hàm v(t), từ đó suy ra câu trả lời.
Bài toán mở đầu:
Xét một chất điểm chuyển động trên một trục số nằm ngang, chiều dương từ trái sang phải (H.1.1). Giả sử vị trí s(t) (mét) của chất điểm trên trục số đã chọn tại thời điểm t (giây) được cho bởi công thức \(s\left( t \right) = {t^3} - 9{t^2} + 15t,t \ge 0\). Hỏi trong khoảng thời gian nào thì chất điểm chuyển động sang phải, trong khoảng thời gian nào thì chất điểm chuyển động sang trái?

Phương pháp giải:
a) Sử dụng kiến thức về ý nghĩa cơ học của đạo hàm để tìm hàm vận tốc: Theo ý nghĩa cơ học, vận tốc v(t) là đạo hàm của hàm số s(t).
b) Chất điểm chuyển động theo chiều dương khi \(v\left( t \right) > 0\).
Chất điểm chuyển động theo chiều âm khi \(v\left( t \right) < 0\)
Lời giải chi tiết:
a) Ta có: \(v\left( t \right) = s'\left( t \right) = \left( {{t^3} - 9{t^2} + 15t} \right)' = 3{t^2} - 18t + 15\)
b) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(v\left( t \right) > 0 \Leftrightarrow 3{t^2} - 18t + 15 > 0 \Leftrightarrow \left( {t - 1} \right)\left( {t - 5} \right) > 0 \Leftrightarrow \left[ \begin{array}{l}t < 1\\t > 5\end{array} \right.\)
\(v\left( t \right) < 0 \Leftrightarrow 3{t^2} - 18t + 15 < 0 \Leftrightarrow \left( {t - 1} \right)\left( {t - 5} \right) < 0 \Leftrightarrow 1 < t < 5\)
Chất điểm chuyển động theo chiều dương (sang bên phải) khi \(v\left( t \right) > 0\), tức là \(t \in \left( { - \infty ;1} \right) \cup \left( {5; + \infty } \right)\).
Chất điểm chuyển động theo chiều âm (sang bên trái) khi \(v\left( t \right) < 0\), tức là \(1 < t < 5\).
LT1
Trả lời câu hỏi Luyện tập 1 trang 6 SGK Toán 12 Kết nối tri thức
Hình 1.5 là đồ thị của hàm số \(y = {x^3} - 3{x^2} + 2\). Hãy tìm các khoảng đồng biến, khoảng nghịch biến của hàm số.
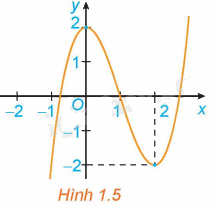
Phương pháp giải:
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến:
+ Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải.
+ Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải.
Lời giải chi tiết:
Tập xác định của hàm số là \(\mathbb{R}\).
Trong khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\) thì đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) đi lên từ trái sang phải nên hàm số \(y = {x^3} - 3{x^2} + 2\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\).
Trong khoảng \(\left( {0;2} \right)\) thì đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) đi xuống từ trái sang phải nên hàm số \(y = {x^3} - 3{x^2} + 2\) nghịch biến trên khoảng \(\left( {0;2} \right)\).
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 6 SGK Toán 12 Kết nối tri thức
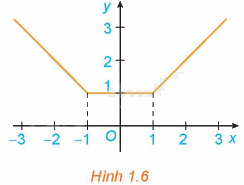
a) Xét dấu đạo hàm của hàm số trên các khoảng \(\left( { - \infty ; - 1} \right)\), \(\left( {1; + \infty } \right)\). Nêu nhận xét về mối quan hệ giữa tính đồng biến, nghịch biến và dấu của đạo hàm trên mỗi khoảng này.
b) Có nhận xét gì về đạo hàm y’ của hàm số y trên khoảng \(\left( { - 1;1} \right)\)?
Phương pháp giải:
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm nhận xét:
+ Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải.
+ Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải.
Lời giải chi tiết:
a) + Xét khoảng \(\left( { - \infty ; - 1} \right)\) ta có: \(y' = \left( { - x} \right)' = - 1 < 0\)
Trong khoảng \(\left( { - \infty ; - 1} \right)\) ta thấy hàm số y nghịch biến và đạo hàm \(y' < 0\).
+ Xét khoảng \(\left( {1; + \infty } \right)\) ta có: \(y' = x' = 1 > 0\)
Trong khoảng \(\left( {1; + \infty } \right)\) ta thấy hàm số y đồng biến và đạo hàm \(y' > 0\).
b) Trong khoảng \(\left( { - 1;1} \right)\) ta có: \(y' = \left( 1 \right)' = 0\)
Trong khoảng \(\left( { - 1;1} \right)\) ta thấy hàm số y không đổi và đạo hàm \(y' = 0\).
LT3
Trả lời câu hỏi Luyện tập 3 trang 9 SGK Toán 12 Kết nối tri thức
Tìm các khoảng đơn điệu của các hàm số sau:
a) \(y = \frac{1}{3}{x^3} + 3{x^2} + 5x + 2\);
b) \(y = \frac{{ - {x^2} + 5x - 7}}{{x - 2}}\).
Phương pháp giải:
- Sử dụng kiến thức về các bước để xét tính đơn điệu của hàm số để tìm khoảng đơn điệu của hàm số: Các bước để xét tính đơn điệu của hàm số \(y = f\left( x \right)\):
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm \(f'\left( x \right)\). Tìm các điểm \({x_i}\left( {i = 1,2,...} \right)\) mà tại đó đạo hàm bằng 0 hoặc không tồn tại.
3. Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập bảng biến thiên của hàm số.
4. Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
a) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = {x^2} + 6x + 5,y' = 0 \Leftrightarrow {x^2} + 6x + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - 5\end{array} \right.\)
Lập bảng biến thiên của hàm số:
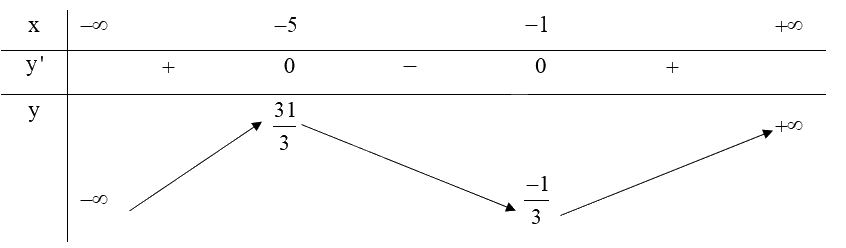
Hàm số \(y = \frac{1}{3}{x^3} + 3{x^2} + 5x + 2\) đồng biến trên khoảng \(\left( { - \infty ; - 5} \right)\) và \(\left( { - 1; + \infty } \right)\).
Hàm số \(y = \frac{1}{3}{x^3} + 3{x^2} + 5x + 2\) nghịch biến trên khoảng \(\left( { - 5; - 1} \right)\).
b) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).
Ta có: \(y' = \frac{{\left( { - 2x + 5} \right)\left( {x - 2} \right) - \left( { - {x^2} + 5x - 7} \right)}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{ - {x^2} + 4x - 3}}{{{{\left( {x - 2} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\) (thỏa mãn)
Lập bảng biến thiên của hàm số:
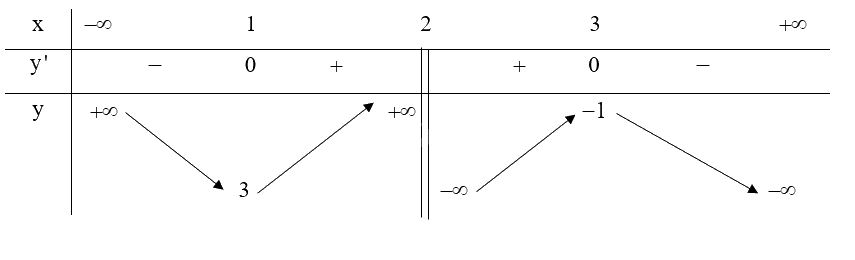 Hàm số \(y = \frac{{ - {x^2} + 5x - 7}}{{x - 2}}\) đồng biến trên khoảng \(\left( {1;2} \right)\) và \(\left( {2;3} \right)\).
Hàm số \(y = \frac{{ - {x^2} + 5x - 7}}{{x - 2}}\) đồng biến trên khoảng \(\left( {1;2} \right)\) và \(\left( {2;3} \right)\).
Hàm số \(y = \frac{{ - {x^2} + 5x - 7}}{{x - 2}}\) nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {3; + \infty } \right)\).
- HĐ1
- LT1
- HĐ2
- LT2
- HĐ3
- LT3
- VD1
Trả lời câu hỏi Hoạt động 1 trang 6 SGK Toán 12 Kết nối tri thức
Quan sát đồ thị của hàm số \(y = {x^2}\) (H.1.2)
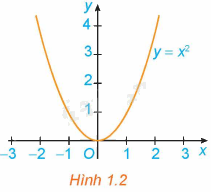
a) Hàm số đồng biến trên khoảng nào?
b) Hàm số nghịch biến trên khoảng nào?
Phương pháp giải:
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Giả sử K là một khoảng, một đoạn hoặc một nửa khoảng và \(y = f\left( x \right)\) là hàm số xác định trên K.
+ Hàm số \(y = f\left( x \right)\) được gọi là đồng biến trên K nếu \(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\)
+ Hàm số \(y = f\left( x \right)\) được gọi là nghịch biến trên K nếu \(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Lời giải chi tiết:
Từ đồ thị ta thấy:
+ Xét khoảng \(\left( {0; + \infty } \right)\): \(\forall {x_1},{x_2} \in \left( {0; + \infty } \right),{x_1} < {x_2}\) thì \(x_1^2 < x_2^2\) hay \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Suy ra, hàm số \(y = {x^2}\) đồng biến trên \(\left( {0; + \infty } \right)\).
+ Xét khoảng \(\left( { - \infty ;0} \right)\): \(\forall {x_1},{x_2} \in \left( { - \infty ;0} \right),{x_1} < {x_2}\) thì \(x_1^2 > x_2^2\)hay \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).
Suy ra, hàm số \(y = {x^2}\) nghịch biến trên \(\left( { - \infty ;0} \right)\).
Trả lời câu hỏi Luyện tập 1 trang 6 SGK Toán 12 Kết nối tri thức
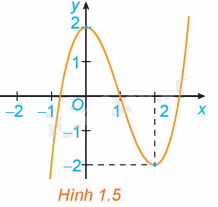
Hình 1.5 là đồ thị của hàm số \(y = {x^3} - 3{x^2} + 2\). Hãy tìm các khoảng đồng biến, khoảng nghịch biến của hàm số.
Phương pháp giải:
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến:
+ Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải.
+ Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải.
Lời giải chi tiết:
Tập xác định của hàm số là \(\mathbb{R}\).
Trong khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\) thì đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) đi lên từ trái sang phải nên hàm số \(y = {x^3} - 3{x^2} + 2\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\).
Trong khoảng \(\left( {0;2} \right)\) thì đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) đi xuống từ trái sang phải nên hàm số \(y = {x^3} - 3{x^2} + 2\) nghịch biến trên khoảng \(\left( {0;2} \right)\).
Trả lời câu hỏi Hoạt động 2 trang 6 SGK Toán 12 Kết nối tri thức
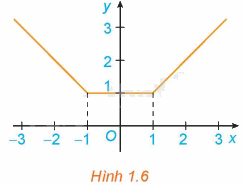
a) Xét dấu đạo hàm của hàm số trên các khoảng \(\left( { - \infty ; - 1} \right)\), \(\left( {1; + \infty } \right)\). Nêu nhận xét về mối quan hệ giữa tính đồng biến, nghịch biến và dấu của đạo hàm trên mỗi khoảng này.
b) Có nhận xét gì về đạo hàm y’ của hàm số y trên khoảng \(\left( { - 1;1} \right)\)?
Phương pháp giải:
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm nhận xét:
+ Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải.
+ Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải.
Lời giải chi tiết:
a) + Xét khoảng \(\left( { - \infty ; - 1} \right)\) ta có: \(y' = \left( { - x} \right)' = - 1 < 0\)
Trong khoảng \(\left( { - \infty ; - 1} \right)\) ta thấy hàm số y nghịch biến và đạo hàm \(y' < 0\).
+ Xét khoảng \(\left( {1; + \infty } \right)\) ta có: \(y' = x' = 1 > 0\)
Trong khoảng \(\left( {1; + \infty } \right)\) ta thấy hàm số y đồng biến và đạo hàm \(y' > 0\).
b) Trong khoảng \(\left( { - 1;1} \right)\) ta có: \(y' = \left( 1 \right)' = 0\)
Trong khoảng \(\left( { - 1;1} \right)\) ta thấy hàm số y không đổi và đạo hàm \(y' = 0\).
Trả lời câu hỏi Luyện tập 2 trang 7 SGK Toán 12 Kết nối tri thức
Tìm các khoảng đồng biến, khoảng nghịch biến của hàm số \(y = - {x^2} + 2x + 3\).
Phương pháp giải:
Sử dụng kiến thức về định lí về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng K.
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) đồng biến trên khoảng K.
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) nghịch biến trên khoảng K.
Lời giải chi tiết:
Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \(y' = - 2x + 2,y' > 0\) với \(x \in \left( { - \infty ;1} \right)\); \(y < 0\) với \(x \in \left( {1; + \infty } \right)\).
Do đó, hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và nghịch biến trên khoảng \(\left( {1; + \infty } \right)\).
Trả lời câu hỏi Hoạt động 3 trang 7 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\).
a) Tính đạo hàm \(f'\left( x \right)\) và tìm các điểm x mà \(f'\left( x \right) = 0\).
b) Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.
c) Nếu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Phương pháp giải:
Cho hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\).
a) Tính đạo hàm \(f'\left( x \right)\) và tìm các điểm x mà \(f'\left( x \right) = 0\).
b) Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.
c) Nếu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
a) \(f'\left( x \right) = \left( {{x^3} - 3{x^2} + 2x + 1} \right)' = 3{x^2} - 6x + 2\)
\(f'\left( x \right) = 0 \Leftrightarrow 3{x^2} - 6x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{3 - \sqrt 3 }}{3}\\x = \frac{{3 + \sqrt 3 }}{3}\end{array} \right.\)
Vậy \(x = \frac{{3 - \sqrt 3 }}{3},x = \frac{{3 + \sqrt 3 }}{3}\) thì \(f'\left( x \right) = 0\)
b) Bảng biến thiên:
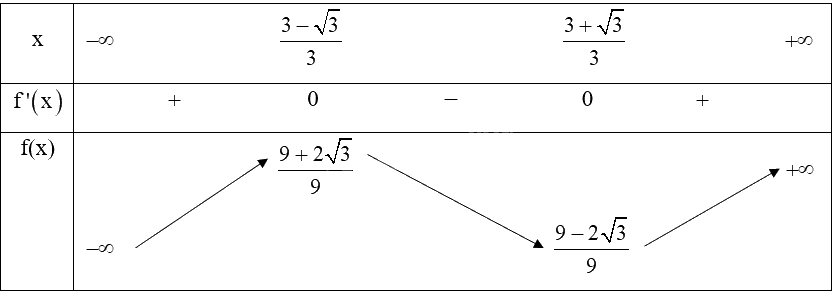
c) Hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\) đồng biến trên khoảng \(\left( { - \infty ;\frac{{3 - \sqrt 3 }}{3}} \right)\) và \(\left( {\frac{{3 + \sqrt 3 }}{3}; + \infty } \right)\).
Hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\) nghịch biến trên khoảng \(\left( {\frac{{3 - \sqrt 3 }}{3};\frac{{3 + \sqrt 3 }}{3}} \right)\).
Trả lời câu hỏi Luyện tập 3 trang 9 SGK Toán 12 Kết nối tri thức
Tìm các khoảng đơn điệu của các hàm số sau:
a) \(y = \frac{1}{3}{x^3} + 3{x^2} + 5x + 2\);
b) \(y = \frac{{ - {x^2} + 5x - 7}}{{x - 2}}\).
Phương pháp giải:
- Sử dụng kiến thức về các bước để xét tính đơn điệu của hàm số để tìm khoảng đơn điệu của hàm số: Các bước để xét tính đơn điệu của hàm số \(y = f\left( x \right)\):
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm \(f'\left( x \right)\). Tìm các điểm \({x_i}\left( {i = 1,2,...} \right)\) mà tại đó đạo hàm bằng 0 hoặc không tồn tại.
3. Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập bảng biến thiên của hàm số.
4. Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
a) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = {x^2} + 6x + 5,y' = 0 \Leftrightarrow {x^2} + 6x + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - 5\end{array} \right.\)
Lập bảng biến thiên của hàm số:
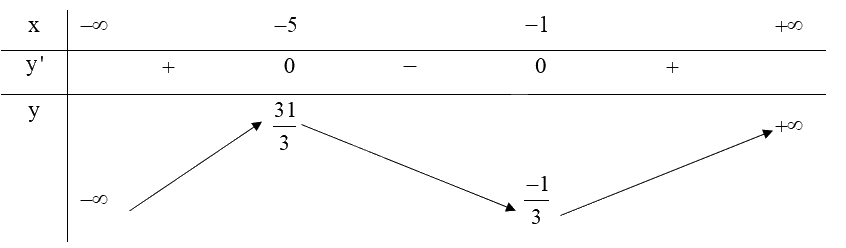
Hàm số \(y = \frac{1}{3}{x^3} + 3{x^2} + 5x + 2\) đồng biến trên khoảng \(\left( { - \infty ; - 5} \right)\) và \(\left( { - 1; + \infty } \right)\).
Hàm số \(y = \frac{1}{3}{x^3} + 3{x^2} + 5x + 2\) nghịch biến trên khoảng \(\left( { - 5; - 1} \right)\).
b) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).
Ta có: \(y' = \frac{{\left( { - 2x + 5} \right)\left( {x - 2} \right) - \left( { - {x^2} + 5x - 7} \right)}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{ - {x^2} + 4x - 3}}{{{{\left( {x - 2} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\) (thỏa mãn)
Lập bảng biến thiên của hàm số:
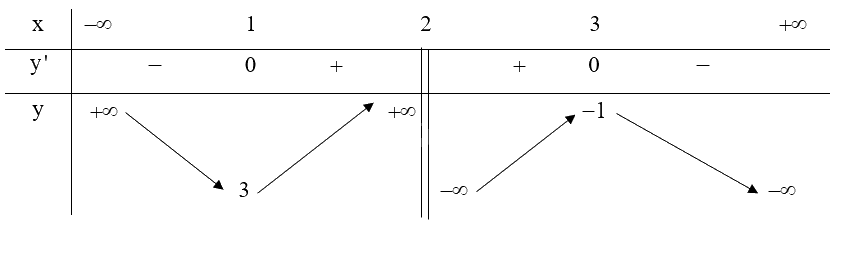 Hàm số \(y = \frac{{ - {x^2} + 5x - 7}}{{x - 2}}\) đồng biến trên khoảng \(\left( {1;2} \right)\) và \(\left( {2;3} \right)\).
Hàm số \(y = \frac{{ - {x^2} + 5x - 7}}{{x - 2}}\) đồng biến trên khoảng \(\left( {1;2} \right)\) và \(\left( {2;3} \right)\).
Hàm số \(y = \frac{{ - {x^2} + 5x - 7}}{{x - 2}}\) nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {3; + \infty } \right)\).
Trả lời câu hỏi Vận dụng 1 trang 9 SGK Toán 12 Kết nối tri thức
Giải bài toán trong tình huống mở đầu bằng cách thực hiện lần lượt các yêu cầu sau:
a) Theo ý nghĩa cơ học của đạo hàm, vận tốc v(t) là đạo hàm của s(t). Hãy tìm vận tốc v(t).
b) Xét dấu của hàm v(t), từ đó suy ra câu trả lời.
Bài toán mở đầu:
Xét một chất điểm chuyển động trên một trục số nằm ngang, chiều dương từ trái sang phải (H.1.1). Giả sử vị trí s(t) (mét) của chất điểm trên trục số đã chọn tại thời điểm t (giây) được cho bởi công thức \(s\left( t \right) = {t^3} - 9{t^2} + 15t,t \ge 0\). Hỏi trong khoảng thời gian nào thì chất điểm chuyển động sang phải, trong khoảng thời gian nào thì chất điểm chuyển động sang trái?

Phương pháp giải:
a) Sử dụng kiến thức về ý nghĩa cơ học của đạo hàm để tìm hàm vận tốc: Theo ý nghĩa cơ học, vận tốc v(t) là đạo hàm của hàm số s(t).
b) Chất điểm chuyển động theo chiều dương khi \(v\left( t \right) > 0\).
Chất điểm chuyển động theo chiều âm khi \(v\left( t \right) < 0\)
Lời giải chi tiết:
a) Ta có: \(v\left( t \right) = s'\left( t \right) = \left( {{t^3} - 9{t^2} + 15t} \right)' = 3{t^2} - 18t + 15\)
b) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(v\left( t \right) > 0 \Leftrightarrow 3{t^2} - 18t + 15 > 0 \Leftrightarrow \left( {t - 1} \right)\left( {t - 5} \right) > 0 \Leftrightarrow \left[ \begin{array}{l}t < 1\\t > 5\end{array} \right.\)
\(v\left( t \right) < 0 \Leftrightarrow 3{t^2} - 18t + 15 < 0 \Leftrightarrow \left( {t - 1} \right)\left( {t - 5} \right) < 0 \Leftrightarrow 1 < t < 5\)
Chất điểm chuyển động theo chiều dương (sang bên phải) khi \(v\left( t \right) > 0\), tức là \(t \in \left( { - \infty ;1} \right) \cup \left( {5; + \infty } \right)\).
Chất điểm chuyển động theo chiều âm (sang bên trái) khi \(v\left( t \right) < 0\), tức là \(1 < t < 5\).
Giải mục 1 trang 5,6,7 SGK Toán 12 tập 1 - Kết nối tri thức: Tổng quan và Hướng dẫn chi tiết
Mục 1 của SGK Toán 12 tập 1 chương trình Kết nối tri thức tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số và đồ thị. Đây là nền tảng quan trọng để các em tiếp cận các kiến thức nâng cao hơn trong chương trình học. Việc nắm vững các khái niệm, định lý và kỹ năng giải bài tập trong mục này là vô cùng cần thiết.
Nội dung chính của Mục 1
- Ôn tập về hàm số: Các loại hàm số (hàm số bậc nhất, hàm số bậc hai, hàm số mũ, hàm số logarit), tập xác định, tập giá trị, tính đơn điệu, cực trị.
- Đồ thị hàm số: Cách vẽ đồ thị hàm số, các tính chất của đồ thị, ứng dụng của đồ thị trong việc giải quyết các bài toán.
- Phương trình và bất phương trình: Giải phương trình và bất phương trình chứa hàm số, ứng dụng của phương trình và bất phương trình trong thực tế.
Giải chi tiết các bài tập trang 5,6,7
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1 trang 5,6,7 SGK Toán 12 tập 1 Kết nối tri thức:
Bài 1.1 (Trang 5)
Đề bài: ... (Nội dung đề bài)
Lời giải: ... (Lời giải chi tiết, bao gồm các bước giải, giải thích rõ ràng và sử dụng các công thức liên quan). Ví dụ:
- Bước 1: Xác định tập xác định của hàm số.
- Bước 2: Tính đạo hàm của hàm số.
- Bước 3: Tìm các điểm cực trị của hàm số.
- Bước 4: Lập bảng biến thiên của hàm số.
- Bước 5: Kết luận về tính đơn điệu và cực trị của hàm số.
Bài 1.2 (Trang 6)
Đề bài: ... (Nội dung đề bài)
Lời giải: ... (Lời giải chi tiết)
Bài 1.3 (Trang 7)
Đề bài: ... (Nội dung đề bài)
Lời giải: ... (Lời giải chi tiết)
Mẹo giải bài tập hiệu quả
- Nắm vững kiến thức cơ bản: Hiểu rõ các khái niệm, định lý và công thức liên quan đến hàm số và đồ thị.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Sử dụng công cụ hỗ trợ: Sử dụng máy tính bỏ túi hoặc các phần mềm vẽ đồ thị để kiểm tra kết quả và hiểu rõ hơn về đồ thị hàm số.
- Tham khảo các nguồn tài liệu khác: Đọc thêm sách tham khảo, xem video bài giảng hoặc tìm kiếm trên internet để bổ sung kiến thức.
Kết luận
Hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập trong mục 1 trang 5,6,7 SGK Toán 12 tập 1 Kết nối tri thức, các em sẽ tự tin hơn trong việc học tập và đạt kết quả tốt nhất. Tusach.vn sẽ tiếp tục đồng hành cùng các em trong suốt quá trình học tập. Chúc các em thành công!
| Bài tập | Độ khó | Lời giải |
|---|---|---|
| 1.1 | Trung bình | Xem lời giải |
| 1.2 | Khó | Xem lời giải |
| 1.3 | Dễ | Xem lời giải |