Lý thuyết Phương trình mặt cầu Toán 12 Kết nối tri thức
Tổng quan nội dung
Lý Thuyết Phương Trình Mặt Cầu Toán 12 Kết Nối Tri Thức
Phương trình mặt cầu là một trong những kiến thức quan trọng trong chương trình Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp cho bạn một cách đầy đủ và chi tiết về lý thuyết, công thức và các dạng bài tập thường gặp liên quan đến phương trình mặt cầu.
Nắm vững kiến thức này sẽ giúp bạn giải quyết các bài toán trong kỳ thi THPT Quốc gia một cách hiệu quả.
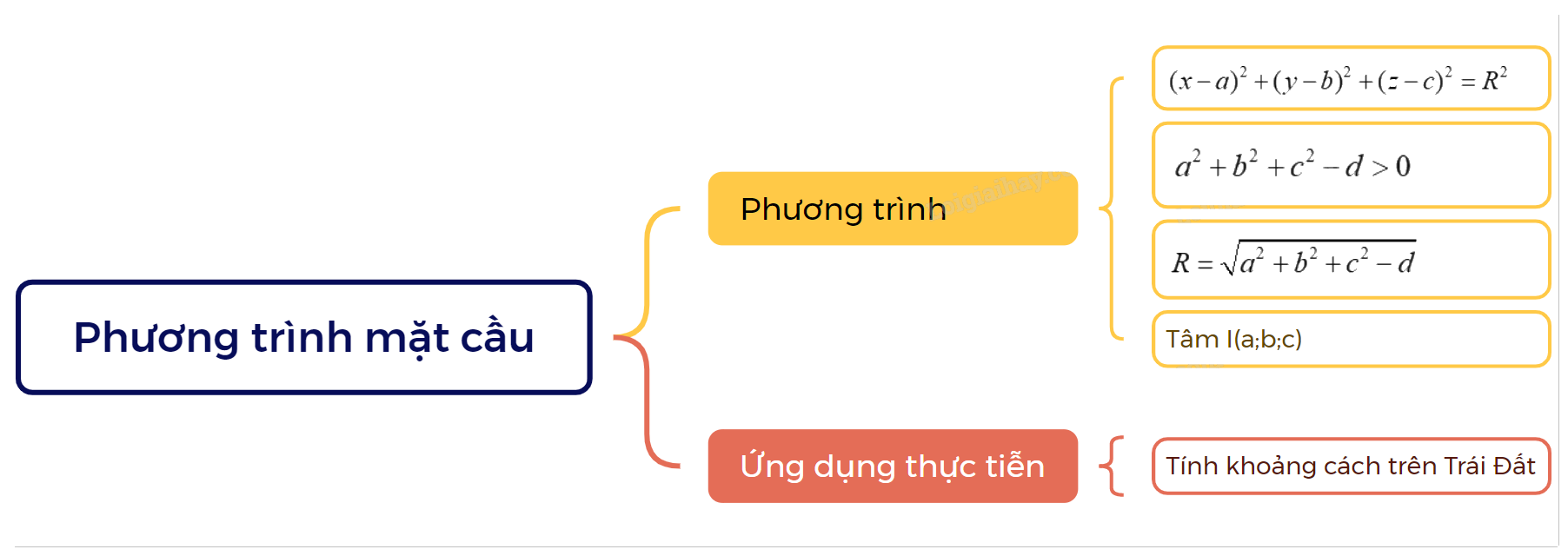
1. Phương trình mặt cầu
1. Phương trình mặt cầu
Trong không gian Oxyz, mặt cầu (S) tâm I(a;b;c) bán kính R có phương trình \({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {R^2}\) |
Nhận xét: Với a, b, c là các hằng số, phương trình \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) có thể viết lại thành \({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {a^2} + {b^2} + {c^2} - d\) và là phương trình của một mặt cầu (S) khi và chỉ khi \({a^2} + {b^2} + {c^2} - d > 0\). Khi đó, (S) có tâm I(a;b;c) và bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \).
2. Một số ứng dụng của phương trình mặt cầu trong thực tiễn
Ví dụ: Biết rằng nếu vị trí M có vĩ độ và kinh độ tương ứng là \({\alpha ^ \circ }N,{\beta ^ \circ }E(0 < \alpha ,\beta < 90)\) thì có tọa độ \(M(\cos {\alpha ^ \circ }\cos {\beta ^ \circ };\cos {\alpha ^ \circ }\sin {\beta ^ \circ };\sin {\alpha ^ \circ })\). Tính khoảng cách trên mặt đất từ vị trí P: \({10^ \circ }N,{15^ \circ }E\) đến vị trí Q: \({80^ \circ }N,{70^ \circ }E\).
Giải:
Ta có: \(P(\cos {10^ \circ }\cos {15^ \circ };\cos {10^ \circ }\sin {15^ \circ };\sin {10^ \circ })\), \(Q(\cos {80^ \circ }\cos {70^ \circ };\cos {80^ \circ }\sin {70^ \circ };\sin {80^ \circ })\).
Suy ra: \(\overrightarrow {OP} = (\cos {10^ \circ }\cos {15^ \circ };\cos {10^ \circ }\sin {15^ \circ };\sin {10^ \circ })\), \(\overrightarrow {OQ} = (\cos {80^ \circ }\cos {70^ \circ };\cos {80^ \circ }\sin {70^ \circ };\sin {80^ \circ })\).
Do đó,
\(\overrightarrow {OP} .\overrightarrow {OQ} = \cos {10^ \circ }\cos {15^ \circ }\cos {80^ \circ }\cos {70^ \circ } + \cos {10^ \circ }\sin {15^ \circ }\cos {80^ \circ }\sin {70^ \circ } + \sin {10^ \circ }\sin {80^ \circ } \approx 0,2691\).
Vì P, Q thuộc mặt đất nên \(\left| {\overrightarrow {OP} } \right| = \left| {\overrightarrow {OQ} } \right| = 1\).
Do đó \(\cos \widehat {POQ} = \frac{{\overrightarrow {OP} .\overrightarrow {OQ} }}{{\left| {\overrightarrow {OP} } \right|.\left| {\overrightarrow {OQ} } \right|}} \approx 0,2691.\) Suy ra, \(\widehat {POQ} \approx 74,{3893^ \circ }\).
Mặt khác, đường tròn tâm O, đi qua P, Q có bán kính 1 và chu vi là \(2\pi \approx 6,2832\), nên cung nhỏ của đường tròn đó có độ dài xấp xỉ bằng \(\frac{{74,3893}}{{360}}.6,2832 \approx 1,2983\).
Do 1 đơn vị dài trong không gian Oxyz tương ứng với 6371 km trên thực tế, nên khoảng cách trên mặt đất giữa hai vị trí P, Q xấp xỉ bằng 1,2983.6371 = 8271,4693 (km).
Lý Thuyết Phương Trình Mặt Cầu Toán 12 Kết Nối Tri Thức: Tổng Quan
Phương trình mặt cầu là một phần quan trọng của hình học không gian trong chương trình Toán 12 Kết nối tri thức. Hiểu rõ lý thuyết và cách áp dụng sẽ giúp học sinh giải quyết các bài toán một cách chính xác và hiệu quả. Bài viết này sẽ cung cấp một cái nhìn tổng quan về phương trình mặt cầu, bao gồm định nghĩa, phương trình chính tắc, phương trình tổng quát, và các ứng dụng thực tế.
1. Định Nghĩa Mặt Cầu
Mặt cầu là tập hợp tất cả các điểm trong không gian cách một điểm cố định (gọi là tâm) một khoảng không đổi (gọi là bán kính).
2. Phương Trình Chính Tắc của Mặt Cầu
Trong không gian với hệ tọa độ Oxyz, phương trình chính tắc của mặt cầu có tâm I(a; b; c) và bán kính R được viết như sau:
(x - a)2 + (y - b)2 + (z - c)2 = R2
3. Phương Trình Tổng Quát của Mặt Cầu
Phương trình tổng quát của mặt cầu có dạng:
x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0
Với điều kiện: a2 + b2 + c2 - d > 0
Tâm của mặt cầu là I(a; b; c) và bán kính R = √(a2 + b2 + c2 - d)
4. Các Dạng Bài Tập Thường Gặp
- Dạng 1: Xác định tâm và bán kính của mặt cầu khi cho phương trình.
- Dạng 2: Viết phương trình mặt cầu khi biết tâm và bán kính.
- Dạng 3: Xác định điều kiện để phương trình là phương trình của mặt cầu.
- Dạng 4: Bài toán liên quan đến khoảng cách từ một điểm đến mặt cầu.
- Dạng 5: Bài toán về giao tuyến của mặt cầu và đường thẳng/mặt phẳng.
5. Ví Dụ Minh Họa
Ví dụ 1: Xác định tâm và bán kính của mặt cầu có phương trình (x - 1)2 + (y + 2)2 + (z - 3)2 = 9
Giải: Tâm của mặt cầu là I(1; -2; 3) và bán kính R = √9 = 3
Ví dụ 2: Viết phương trình mặt cầu có tâm I(0; 0; 0) và bán kính R = 5
Giải: Phương trình mặt cầu là x2 + y2 + z2 = 25
6. Mẹo Giải Bài Tập
- Luôn kiểm tra điều kiện để phương trình là phương trình của mặt cầu (a2 + b2 + c2 - d > 0).
- Sử dụng các công thức liên quan đến khoảng cách để giải các bài toán về khoảng cách từ một điểm đến mặt cầu.
- Vẽ hình để hình dung rõ hơn về bài toán, đặc biệt là các bài toán về giao tuyến.
7. Luyện Tập Thêm
Để nắm vững kiến thức về phương trình mặt cầu, bạn nên luyện tập thêm nhiều bài tập khác nhau. Bạn có thể tìm thấy các bài tập trong sách giáo khoa, sách bài tập, hoặc trên các trang web học toán trực tuyến như tusach.vn.
8. Kết Luận
Lý thuyết phương trình mặt cầu Toán 12 Kết nối tri thức là một phần quan trọng của chương trình học. Việc nắm vững kiến thức này không chỉ giúp bạn giải quyết các bài toán trong kỳ thi THPT Quốc gia mà còn là nền tảng cho việc học tập các môn học khác liên quan đến hình học không gian. Hãy dành thời gian ôn tập và luyện tập để đạt kết quả tốt nhất!