Giải bài tập 5.24 trang 53 SGK Toán 12 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 5.24 Trang 53 Toán 12 Tập 2 - Kết Nối Tri Thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 12 tập 2 - Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn giải bài tập 5.24 trang 53 một cách dễ hiểu nhất.
Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
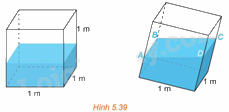
(H.5.39) Trong một bể hình lập phương cạnh 1m có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành ABCD và khoảng cách từ các điểm A, B, C đến đáy bể tương ứng là 40cm, 44cm, 48cm. a) Khoảng cách từ điểm D đến đáy bể bằng bao nhiêu centimét? (Tính gần đúng, lấy giá trị nguyên.) b) Đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ?
Đề bài
(H.5.39) Trong một bể hình lập phương cạnh 1m có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành ABCD và khoảng cách từ các điểm A, B, C đến đáy bể tương ứng là 40cm, 44cm, 48cm.
a) Khoảng cách từ điểm D đến đáy bể bằng bao nhiêu centimét? (Tính gần đúng, lấy giá trị nguyên.)
b) Đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ?
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\). Khi đó, góc giữa (P) và (Q), kí hiệu là ((P), (Q)) được tính theo công thức:
\(\cos \left( {\left( P \right),\left( Q \right)} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {AA' + BB' + CC'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {A{'^2} + B{'^2} + C{'^2}} }}\)
Lời giải chi tiết
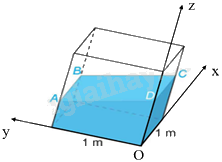
a) Chọn hệ trục tọa độ Oxyz như hình vẽ.
Khi đó, \(A\left( {0;1;0,4} \right),B\left( {1;1;0,44} \right),C\left( {1;0;0,48} \right),D\left( {0;0;z} \right)\)
Suy ra: \(\overrightarrow {AB} \left( {1;0;0,04} \right),\overrightarrow {DC} \left( {1;0,0,48 - z} \right)\)
Vì ABCD là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \Rightarrow 0,48 - z = 0,04 \Rightarrow z = 0,44\)
Do đó, \(D\left( {0;0;0,44} \right)\). Vậy khoảng cách từ D đến đáy bể bằng 44cm.
b) Đặt tên các điểm như hình vẽ. Kẻ AA’ vuông góc với Oz tại A’.
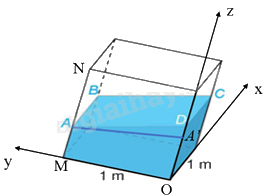
Mặt phẳng (Oxz) nhận \(\overrightarrow j \left( {0;1;0} \right)\) làm vectơ pháp tuyến nên phương trình mặt phẳng (Oxz) là: \(y = 0\).
Ta có: \(AA' = d\left( {A,\left( {Oxz} \right)} \right) = \frac{{\left| 1 \right|}}{{\sqrt 1 }} = 1\), \(AD = \sqrt {{1^2} + 0,{{04}^2}} = \frac{{\sqrt {626} }}{{25}}\)
Tam giác ADA’ vuông tại A’ nên \(\cos \left( {AA',DA} \right) = \frac{{AA'}}{{AD}} = \frac{1}{{\frac{{\sqrt {626} }}{{25}}}} \Rightarrow \left( {AA',AD} \right) \approx 2,{3^o}\)
Vậy đáy bể nghiêng mới mặt nằm ngang một góc khoảng \(2,{3^o}\).
Giải Bài Tập 5.24 Trang 53 Toán 12 Tập 2 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 5.24 trang 53 SGK Toán 12 tập 2 Kết nối tri thức thuộc chương trình học về Nguyên hàm của hàm số. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về nguyên hàm, tích phân để giải quyết các bài toán thực tế.
Đề Bài Bài Tập 5.24 Trang 53 Toán 12 Tập 2 - Kết Nối Tri Thức
(Đề bài sẽ được chèn vào đây - ví dụ: Tính tích phân ∫(x^2 + 1)dx từ 0 đến 1)
Lời Giải Chi Tiết Bài Tập 5.24 Trang 53 Toán 12 Tập 2 - Kết Nối Tri Thức
Để giải bài tập này, chúng ta cần thực hiện các bước sau:
- Bước 1: Xác định nguyên hàm của hàm số. Nguyên hàm của hàm số f(x) là hàm số F(x) sao cho F'(x) = f(x).
- Bước 2: Tính giá trị của nguyên hàm tại cận trên và cận dưới.
- Bước 3: Lấy hiệu giữa giá trị nguyên hàm tại cận trên và cận dưới. Kết quả thu được là giá trị của tích phân xác định.
Ví dụ minh họa:
Giả sử đề bài là: Tính tích phân ∫(x^2 + 1)dx từ 0 đến 1.
- Nguyên hàm của x^2 + 1 là (x^3)/3 + x.
- Giá trị của nguyên hàm tại x = 1 là (1^3)/3 + 1 = 4/3.
- Giá trị của nguyên hàm tại x = 0 là (0^3)/3 + 0 = 0.
- Vậy, tích phân ∫(x^2 + 1)dx từ 0 đến 1 là 4/3 - 0 = 4/3.
Các Dạng Bài Tập Tương Tự
Ngoài bài tập 5.24, chương này còn nhiều bài tập tương tự yêu cầu học sinh:
- Tính tích phân xác định của các hàm số đơn giản.
- Tính tích phân xác định bằng phương pháp đổi biến.
- Tính tích phân xác định bằng phương pháp tích phân từng phần.
Mẹo Giải Bài Tập Nguyên Hàm và Tích Phân
Để giải tốt các bài tập về nguyên hàm và tích phân, bạn nên:
- Nắm vững các công thức nguyên hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các kỹ thuật giải bài tập.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm tính toán.
Tài Liệu Tham Khảo
Để hiểu sâu hơn về nguyên hàm và tích phân, bạn có thể tham khảo:
- Sách giáo khoa Toán 12 tập 2 - Kết nối tri thức.
- Sách bài tập Toán 12 tập 2 - Kết nối tri thức.
- Các trang web học toán trực tuyến uy tín.
Hy vọng bài giải chi tiết này sẽ giúp bạn hiểu rõ hơn về bài tập 5.24 trang 53 SGK Toán 12 tập 2 - Kết nối tri thức. Chúc bạn học tốt!
Lưu ý: Bài giải trên chỉ mang tính chất tham khảo. Bạn nên tự mình giải bài tập để hiểu rõ hơn về kiến thức và rèn luyện kỹ năng giải toán.