Lý thuyết Khoảng biến thiên và khoảng tứ phân vị Toán 12 Kết nối tri thức
Tổng quan nội dung
Lý thuyết Khoảng biến thiên và khoảng tứ phân vị Toán 12 Kết nối tri thức
Khoảng biến thiên và khoảng tứ phân vị là những khái niệm quan trọng trong thống kê, giúp đo lường mức độ phân tán của một tập dữ liệu.
Trong chương trình Toán 12 Kết nối tri thức, việc nắm vững lý thuyết này là nền tảng để giải quyết các bài toán thực tế và chuẩn bị cho kỳ thi tốt nghiệp THPT.
1. Khoảng biến thiên
1. Khoảng biến thiên
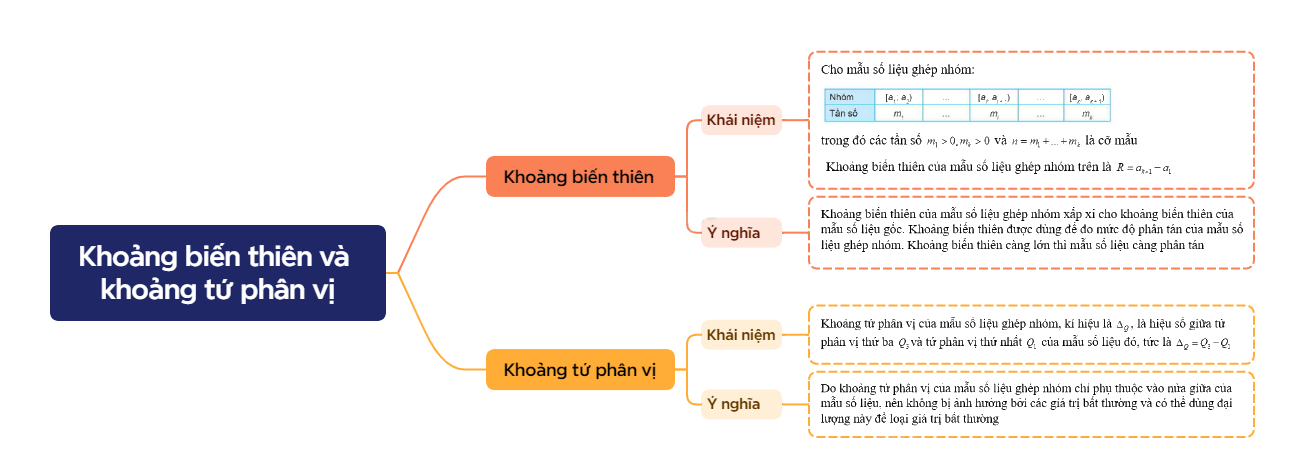
Cho mẫu số liệu ghép nhóm:

trong đó các tần số \({m_1} > 0,{m_k} > 0\) và \(n = {m_1} + ... + {m_k}\) là cỡ mẫu
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là \(R = {a_{k + 1}} - {a_1}\) |
Ý nghĩa: Khoảng biến thiên của mẫu số liệu ghép nhóm xấp xỉ cho khoảng biến thiên của mẫu số liệu gốc. Khoảng biến thiên được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán
2. Khoảng tứ phân vị
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu là \({\Delta _Q}\), là hiệu số giữa tứ phân vị thứ ba \({Q_3}\)và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\) |
Ý nghĩa: Do khoảng tứ phân vị của mẫu số liệu ghép nhóm chỉ phụ thuộc vào nửa giữa của mẫu số liệu, nên không bị ảnh hưởng bởi các giá trị bất thường và có thể dùng đại lượng này để loại giá trị bất thường
Lý Thuyết Khoảng Biến Thiên và Khoảng Tứ Phân Vị Toán 12 Kết Nối Tri Thức
Trong chương trình Toán 12 Kết nối tri thức, thống kê đóng vai trò quan trọng, và việc hiểu rõ về khoảng biến thiên và khoảng tứ phân vị là nền tảng để phân tích dữ liệu. Bài viết này sẽ cung cấp một cái nhìn chi tiết về lý thuyết này, kèm theo ví dụ minh họa và bài tập để bạn có thể nắm vững kiến thức.
1. Khoảng Biến Thiên (Range)
Khoảng biến thiên là hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất trong một tập dữ liệu. Nó cho biết mức độ trải rộng của dữ liệu.
Công thức:
R = Xmax - Xmin
Trong đó:
- R: Khoảng biến thiên
- Xmax: Giá trị lớn nhất trong tập dữ liệu
- Xmin: Giá trị nhỏ nhất trong tập dữ liệu
Ví dụ: Cho tập dữ liệu: 2, 5, 8, 11, 15. Khoảng biến thiên là 15 - 2 = 13.
2. Khoảng Tứ Phân Vị (Quartile Range)
Khoảng tứ phân vị là hiệu giữa tứ phân vị thứ ba (Q3) và tứ phân vị thứ nhất (Q1). Nó đo lường mức độ phân tán của 50% dữ liệu trung tâm.
Công thức:
IQR = Q3 - Q1
Để tính Q1 và Q3, ta cần sắp xếp dữ liệu theo thứ tự tăng dần.
- Q1: Giá trị phân chia tập dữ liệu thành hai phần, sao cho 25% dữ liệu nhỏ hơn hoặc bằng Q1.
- Q3: Giá trị phân chia tập dữ liệu thành hai phần, sao cho 75% dữ liệu nhỏ hơn hoặc bằng Q3.
Ví dụ: Cho tập dữ liệu: 3, 7, 10, 12, 15, 18, 20.
- Sắp xếp dữ liệu: 3, 7, 10, 12, 15, 18, 20
- Q1 là giá trị thứ 2 (7)
- Q3 là giá trị thứ 5 (15)
- IQR = 15 - 7 = 8
3. Ý Nghĩa của Khoảng Biến Thiên và Khoảng Tứ Phân Vị
Khoảng biến thiên và khoảng tứ phân vị cung cấp thông tin quan trọng về sự phân tán của dữ liệu:
- Khoảng biến thiên lớn: Dữ liệu phân tán rộng, có sự khác biệt lớn giữa các giá trị.
- Khoảng biến thiên nhỏ: Dữ liệu tập trung gần nhau, có sự đồng nhất cao.
- Khoảng tứ phân vị lớn: 50% dữ liệu trung tâm phân tán rộng.
- Khoảng tứ phân vị nhỏ: 50% dữ liệu trung tâm tập trung gần nhau.
4. Bài Tập Vận Dụng
Bài 1: Tính khoảng biến thiên và khoảng tứ phân vị cho tập dữ liệu sau: 1, 4, 6, 8, 10, 12, 15.
Bài 2: Giải thích ý nghĩa của khoảng biến thiên và khoảng tứ phân vị trong bài 1.
5. Kết Luận
Lý thuyết về khoảng biến thiên và khoảng tứ phân vị là công cụ hữu ích để phân tích và hiểu rõ hơn về sự phân tán của dữ liệu. Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết các bài toán thống kê một cách hiệu quả và chính xác trong chương trình Toán 12 Kết nối tri thức và các ứng dụng thực tế.
Hãy luyện tập thêm nhiều bài tập để củng cố kiến thức và nâng cao kỹ năng giải quyết vấn đề của bạn. Chúc bạn học tốt!