Giải mục 1 trang 60, 61 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 1 trang 60, 61 SGK Toán 12 tập 1 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 60, 61 sách giáo khoa Toán 12 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em hiểu rõ hơn về nội dung bài học và tự tin giải các bài tập liên quan.
tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Hệ trục tọa độ trong không gian
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 60 SGK Toán 12 Kết nối tri thức
Trong không gian, xét ba trục Ox, Oy, Oz có chung gốc O và đôi một vuông góc với nhau. Gọi \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) là các vectơ đơn vị trên các trục đó (H.2.35).
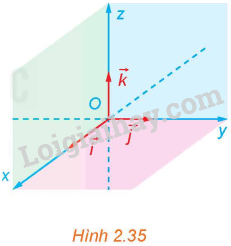
a) Gọi tên các mặt phẳng tọa độ có trong Hình 2.35.
b) Các mặt phẳng tọa độ trong Hình 2.35 có đôi một vuông góc với nhau không?
Phương pháp giải:
Sử dụng kiến thức về hai mặt phẳng vuông góc để chứng minh: Nếu mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia thì hai mặt phẳng đó vuông góc với nhau.
Lời giải chi tiết:
a) Các mặt phẳng có trong hình vẽ là: Mặt phẳng (Oxy), (Oyz), (Ozx).
b) Vì \(Ox \bot Oy,Oy \bot Oz\), Ox và Oz cắt nhau tại O và nằm trong mặt phẳng (Oxz) nên \(Oy \bot \left( {Oxz} \right)\). Mà \(Oy \subset \left( {Oxy} \right) \Rightarrow \left( {Oxz} \right) \bot \left( {Oxy} \right),Oy \subset \left( {Oyz} \right) \Rightarrow \left( {Oyz} \right) \bot \left( {Oxz} \right)\)
Chứng minh tương tự ta có: \(\left( {Oyz} \right) \bot \left( {Oxy} \right)\)
Vậy ba mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau.
LT1
Trả lời câu hỏi Luyện tập 1 trang 61SGK Toán 12 Kết nối tri thức
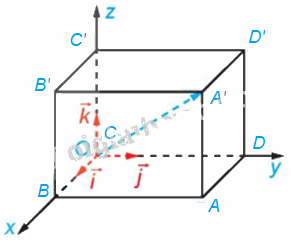
Cho hình hộp chữ nhật ABCD.A’B’C’D’. Có thể lập một hệ tọa độ Oxyz có gốc O trùng với đỉnh C và các vectơ \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) lần lượt cùng hướng với các vectơ \(\overrightarrow {CB} ,\overrightarrow {CD} ,\overrightarrow {CC'} \) không? Vì sao?
Phương pháp giải:
Sử dụng kiến thức về hệ tọa độ trong không gian để mô tả: Trong không gian, ba trục Ox, Oy, Oz đôi một vuông góc với nhau tại gốc O của mỗi trục. Gọi \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) lần lượt là các vectơ đơn vị trên các trục Ox, Oy, Oz. Hệ ba trục tọa độ như vậy được gọi là hệ trục tọa độ Descartes vuông góc Oxyz (hay đơn giản là hệ tọa độ Oxyz). Điểm O được gọi là gốc tọa độ, các mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau và được gọi là các mặt phẳng tọa độ. Không gian với hệ tọa độ Oxyz còn được gọi là không gian Oxyz.
Lời giải chi tiết:
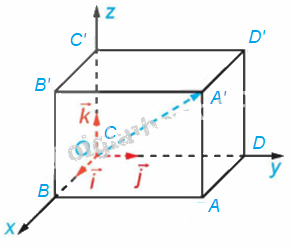
Vì ABCD. A’B’C’D’ là hình hộp chữ nhật nên các cạnh CC’, CB và CD đôi một vuông góc với nhau.
Các vectơ \(\overrightarrow {CB} ,\overrightarrow {CD} ,\overrightarrow {CC'} \) cùng có điểm đầu là C.
Do đó, suy ra có thể lập một hệ tọa độ Oxyz có gốc O trùng với đỉnh C và các vectơ \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) lần lượt cùng hướng với các vectơ \(\overrightarrow {CB} ,\overrightarrow {CD} ,\overrightarrow {CC'} \).
CH
Trả lời Câu hỏi trang 61 SGK Toán 12 Kết nối tri thức
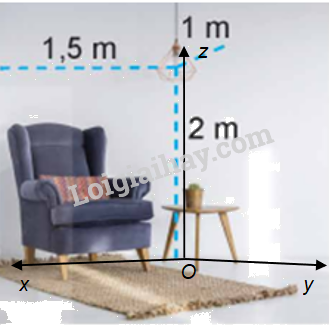
Góc căn phòng trong Hình 2.34 có gợi lên hình ảnh về hệ tọa độ Oxyz trong không gian hay không? Nếu có hãy mô tả gốc tọa độ và các mặt phẳng tọa độ trong hình ảnh đó.

Phương pháp giải:
Sử dụng kiến thức hệ về hệ tọa độ trong không gian để mô tả: Trong không gian, ba trục Ox, Oy, Oz đôi một vuông góc với nhau tại gốc O của mỗi trục. Hệ ba trục tọa độ như vậy được gọi là hệ trục tọa độ Descartes vuông góc Oxyz (hay đơn giản là hệ tọa độ Oxyz). Điểm O được gọi là gốc tọa độ, các mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau và được gọi là các mặt phẳng tọa độ. Không gian với hệ tọa độ Oxyz còn được gọi là không gian Oxyz.
Lời giải chi tiết:
Góc căn phòng trong Hình 2.34 gợi lên hình ảnh về hệ trục tọa độ Oxyz trong không gian.
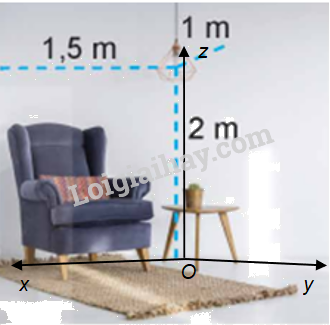
Mô tả: Hệ tọa độ Oxyz có:
+ Mặt phẳng (Oxy) là sàn nhà, hai mặt phẳng (Oyz), (Ozx) hai bức tường. Khi đó, ba mặt phẳng đôi một vuông góc với nhau.
+ Gốc tọa độ O (trùng với một góc phòng) là giao điểm của ba trục Ox, Oy, Oz.
- HĐ1
- CH
- LT1
Trả lời câu hỏi Hoạt động 1 trang 60 SGK Toán 12 Kết nối tri thức
Trong không gian, xét ba trục Ox, Oy, Oz có chung gốc O và đôi một vuông góc với nhau. Gọi \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) là các vectơ đơn vị trên các trục đó (H.2.35).
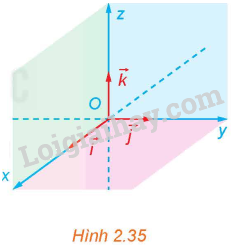
a) Gọi tên các mặt phẳng tọa độ có trong Hình 2.35.
b) Các mặt phẳng tọa độ trong Hình 2.35 có đôi một vuông góc với nhau không?
Phương pháp giải:
Sử dụng kiến thức về hai mặt phẳng vuông góc để chứng minh: Nếu mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia thì hai mặt phẳng đó vuông góc với nhau.
Lời giải chi tiết:
a) Các mặt phẳng có trong hình vẽ là: Mặt phẳng (Oxy), (Oyz), (Ozx).
b) Vì \(Ox \bot Oy,Oy \bot Oz\), Ox và Oz cắt nhau tại O và nằm trong mặt phẳng (Oxz) nên \(Oy \bot \left( {Oxz} \right)\). Mà \(Oy \subset \left( {Oxy} \right) \Rightarrow \left( {Oxz} \right) \bot \left( {Oxy} \right),Oy \subset \left( {Oyz} \right) \Rightarrow \left( {Oyz} \right) \bot \left( {Oxz} \right)\)
Chứng minh tương tự ta có: \(\left( {Oyz} \right) \bot \left( {Oxy} \right)\)
Vậy ba mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau.
Trả lời Câu hỏi trang 61 SGK Toán 12 Kết nối tri thức
Góc căn phòng trong Hình 2.34 có gợi lên hình ảnh về hệ tọa độ Oxyz trong không gian hay không? Nếu có hãy mô tả gốc tọa độ và các mặt phẳng tọa độ trong hình ảnh đó.

Phương pháp giải:
Sử dụng kiến thức hệ về hệ tọa độ trong không gian để mô tả: Trong không gian, ba trục Ox, Oy, Oz đôi một vuông góc với nhau tại gốc O của mỗi trục. Hệ ba trục tọa độ như vậy được gọi là hệ trục tọa độ Descartes vuông góc Oxyz (hay đơn giản là hệ tọa độ Oxyz). Điểm O được gọi là gốc tọa độ, các mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau và được gọi là các mặt phẳng tọa độ. Không gian với hệ tọa độ Oxyz còn được gọi là không gian Oxyz.
Lời giải chi tiết:
Góc căn phòng trong Hình 2.34 gợi lên hình ảnh về hệ trục tọa độ Oxyz trong không gian.
Mô tả: Hệ tọa độ Oxyz có:
+ Mặt phẳng (Oxy) là sàn nhà, hai mặt phẳng (Oyz), (Ozx) hai bức tường. Khi đó, ba mặt phẳng đôi một vuông góc với nhau.
+ Gốc tọa độ O (trùng với một góc phòng) là giao điểm của ba trục Ox, Oy, Oz.
Trả lời câu hỏi Luyện tập 1 trang 61SGK Toán 12 Kết nối tri thức
Cho hình hộp chữ nhật ABCD.A’B’C’D’. Có thể lập một hệ tọa độ Oxyz có gốc O trùng với đỉnh C và các vectơ \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) lần lượt cùng hướng với các vectơ \(\overrightarrow {CB} ,\overrightarrow {CD} ,\overrightarrow {CC'} \) không? Vì sao?
Phương pháp giải:
Sử dụng kiến thức về hệ tọa độ trong không gian để mô tả: Trong không gian, ba trục Ox, Oy, Oz đôi một vuông góc với nhau tại gốc O của mỗi trục. Gọi \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) lần lượt là các vectơ đơn vị trên các trục Ox, Oy, Oz. Hệ ba trục tọa độ như vậy được gọi là hệ trục tọa độ Descartes vuông góc Oxyz (hay đơn giản là hệ tọa độ Oxyz). Điểm O được gọi là gốc tọa độ, các mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau và được gọi là các mặt phẳng tọa độ. Không gian với hệ tọa độ Oxyz còn được gọi là không gian Oxyz.
Lời giải chi tiết:
Vì ABCD. A’B’C’D’ là hình hộp chữ nhật nên các cạnh CC’, CB và CD đôi một vuông góc với nhau.
Các vectơ \(\overrightarrow {CB} ,\overrightarrow {CD} ,\overrightarrow {CC'} \) cùng có điểm đầu là C.
Do đó, suy ra có thể lập một hệ tọa độ Oxyz có gốc O trùng với đỉnh C và các vectơ \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) lần lượt cùng hướng với các vectơ \(\overrightarrow {CB} ,\overrightarrow {CD} ,\overrightarrow {CC'} \).
Giải mục 1 trang 60, 61 SGK Toán 12 tập 1 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 1 trang 60, 61 SGK Toán 12 tập 1 - Kết nối tri thức tập trung vào việc ôn tập về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Đây là một phần kiến thức nền tảng quan trọng, xuất hiện thường xuyên trong các bài thi THPT Quốc gia. Việc nắm vững kiến thức và kỹ năng giải bài tập trong mục này sẽ giúp học sinh đạt kết quả tốt hơn.
Nội dung chính của Mục 1
- Ôn tập khái niệm đạo hàm: Định nghĩa đạo hàm, quy tắc tính đạo hàm của các hàm số cơ bản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit).
- Ứng dụng đạo hàm để khảo sát hàm số: Tìm cực trị, điểm uốn, khoảng đồng biến, nghịch biến của hàm số.
- Bài tập vận dụng: Giải các bài tập liên quan đến việc tính đạo hàm, khảo sát hàm số và ứng dụng đạo hàm vào các bài toán thực tế.
Phương pháp giải bài tập hiệu quả
- Nắm vững lý thuyết: Hiểu rõ các định nghĩa, quy tắc và công thức liên quan đến đạo hàm và ứng dụng của đạo hàm.
- Phân tích đề bài: Xác định rõ yêu cầu của đề bài, các dữ kiện đã cho và các kiến thức cần sử dụng.
- Sử dụng các công cụ hỗ trợ: Máy tính bỏ túi, phần mềm vẽ đồ thị hàm số có thể giúp kiểm tra lại kết quả và hiểu rõ hơn về hàm số.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập thường gặp.
Giải chi tiết các bài tập trong Mục 1
Dưới đây là lời giải chi tiết cho các bài tập trong Mục 1 trang 60, 61 SGK Toán 12 tập 1 - Kết nối tri thức:
Bài 1: Tính đạo hàm của các hàm số sau
a) y = x3 - 2x2 + 5x - 1
Lời giải: y' = 3x2 - 4x + 5
b) y = sin(2x) + cos(x)
Lời giải: y' = 2cos(2x) - sin(x)
Bài 2: Tìm cực trị của hàm số y = x3 - 3x2 + 2
Lời giải:
- Tính đạo hàm: y' = 3x2 - 6x
- Tìm điểm dừng: y' = 0 => x = 0 hoặc x = 2
- Khảo sát dấu của y':
- Khi x < 0: y' > 0 => Hàm số đồng biến
- Khi 0 < x < 2: y' < 0 => Hàm số nghịch biến
- Khi x > 2: y' > 0 => Hàm số đồng biến
- Kết luận: Hàm số đạt cực đại tại x = 0, ymax = 2 và đạt cực tiểu tại x = 2, ymin = -2
Bài 3: Tìm khoảng đồng biến, nghịch biến của hàm số y = x4 - 4x2 + 3
Lời giải:
- Tính đạo hàm: y' = 4x3 - 8x
- Tìm điểm dừng: y' = 0 => x = 0, x = √2, x = -√2
- Khảo sát dấu của y': (Tương tự như bài 2)
- Kết luận: Hàm số đồng biến trên các khoảng (-∞, -√2) và (√2, +∞), nghịch biến trên khoảng (-√2, 0) và (0, √2).
Lưu ý khi giải bài tập
Trong quá trình giải bài tập, các em cần chú ý:
- Kiểm tra kỹ các điều kiện của bài toán.
- Sử dụng đúng các công thức và quy tắc.
- Biết cách trình bày lời giải một cách rõ ràng, logic.
Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả này, các em sẽ tự tin hơn khi giải các bài tập trong Mục 1 trang 60, 61 SGK Toán 12 tập 1 - Kết nối tri thức. Chúc các em học tốt!