Giải mục 3 trang 23, 24 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 3 trang 23, 24 SGK Toán 12 tập 1 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 23, 24 sách giáo khoa Toán 12 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em hiểu rõ các khái niệm, định lý và phương pháp giải bài tập liên quan đến chủ đề này.
tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp tài liệu học tập chất lượng và lời giải chính xác, dễ hiểu.
Đường tiệm cận xiên
LT3
Trả lời câu hỏi Luyện tập 3 trang 24 SGK Toán 12 Kết nối tri thức
Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - 4x + 2}}{{1 - x}}\).
Phương pháp giải:
Sử dụng kiến thức về tìm khái niệm đường tiệm cận xiên để tìm tiệm cận xiên: Đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\).
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 4x + 2}}{{1 - x}} = + \infty \); \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} - 4x + 2}}{{1 - x}} = - \infty \)
Vậy tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\) là đường thẳng \(x = 1\)
Ta có: \(y = f\left( x \right) = \frac{{{x^2} - 4x + 2}}{{1 - x}} = - x + 3 - \frac{1}{{1 - x}}\)
Do đó, \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( { - x + 3} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 1}}{{1 - x}} = 0\), \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( { - x + 3} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - 1}}{{1 - x}} = 0\)
Vậy tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right)\) là đường thẳng \(y = - x + 3\)
- HĐ3
- LT3
Trả lời câu hỏi Hoạt động 3 trang 23 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f\left( x \right) = x - 1 + \frac{2}{{x + 1}}\) có đồ thị (C) và đường thẳng \(y = x - 1\) như Hình 1.24.
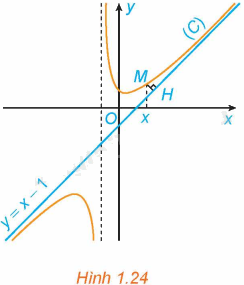
a) Với \(x > - 1\), xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng \(y = x - 1\). Có nhận xét gì về khoảng cách MH khi \(x \to + \infty \)?
b) Chứng tỏ rằng \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x - 1} \right)} \right] = 0\). Tính chất này thể hiện trên Hình 1.24 như thế nào?
Phương pháp giải:
Sử dụng kiến thức về giới hạn của hàm số để tính giới hạn.
Lời giải chi tiết:
a) Nhìn vào đồ thị ta thấy, khi \(x \to + \infty \) thì khoảng cách MH tiến tới 0.
b) Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left[ {x - 1 + \frac{2}{{x + 1}} - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{2}{{x + 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{2}{x}}}{{1 + \frac{1}{x}}} = 0\)
Tính chất này được thể hiện trong Hình 1.24 là: Khoảng cách từ điểm M của đồ thị hàm số (C) đến đường thẳng \(y = x - 1\) tiến đến 0 khi \(x \to + \infty \).
Trả lời câu hỏi Luyện tập 3 trang 24 SGK Toán 12 Kết nối tri thức
Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - 4x + 2}}{{1 - x}}\).
Phương pháp giải:
Sử dụng kiến thức về tìm khái niệm đường tiệm cận xiên để tìm tiệm cận xiên: Đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\).
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 4x + 2}}{{1 - x}} = + \infty \); \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} - 4x + 2}}{{1 - x}} = - \infty \)
Vậy tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\) là đường thẳng \(x = 1\)
Ta có: \(y = f\left( x \right) = \frac{{{x^2} - 4x + 2}}{{1 - x}} = - x + 3 - \frac{1}{{1 - x}}\)
Do đó, \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( { - x + 3} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 1}}{{1 - x}} = 0\), \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( { - x + 3} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - 1}}{{1 - x}} = 0\)
Vậy tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right)\) là đường thẳng \(y = - x + 3\)
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 23 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f\left( x \right) = x - 1 + \frac{2}{{x + 1}}\) có đồ thị (C) và đường thẳng \(y = x - 1\) như Hình 1.24.
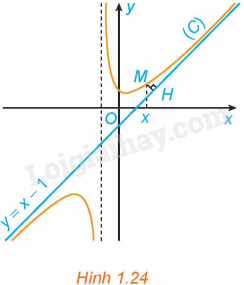
a) Với \(x > - 1\), xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng \(y = x - 1\). Có nhận xét gì về khoảng cách MH khi \(x \to + \infty \)?
b) Chứng tỏ rằng \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x - 1} \right)} \right] = 0\). Tính chất này thể hiện trên Hình 1.24 như thế nào?
Phương pháp giải:
Sử dụng kiến thức về giới hạn của hàm số để tính giới hạn.
Lời giải chi tiết:
a) Nhìn vào đồ thị ta thấy, khi \(x \to + \infty \) thì khoảng cách MH tiến tới 0.
b) Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left[ {x - 1 + \frac{2}{{x + 1}} - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{2}{{x + 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{2}{x}}}{{1 + \frac{1}{x}}} = 0\)
Tính chất này được thể hiện trong Hình 1.24 là: Khoảng cách từ điểm M của đồ thị hàm số (C) đến đường thẳng \(y = x - 1\) tiến đến 0 khi \(x \to + \infty \).
Giải mục 3 trang 23, 24 SGK Toán 12 tập 1 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 3 trang 23, 24 SGK Toán 12 tập 1 Kết nối tri thức tập trung vào việc ôn tập chương 1: Hàm số và đồ thị. Đây là một chương quan trọng, đặt nền móng cho các kiến thức toán học bậc cao hơn. Việc nắm vững kiến thức trong chương này là vô cùng cần thiết để các em có thể giải quyết các bài toán phức tạp trong các chương tiếp theo.
Nội dung chính của Mục 3
Mục 3 bao gồm các bài tập tổng hợp, giúp học sinh củng cố kiến thức về:
- Hàm số bậc hai: Xác định hàm số, tìm tập xác định, tập giá trị, đỉnh, trục đối xứng, giao điểm với các trục tọa độ.
- Đồ thị hàm số bậc hai: Vẽ đồ thị hàm số, xác định các yếu tố quan trọng của đồ thị.
- Bất phương trình bậc hai: Giải bất phương trình bậc hai, biểu diễn nghiệm trên trục số.
- Ứng dụng của hàm số bậc hai: Giải các bài toán thực tế liên quan đến hàm số bậc hai.
Hướng dẫn giải chi tiết các bài tập
Bài 1: Tìm tập xác định của hàm số
Để tìm tập xác định của hàm số, ta cần xác định các giá trị của x sao cho biểu thức trong hàm số có nghĩa. Ví dụ, nếu hàm số có chứa căn bậc hai, ta cần đảm bảo biểu thức dưới dấu căn lớn hơn hoặc bằng 0. Nếu hàm số có chứa phân số, ta cần đảm bảo mẫu số khác 0.
Bài 2: Xác định đỉnh và trục đối xứng của parabol
Đỉnh của parabol có tọa độ (x0, y0), trong đó x0 = -b/2a và y0 = f(x0). Trục đối xứng của parabol là đường thẳng x = x0.
Bài 3: Giải bất phương trình bậc hai
Để giải bất phương trình bậc hai, ta có thể sử dụng phương pháp xét dấu hoặc phương pháp vẽ đồ thị. Phương pháp xét dấu dựa trên việc xác định khoảng nghiệm của bất phương trình. Phương pháp vẽ đồ thị dựa trên việc xác định vị trí của đồ thị hàm số so với trục hoành.
Mẹo giải nhanh
Để giải nhanh các bài tập trong mục 3, các em có thể áp dụng các mẹo sau:
- Sử dụng công thức: Nắm vững các công thức liên quan đến hàm số bậc hai, đồ thị hàm số và bất phương trình bậc hai.
- Phân tích bài toán: Đọc kỹ đề bài, xác định các yếu tố quan trọng và lựa chọn phương pháp giải phù hợp.
- Kiểm tra lại kết quả: Sau khi giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Ví dụ minh họa
Bài tập: Giải bất phương trình x2 - 5x + 6 > 0
Lời giải:
- Tìm nghiệm của phương trình x2 - 5x + 6 = 0. Ta có x1 = 2 và x2 = 3.
- Vẽ đồ thị hàm số y = x2 - 5x + 6.
- Xác định khoảng nghiệm của bất phương trình. Vì hệ số a = 1 > 0, đồ thị hàm số hướng lên trên. Do đó, bất phương trình có nghiệm khi x < 2 hoặc x > 3.
Tổng kết
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em đã nắm vững kiến thức và phương pháp giải các bài tập trong mục 3 trang 23, 24 SGK Toán 12 tập 1 Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ.