Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài tập 6.18 trang 79 SGK Toán 12 tập 2 - Kết nối tri thức
SGK Toán 12 - Kết nối tri thức
Giải Toán 12 tập 2 - Kết nối tri thức
Chương 6. Xác suất có điều kiện
Bài tập cuối chương 6

Giải bài tập 6.18 trang 79 SGK Toán 12 tập 2 - Kết nối tri thức

Giải Bài Tập 6.18 Trang 79 Toán 12 Tập 2 - Kết Nối Tri Thức

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 6.18 trang 79 SGK Toán 12 tập 2 - Kết nối tri thức. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, phương pháp giải dễ hiểu và nhanh chóng.

Để thử nghiệm tác dụng điều trị bệnh mất ngủ của hai loại thuốc X và thuốc Y, người ta tiến hành thử nghiệm với 4 000 người bệnh tình nguyện. Kết quả được cho trong bảng dữ liệu thống kê \(2 \times 2\) sau: Chọn ngẫu nhiên một người bệnh tham gia tình nguyện thử nghiệm thuốc. a) Tính xác suất để người đó khỏi bệnh nếu biết người đó uống thuốc X. b) Tính xác suất để người bệnh đó uống thuốc Y, biết rằng người đó khỏi bệnh.

Đề bài

Để thử nghiệm tác dụng điều trị bệnh mất ngủ của hai loại thuốc X và thuốc Y, người ta tiến hành thử nghiệm với 4 000 người bệnh tình nguyện. Kết quả được cho trong bảng dữ liệu thống kê \(2 \times 2\) sau:

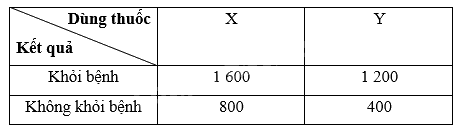
Giải bài tập 6.18 trang 79 SGK Toán 12 tập 2 - Kết nối tri thức 1

Chọn ngẫu nhiên một người bệnh tham gia tình nguyện thử nghiệm thuốc.

a) Tính xác suất để người đó khỏi bệnh nếu biết người đó uống thuốc X.

b) Tính xác suất để người bệnh đó uống thuốc Y, biết rằng người đó khỏi bệnh.

Phương pháp giải - Xem chi tiếtGiải bài tập 6.18 trang 79 SGK Toán 12 tập 2 - Kết nối tri thức 2

Sử dụng kiến thức về công thức tính xác suất có điều kiện để tính: Cho hai biến cố A và B bất kì, với \(P\left( B \right) > 0\). Khi đó, \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}}\)

Lời giải chi tiết

Không gian mẫu \(\Omega \) là tập hợp gồm 4 000 bệnh nhân thử nghiệm nên \(n\left( \Omega \right) = 4000\)

a) Gọi A là biến cố: “Người đó uống thuốc X”, B là biến cố “Người đó khỏi bệnh”.

Khi đó biến cố AB là: “Người đó uống thuốc X và khỏi bệnh”

Ta có: \(1600 + 800 = 2400\) người uống thuốc X nên \(n\left( A \right) = 2400\). Do đó, \(P\left( A \right) = \frac{{2400}}{{4000}}\)

Trong số những người uống thuốc X, có 1 600 người khỏi bệnh nên \(n\left( {AB} \right) = 1\;600\)

Do đó, \(P\left( {AB} \right) = \frac{{1600}}{{4000}}\). Vậy \(P\left( {B|A} \right) = \frac{{P\left( {AB} \right)}}{{P\left( A \right)}} = \frac{{1600}}{{2400}} = \frac{2}{3}\)

b) Gọi A là biến cố: “Người đó uống thuốc Y”, B là biến cố “Người đó khỏi bệnh”

Khi đó biến cố AB là: “Người đó uống thuốc Y và khỏi bệnh”.

Ta có: \(1200 + 1600 = 2800\) khỏi bệnh nên \(n\left( B \right) = 2800\). Do đó, \(P\left( B \right) = \frac{{2800}}{{4000}}\)

Trong số những người khỏi bệnh, có 1200 người uống thuốc Y nên \(n\left( {AB} \right) = 1200\)

Do đó, \(P\left( {AB} \right) = \frac{{1200}}{{2800}}\). Vậy \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{1200}}{{2800}} = \frac{3}{7}\)

Giải Bài Tập 6.18 Trang 79 Toán 12 Tập 2 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết

Bài tập 6.18 trang 79 SGK Toán 12 tập 2 - Kết nối tri thức yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức về đạo hàm, điều kiện cực trị và cách xác định khoảng đồng biến, nghịch biến của hàm số.

Đề Bài:

Cho hàm số y = x3 - 3x2 + 2. Hãy khảo sát hàm số và tìm các điểm cực trị.

Lời Giải:

  1. Xác định tập xác định: Hàm số y = x3 - 3x2 + 2 có tập xác định là D = ℝ.
  2. Tính đạo hàm cấp nhất: y' = 3x2 - 6x.
  3. Tìm điểm dừng: Giải phương trình y' = 0, ta được 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0. Vậy x = 0 hoặc x = 2.
  4. Lập bảng xét dấu y':
    x-∞02+∞
    y'+-+
    yNBĐBNB

    (NB: Đồng biến, ĐB: Nghịch biến)

  5. Kết luận:
    • Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞).
    • Hàm số nghịch biến trên khoảng (0; 2).
    • Hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2.
    • Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.

Lưu Ý Quan Trọng:

Khi giải các bài tập về khảo sát hàm số, điều quan trọng là phải nắm vững các bước thực hiện và áp dụng đúng các công thức, định lý. Ngoài ra, việc vẽ đồ thị hàm số cũng giúp chúng ta hiểu rõ hơn về tính chất của hàm số.

Mở Rộng:

Để hiểu sâu hơn về ứng dụng của đạo hàm trong việc khảo sát hàm số, các em có thể tham khảo thêm các bài tập tương tự trong SGK và sách bài tập Toán 12 tập 2 - Kết nối tri thức. Tusach.vn sẽ tiếp tục cập nhật và cung cấp các lời giải chi tiết cho các bài tập khác.

Tổng Kết:

Bài tập 6.18 trang 79 SGK Toán 12 tập 2 - Kết nối tri thức là một bài tập điển hình về khảo sát hàm số và tìm các điểm cực trị. Hy vọng với lời giải chi tiết này, các em học sinh có thể hiểu rõ hơn về phương pháp giải và áp dụng vào các bài tập tương tự.

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN