Giải bài tập 1.16 trang 25 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 1.16 Trang 25 Toán 12 Tập 1 - Kết Nối Tri Thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 12 tập 1 - Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn giải bài tập 1.16 trang 25 một cách dễ hiểu nhất.
Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Hình 1.26 là đồ thị của hàm số (y = fleft( x right) = frac{{2{x^2}}}{{{x^2} - 1}}) Sử dụng đồ thị này, hãy: a) Viết kết quả của các giới hạn sau: (mathop {lim }limits_{x to - infty } fleft( x right)); (mathop {lim }limits_{x to + infty } fleft( x right)); (mathop {lim }limits_{x to {1^ - }} fleft( x right)); (mathop {lim }limits_{x to - {1^ + }} fleft( x right)) b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.
Đề bài
Hình 1.26 là đồ thị của hàm số \(y = f\left( x \right) = \frac{{2{x^2}}}{{{x^2} - 1}}\)
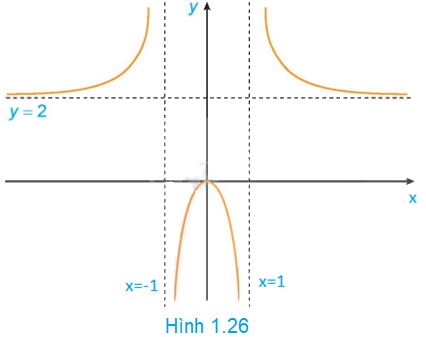
Sử dụng đồ thị này, hãy:a) Viết kết quả của các giới hạn sau: \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)\); \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\); \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right)\); \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right)\)b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\)
Sử dụng kiến thức về khái niệm tiệm cận đứng của đồ thị hàm số để tìm tiệm cận đứng: Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số \(y = f\left( x \right)\) nếu ít nhất một trong các điều kiện sau được thỏa mãn: \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty \)
Lời giải chi tiết
a) \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2\); \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\); \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = - \infty \)
b) Do đó, tiệm cận đứng của đồ thị hàm số là \(x = 1;x = - 1\).
Tiệm cận ngang của đồ thị hàm số là \(y = 2\)
Giải Bài Tập 1.16 Trang 25 Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 1.16 trang 25 SGK Toán 12 tập 1 Kết nối tri thức thuộc chương 1: Hàm số và đồ thị. Bài tập này thường liên quan đến việc xác định tính đơn điệu của hàm số, tìm khoảng đồng biến, nghịch biến và cực trị của hàm số. Để giải bài tập này một cách hiệu quả, bạn cần nắm vững các kiến thức cơ bản về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
I. Đề Bài Bài Tập 1.16 Trang 25 Toán 12 Tập 1 - Kết Nối Tri Thức
(Đề bài cụ thể của bài tập 1.16 sẽ được chèn vào đây. Ví dụ: Cho hàm số y = f(x) = x3 - 3x2 + 2. Hãy tìm khoảng đồng biến, nghịch biến và cực trị của hàm số.)
II. Phương Pháp Giải Bài Tập Khảo Sát Hàm Số
Để giải bài tập khảo sát hàm số, bạn có thể thực hiện theo các bước sau:
- Xác định tập xác định của hàm số.
- Tính đạo hàm cấp nhất f'(x).
- Tìm các điểm tới hạn (điểm mà f'(x) = 0 hoặc f'(x) không xác định).
- Lập bảng biến thiên của hàm số.
- Kết luận về khoảng đồng biến, nghịch biến, cực đại, cực tiểu của hàm số.
III. Lời Giải Chi Tiết Bài Tập 1.16 Trang 25 Toán 12 Tập 1 - Kết Nối Tri Thức
(Lời giải chi tiết của bài tập 1.16 sẽ được trình bày ở đây, bao gồm các bước tính toán, lập luận và kết luận. Ví dụ:)
Bước 1: Tập xác định của hàm số y = f(x) = x3 - 3x2 + 2 là R.
Bước 2: Đạo hàm cấp nhất của hàm số là f'(x) = 3x2 - 6x.
Bước 3: Giải phương trình f'(x) = 0, ta được 3x2 - 6x = 0 => x(x - 2) = 0 => x = 0 hoặc x = 2.
Bước 4: Lập bảng biến thiên:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | NB | ĐB | NB |
Bước 5: Kết luận: Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2). Hàm số đạt cực đại tại x = 0 với giá trị f(0) = 2 và đạt cực tiểu tại x = 2 với giá trị f(2) = -2.
IV. Bài Tập Tương Tự
- Bài tập 1.17 trang 25 SGK Toán 12 tập 1 Kết nối tri thức
- Bài tập 1.18 trang 25 SGK Toán 12 tập 1 Kết nối tri thức
V. Lời Khuyên Khi Giải Bài Tập Khảo Sát Hàm Số
Để giải bài tập khảo sát hàm số một cách hiệu quả, bạn nên:
- Nắm vững các kiến thức cơ bản về đạo hàm và ứng dụng của đạo hàm.
- Thực hành giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng.
- Sử dụng máy tính cầm tay để hỗ trợ tính toán và vẽ đồ thị hàm số.
- Kiểm tra lại kết quả sau khi giải bài tập để đảm bảo tính chính xác.
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài tập 1.16 trang 25 SGK Toán 12 tập 1 Kết nối tri thức. Chúc bạn học tập tốt!