Giải mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 chương trình Kết nối tri thức. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài học, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong các kỳ thi.
Cực trị của hàm số
VD2
Trả lời câu hỏi Vận dụng 2 trang 12 SGK Toán 12 Kết nối tri thức
Một vật được phóng thẳng đứng lên trên từ độ cao 2m với vận tốc ban đầu là 24,5m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h (mét) của vật sau t (giây) được cho bởi công thức: \(h\left( t \right) = 2 + 24,5t - 4,9{t^2}\). Hỏi tại thời điểm nào thì vật đạt độ cao lớn nhất?
Phương pháp giải:
Sử dụng kiến thức về cách tìm cực trị của hàm số \(y = f\left( x \right)\) để tìm thời điểm vật đạt độ cao lớn nhất:
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.
Lời giải chi tiết:
Xét hàm số: \(h\left( t \right) = 2 + 24,5t - 4,9{t^2}\).
Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \[h'\left( t \right) = - 9,8t + 24,5;h'\left( t \right) = 0 \Leftrightarrow - 9,8t + 24,5 = 0 \Leftrightarrow t = \frac{5}{2}\].
Bảng biến thiên:
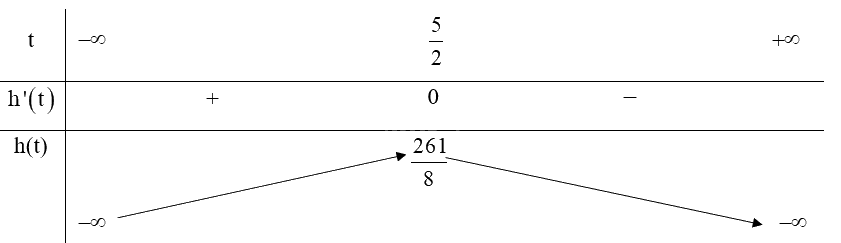
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại \(t = \frac{5}{2}\),
Vậy thời điểm vật đạt độ cao lớn nhất là \(t = \frac{5}{2}\) giây
HĐ5
Trả lời câu hỏi Hoạt động 5 trang 10 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 8x + 1\).
a) Tính đạo hàm \(f'\left( x \right)\) và tìm các điểm mà tại đó đạo hàm \(f'\left( x \right)\) bằng 0.
b) Lập bảng biến thiên của hàm số.
c) Từ bảng biến thiên suy ra các điểm cực trị của hàm số.
Phương pháp giải:
Sử dụng kiến thức về định nghĩa cực đại, cực tiểu của hàm số để tìm cực đại, cực tiểu của hàm số: Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên khoảng (a; b) (a có thể là \( - \infty \), b có thể là \( + \infty \)) và điểm \({x_0} \in \left( {a;b} \right)\).
+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) < f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực đại tại \({x_0}\).
+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) > f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực tiểu tại \({x_0}\).
Lời giải chi tiết:
a) Tập xác định: \(D = \mathbb{R}\).
\(y' = {x^2} - 6x + 8\), \(y' = 0 \Leftrightarrow {x^2} - 6x + 8 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = 2\end{array} \right.\)
Vậy \(x = 4;x = 2\) thì \(f'\left( x \right) = 0\)
b) Bảng biến thiên:
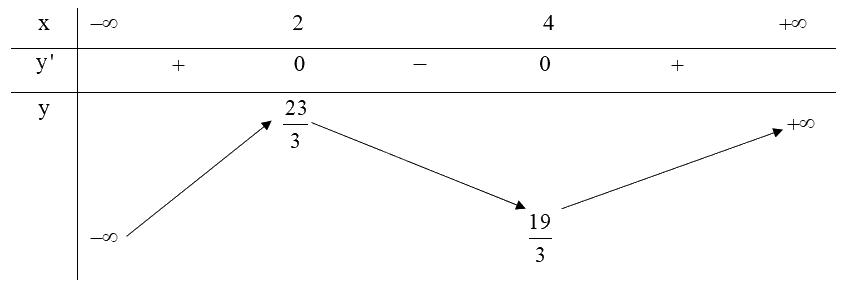
c) Từ bảng biến thiên ta có:
Hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 8x + 1\) có điểm cực đại là \(\left( {2;\frac{{23}}{3}} \right)\).
Hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 8x + 1\) có điểm cực tiểu là \(\left( {4;\frac{{19}}{3}} \right)\).
LT5
Trả lời câu hỏi Luyện tập 5 trang 12 SGK Toán 12 Kết nối tri thức
Tìm cực trị của các hàm số sau:
a) \(y = {x^4} - 3{x^2} + 1\);
b) \(y = \frac{{ - {x^2} + 2x - 1}}{{x + 2}}\).
Phương pháp giải:
Sử dụng kiến thức về cách tìm cực trị của hàm số \(y = f\left( x \right)\) để tìm cực trị của hàm số:
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.
Lời giải chi tiết:
a) Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \(y' = 4{x^3} - 6x,y' = 0 \Leftrightarrow 4{x^3} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \frac{{\sqrt 6 }}{2}\end{array} \right.\);
Bảng biến thiên:
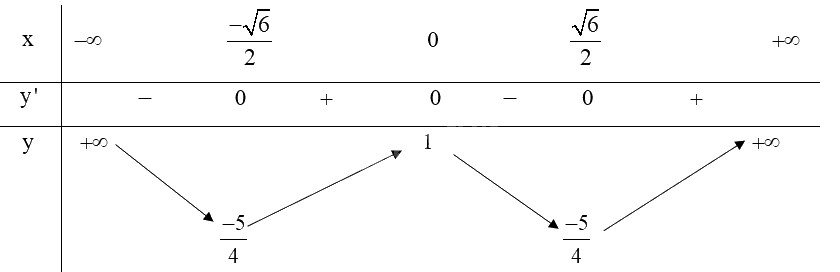
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại \(x = 0\) và .
Hàm số đạt cực tiểu tại \(x = \pm \frac{{\sqrt 6 }}{2}\) và \({y_{CT}} = \frac{{ - 5}}{4}\).
b) Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Ta có: \(y' = \frac{{\left( { - 2x + 2} \right)\left( {x + 2} \right) - \left( { - {x^2} + 2x - 1} \right)}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{ - {x^2} - 4x + 5}}{{{{\left( {x + 2} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 5\\x = 1\end{array} \right.\) (thỏa mãn)
Lập bảng biến thiên của hàm số:
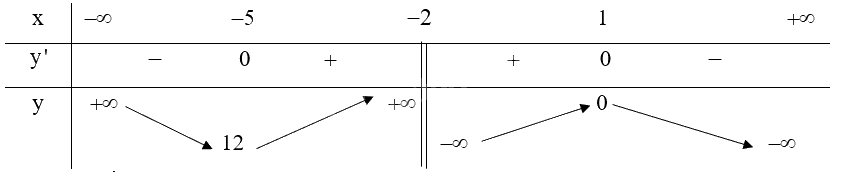
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại \(x = 1\) và .
Hàm số đạt cực tiểu tại \(x = - 5\) và \({y_{CT}} = 12\).
CH
Trả lời câu hỏi trang 11 SGK Toán 12 Kết nối tri thức
Giải thích vì sao nếu f’(x) không đổi dấu qua \({x_0}\) thì \({x_0}\) không phải là điểm cực trị của hàm số f(x)?
Phương pháp giải:
Sử dụng kiến thức về định lí cực trị hàm số để chứng minh: Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Khi đó:
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực tiểu của hàm số f(x).
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực đại của hàm số f(x).d
Lời giải chi tiết:
Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Nếu f’(x) không đổi dấu qua \({x_0}\) thì:
TH1: \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\), ta có bảng biến thiên:
Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Nếu f’(x) không đổi dấu qua \({x_0}\) thì:
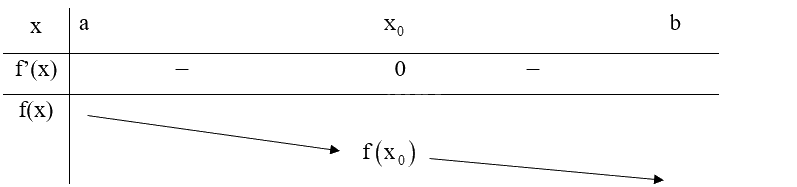
TH1: \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\), ta có bảng biến thiên:
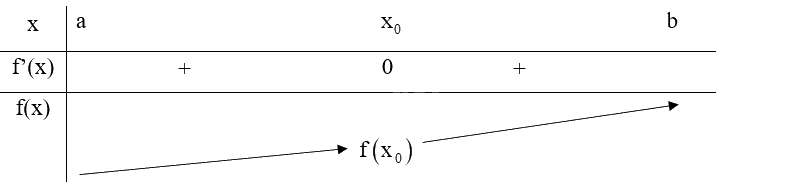
Do đó, \({x_0}\) không phải là điểm cực trị của hàm số f(x).
LT4
Trả lời câu hỏi Luyện tập 4 trang 10 SGK Toán 12 Kết nối tri thức
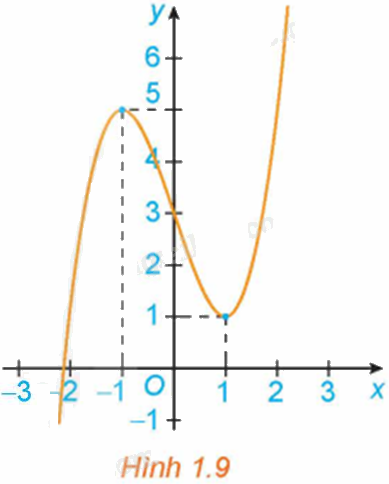
Hình 1.9 là đồ thị của hàm số \(y = f\left( x \right)\). Hãy tìm các cực trị của hàm số.
Phương pháp giải:
Sử dụng kiến thức về định nghĩa cực đại, cực tiểu của hàm số để tìm cực đại, cực tiểu của hàm số: Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên khoảng (a; b) (a có thể là \( - \infty \), b có thể là \( + \infty \)) và điểm \({x_0} \in \left( {a;b} \right)\).
+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) < f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực đại tại \({x_0}\).
+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) > f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực tiểu tại \({x_0}\).
Lời giải chi tiết:
Từ đồ thị hàm số, ta có:
Hàm số đạt cực tiểu tại \(x = 1\) và \({y_{CT}} = y\left( 1 \right) = 1\).
Hàm số đạt cực đại tại \(x = - 1\) và \({y_{C{\rm{D}}}} = y( - 1) = 5\)
HĐ4
Trả lời câu hỏi Hoạt động 4 trang 9 SGK Toán 12 Kết nối tri thức
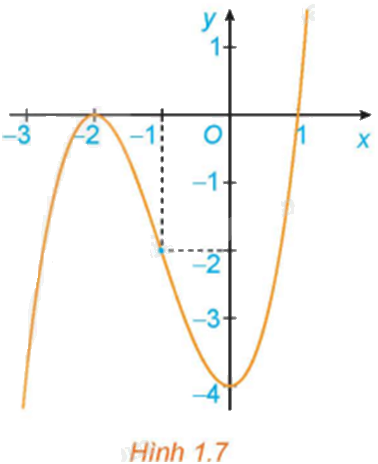
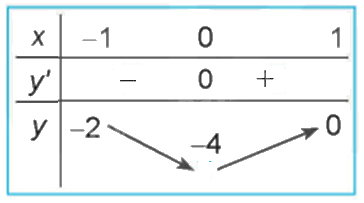
Quan sát đồ thị của hàm số \(y = {x^3} + 3{x^2} - 4\) (H.1.7). Xét dấu đạo hàm của hàm số đã cho và hoàn thành các bảng sau vào vở:
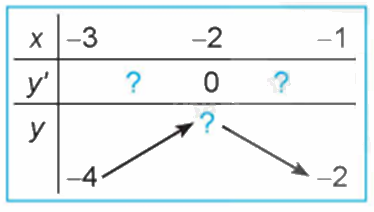
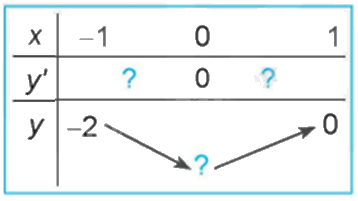
Phương pháp giải:
- Sử dụng kiến thức về định lí về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng K.
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) đồng biến trên khoảng K.
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) nghịch biến trên khoảng K.
Lời giải chi tiết:
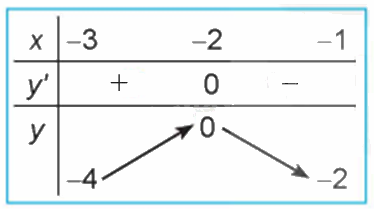
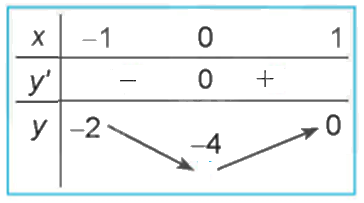
- HĐ4
- LT4
- HĐ5
- CH
- LT5
- VD2
Trả lời câu hỏi Hoạt động 4 trang 9 SGK Toán 12 Kết nối tri thức
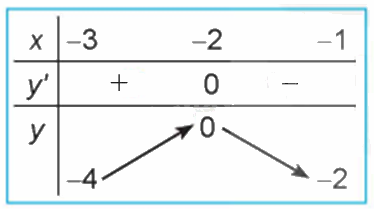
Quan sát đồ thị của hàm số \(y = {x^3} + 3{x^2} - 4\) (H.1.7). Xét dấu đạo hàm của hàm số đã cho và hoàn thành các bảng sau vào vở:
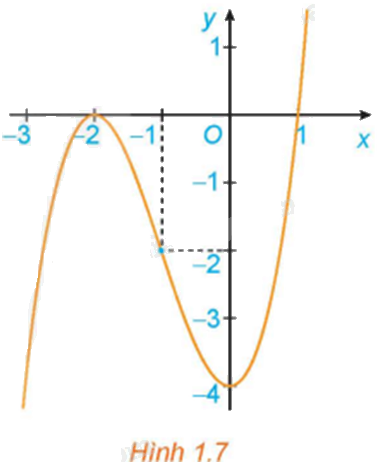
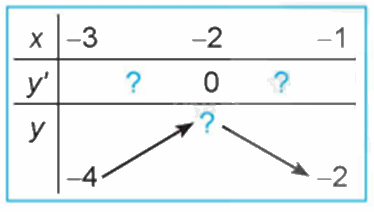
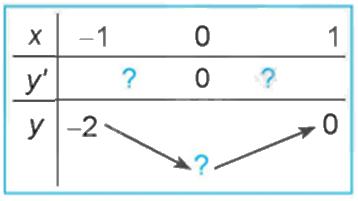
Phương pháp giải:
- Sử dụng kiến thức về định lí về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng K.
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) đồng biến trên khoảng K.
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) nghịch biến trên khoảng K.
Lời giải chi tiết:
Trả lời câu hỏi Luyện tập 4 trang 10 SGK Toán 12 Kết nối tri thức
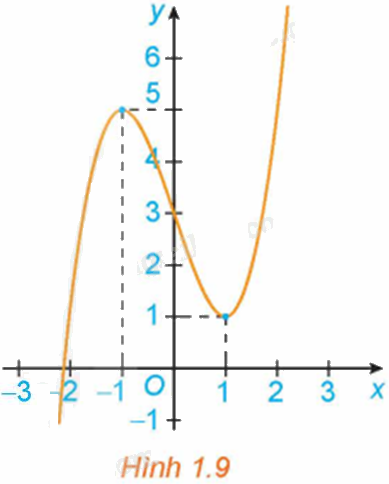
Hình 1.9 là đồ thị của hàm số \(y = f\left( x \right)\). Hãy tìm các cực trị của hàm số.
Phương pháp giải:
Sử dụng kiến thức về định nghĩa cực đại, cực tiểu của hàm số để tìm cực đại, cực tiểu của hàm số: Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên khoảng (a; b) (a có thể là \( - \infty \), b có thể là \( + \infty \)) và điểm \({x_0} \in \left( {a;b} \right)\).
+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) < f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực đại tại \({x_0}\).
+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) > f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực tiểu tại \({x_0}\).
Lời giải chi tiết:
Từ đồ thị hàm số, ta có:
Hàm số đạt cực tiểu tại \(x = 1\) và \({y_{CT}} = y\left( 1 \right) = 1\).
Hàm số đạt cực đại tại \(x = - 1\) và \({y_{C{\rm{D}}}} = y( - 1) = 5\)
Trả lời câu hỏi Hoạt động 5 trang 10 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 8x + 1\).
a) Tính đạo hàm \(f'\left( x \right)\) và tìm các điểm mà tại đó đạo hàm \(f'\left( x \right)\) bằng 0.
b) Lập bảng biến thiên của hàm số.
c) Từ bảng biến thiên suy ra các điểm cực trị của hàm số.
Phương pháp giải:
Sử dụng kiến thức về định nghĩa cực đại, cực tiểu của hàm số để tìm cực đại, cực tiểu của hàm số: Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên khoảng (a; b) (a có thể là \( - \infty \), b có thể là \( + \infty \)) và điểm \({x_0} \in \left( {a;b} \right)\).
+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) < f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực đại tại \({x_0}\).
+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) > f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực tiểu tại \({x_0}\).
Lời giải chi tiết:
a) Tập xác định: \(D = \mathbb{R}\).
\(y' = {x^2} - 6x + 8\), \(y' = 0 \Leftrightarrow {x^2} - 6x + 8 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = 2\end{array} \right.\)
Vậy \(x = 4;x = 2\) thì \(f'\left( x \right) = 0\)
b) Bảng biến thiên:
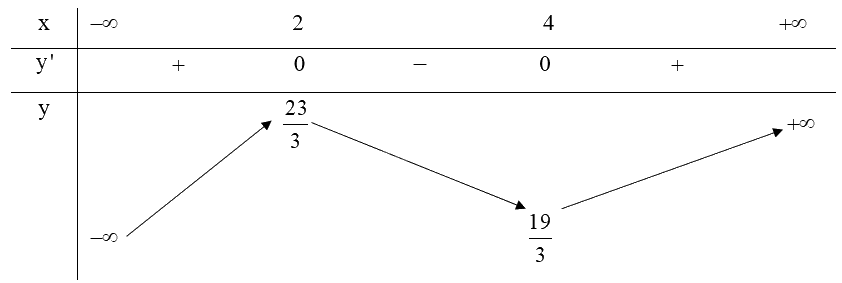
c) Từ bảng biến thiên ta có:
Hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 8x + 1\) có điểm cực đại là \(\left( {2;\frac{{23}}{3}} \right)\).
Hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 8x + 1\) có điểm cực tiểu là \(\left( {4;\frac{{19}}{3}} \right)\).
Trả lời câu hỏi trang 11 SGK Toán 12 Kết nối tri thức
Giải thích vì sao nếu f’(x) không đổi dấu qua \({x_0}\) thì \({x_0}\) không phải là điểm cực trị của hàm số f(x)?
Phương pháp giải:
Sử dụng kiến thức về định lí cực trị hàm số để chứng minh: Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Khi đó:
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực tiểu của hàm số f(x).
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực đại của hàm số f(x).d
Lời giải chi tiết:
Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Nếu f’(x) không đổi dấu qua \({x_0}\) thì:
TH1: \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\), ta có bảng biến thiên:
Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Nếu f’(x) không đổi dấu qua \({x_0}\) thì:
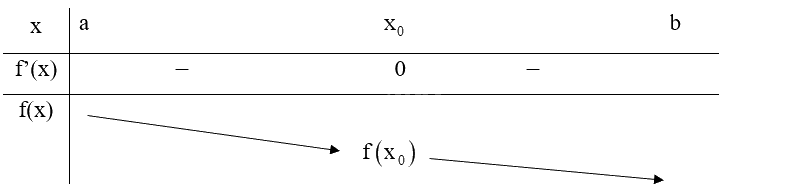
TH1: \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\), ta có bảng biến thiên:
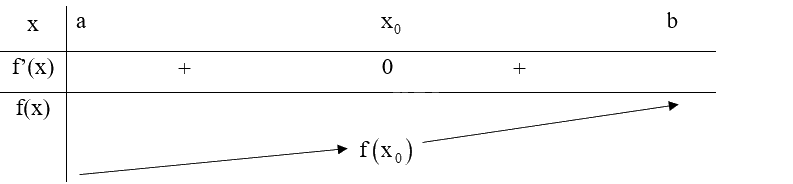
Do đó, \({x_0}\) không phải là điểm cực trị của hàm số f(x).
Trả lời câu hỏi Luyện tập 5 trang 12 SGK Toán 12 Kết nối tri thức
Tìm cực trị của các hàm số sau:
a) \(y = {x^4} - 3{x^2} + 1\);
b) \(y = \frac{{ - {x^2} + 2x - 1}}{{x + 2}}\).
Phương pháp giải:
Sử dụng kiến thức về cách tìm cực trị của hàm số \(y = f\left( x \right)\) để tìm cực trị của hàm số:
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.
Lời giải chi tiết:
a) Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \(y' = 4{x^3} - 6x,y' = 0 \Leftrightarrow 4{x^3} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \frac{{\sqrt 6 }}{2}\end{array} \right.\);
Bảng biến thiên:
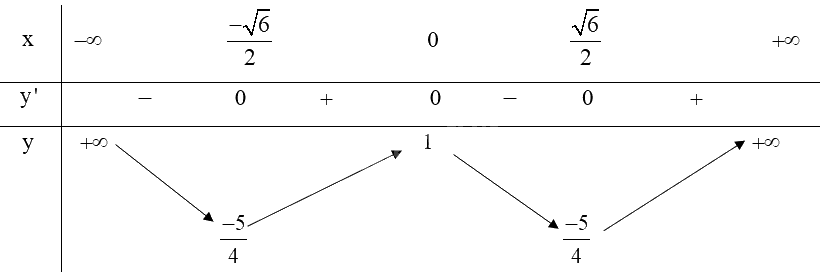
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại \(x = 0\) và .
Hàm số đạt cực tiểu tại \(x = \pm \frac{{\sqrt 6 }}{2}\) và \({y_{CT}} = \frac{{ - 5}}{4}\).
b) Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Ta có: \(y' = \frac{{\left( { - 2x + 2} \right)\left( {x + 2} \right) - \left( { - {x^2} + 2x - 1} \right)}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{ - {x^2} - 4x + 5}}{{{{\left( {x + 2} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 5\\x = 1\end{array} \right.\) (thỏa mãn)
Lập bảng biến thiên của hàm số:
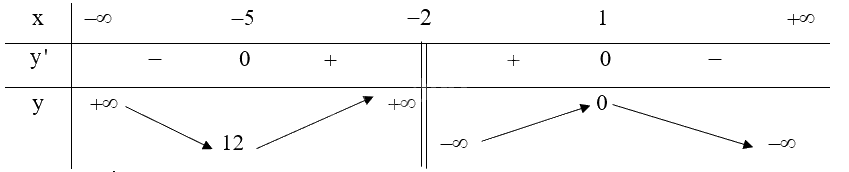
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại \(x = 1\) và .
Hàm số đạt cực tiểu tại \(x = - 5\) và \({y_{CT}} = 12\).
Trả lời câu hỏi Vận dụng 2 trang 12 SGK Toán 12 Kết nối tri thức
Một vật được phóng thẳng đứng lên trên từ độ cao 2m với vận tốc ban đầu là 24,5m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h (mét) của vật sau t (giây) được cho bởi công thức: \(h\left( t \right) = 2 + 24,5t - 4,9{t^2}\). Hỏi tại thời điểm nào thì vật đạt độ cao lớn nhất?
Phương pháp giải:
Sử dụng kiến thức về cách tìm cực trị của hàm số \(y = f\left( x \right)\) để tìm thời điểm vật đạt độ cao lớn nhất:
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.
Lời giải chi tiết:
Xét hàm số: \(h\left( t \right) = 2 + 24,5t - 4,9{t^2}\).
Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \[h'\left( t \right) = - 9,8t + 24,5;h'\left( t \right) = 0 \Leftrightarrow - 9,8t + 24,5 = 0 \Leftrightarrow t = \frac{5}{2}\].
Bảng biến thiên:
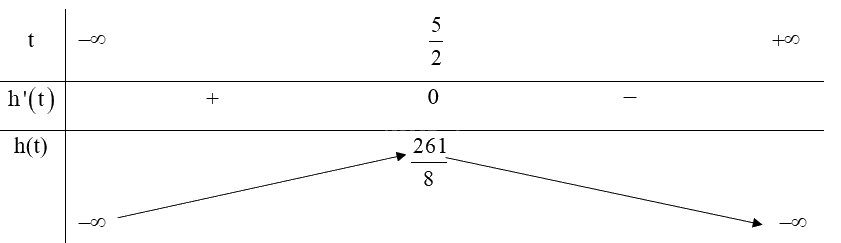
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại \(t = \frac{5}{2}\),
Vậy thời điểm vật đạt độ cao lớn nhất là \(t = \frac{5}{2}\) giây
Giải mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Kết nối tri thức: Tổng quan và Hướng dẫn chi tiết
Mục 2 của SGK Toán 12 tập 1 Kết nối tri thức tập trung vào việc ôn tập về hàm số và ứng dụng của đạo hàm trong việc khảo sát hàm số. Đây là một phần kiến thức nền tảng quan trọng, xuất hiện thường xuyên trong các bài thi THPT Quốc gia. Việc nắm vững kiến thức và kỹ năng giải bài tập trong mục này là điều cần thiết để đạt điểm cao.
Nội dung chính của Mục 2
- Ôn tập về hàm số: Định nghĩa hàm số, tập xác định, tập giá trị, tính đơn điệu, cực trị của hàm số.
- Ứng dụng đạo hàm: Khảo sát hàm số bằng đạo hàm, tìm cực trị, điểm uốn, vẽ đồ thị hàm số.
- Bài tập thực hành: Các bài tập áp dụng kiến thức đã học để giải quyết các bài toán cụ thể.
Giải chi tiết các bài tập trang 9
Trang 9 SGK Toán 12 tập 1 Kết nối tri thức thường chứa các bài tập về ôn tập khái niệm hàm số. Các bài tập này yêu cầu học sinh xác định tập xác định, tập giá trị, tính đơn điệu của hàm số. Ví dụ:
Bài 1: Xác định tập xác định của hàm số y = √(x-2)/(x+1).
Lời giải: Hàm số xác định khi và chỉ khi x-2 ≥ 0 và x+1 ≠ 0. Suy ra x ≥ 2 và x ≠ -1. Vậy tập xác định của hàm số là [2, +∞).
Giải chi tiết các bài tập trang 10
Trang 10 thường tập trung vào việc xét tính đơn điệu của hàm số bằng cách sử dụng đạo hàm. Học sinh cần tính đạo hàm, xét dấu đạo hàm và kết luận về tính đơn điệu của hàm số.
Bài 2: Xét tính đơn điệu của hàm số y = x3 - 3x2 + 2.
Lời giải: y' = 3x2 - 6x = 3x(x-2). y' = 0 khi x = 0 hoặc x = 2. Xét dấu y':
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | NB | Đ | CT |
Vậy hàm số đồng biến trên (-∞, 0) và (2, +∞), nghịch biến trên (0, 2).
Giải chi tiết các bài tập trang 11
Trang 11 thường chứa các bài tập về tìm cực trị của hàm số. Học sinh cần tìm điểm dừng, xét dấu đạo hàm bậc hai để xác định cực đại, cực tiểu.
Bài 3: Tìm cực đại, cực tiểu của hàm số y = x4 - 4x2 + 3.
Lời giải: y' = 4x3 - 8x = 4x(x2 - 2). y' = 0 khi x = 0, x = √2, x = -√2. y'' = 12x2 - 8. Tại x = 0, y'' = -8 < 0 => Hàm số đạt cực đại tại x = 0, y(0) = 3. Tại x = √2, y'' = 16 > 0 => Hàm số đạt cực tiểu tại x = √2, y(√2) = -1. Tại x = -√2, y'' = 16 > 0 => Hàm số đạt cực tiểu tại x = -√2, y(-√2) = -1.
Lời khuyên khi giải bài tập Mục 2
- Nắm vững định nghĩa và các tính chất của hàm số.
- Thành thạo các kỹ năng tính đạo hàm.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi, phần mềm vẽ đồ thị để kiểm tra kết quả.
Tusach.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em sẽ tự tin hơn trong việc giải các bài tập Mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 Kết nối tri thức. Chúc các em học tốt!