Giải mục 2 trang 49, 50, 51 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 2 trang 49, 50, 51 SGK Toán 12 tập 1 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 49, 50, 51 SGK Toán 12 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác và phương pháp giải bài tập một cách dễ hiểu nhất.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, tusach.vn luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ các em học tập hiệu quả.
Tổng và hiệu của hai vectơ trong không gian
LT3
Trả lời câu hỏi Luyện tập 3 trang 50 SGK Toán 12 Kết nối tri thức
Trong Ví dụ 3, hãy tính độ dài của vectơ \(\overrightarrow {AC} + \overrightarrow {C'D'} \).
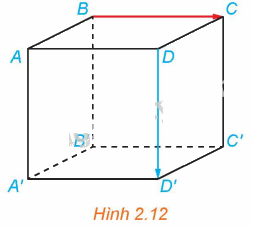
Ví dụ 3: Cho hình lập phương ABCD.A’B’C’D’ có độ dài mỗi cạnh bằng 1 (H.2.12).
Phương pháp giải:
Sử dụng kiến thức về quy tắc ba điểm để tính: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết:
Vì ABCD.A’B’C’D’ là hình lập phương nên DCC’D’ là hình vuông. Do đó, \(\overrightarrow {C'D'} = \overrightarrow {CD} \).
Ta có: \(\overrightarrow {AC} + \overrightarrow {C'D'} = \overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {AD} \)
Vì độ dài mỗi cạnh hình lập phương ABCD.A’B’C’D’ bằng 1 nên \(\left| {\overrightarrow {AD} } \right| = 1\).
Vậy \(\left| {\overrightarrow {AC} + \overrightarrow {C'D'} } \right| = 1\)
LT4
Trả lời câu hỏi Luyện tập 4 trang 50SGK Toán 12 Kết nối tri thức
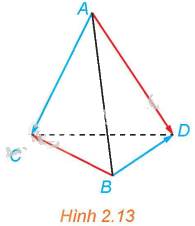
Cho tứ diện ABCD (H.2.13). Chứng minh rằng \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \).
Phương pháp giải:
Sử dụng kiến thức về quy tắc ba điểm để tính: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết:
Ta có: \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {DB} + \overrightarrow {CB} + \overrightarrow {BD} = \left( {\overrightarrow {AD} + \overrightarrow {CB} } \right) + \left( {\overrightarrow {DB} + \overrightarrow {BD} } \right)\)
\( = \overrightarrow {AD} + \overrightarrow {CB} + \overrightarrow {DD} = \overrightarrow {AD} + \overrightarrow {CB} \) (đpcm)
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 49SGK Toán 12 Kết nối tri thức
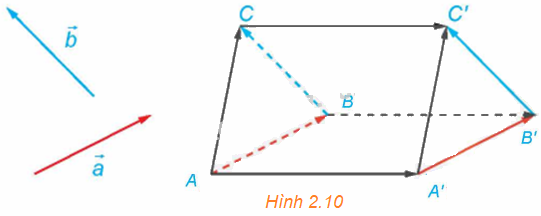
Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương. Lấy điểm A và vẽ các vectơ \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \). Lấy điểm A’ và vẽ các vectơ \(\overrightarrow {A'B'} = \overrightarrow a ,\overrightarrow {B'C'} = \overrightarrow b \) (H.2.10).
a) Giải thích vì sao \(\overrightarrow {AA'} = \overrightarrow {BB'} \) và \(\overrightarrow {BB'} = \overrightarrow {CC'} \).
b) Giải thích vì sao AA’C’C là hình bình hành, từ đó suy ra \(\overrightarrow {AC} = \overrightarrow {A'C'} \).
Phương pháp giải:
Sử dụng kiến thức về hai vectơ bằng nhau để giải thích: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
a) Vì \(\overrightarrow {AB} = \overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng và cùng độ dài.
Vì \(\overrightarrow {A'B'} = \overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow {A'B'} \) cùng hướng và cùng độ dài.
Do đó, hai vectơ \(\overrightarrow {A'B'} \) và \(\overrightarrow {AB} \) cùng hướng và cùng độ dài. Suy ra, AB//A’B’ và \(AB = A'B'\). Do đó, tứ giác ABB’A’ là hình bình hành. Suy ra, AA’//BB’ và \(AA' = BB' \Rightarrow \) hai vectơ \(\overrightarrow {AA'} ,\overrightarrow {BB'} \) có cùng hướng và cùng độ dài. Suy ra, \(\overrightarrow {AA'} = \overrightarrow {BB'} \).
Vì \(\overrightarrow {BC} = \overrightarrow b \) nên hai vectơ \(\overrightarrow b \) và \(\overrightarrow {BC} \) cùng hướng và cùng độ dài.
Vì \(\overrightarrow {B'C'} = \overrightarrow b \) nên hai vectơ \(\overrightarrow b \) và \(\overrightarrow {B'C'} \) cùng hướng và cùng độ dài.
Do đó, hai vectơ \(\overrightarrow {BC} \) và \(\overrightarrow {B'C'} \) cùng hướng và cùng độ dài. Suy ra, BC//B’C’ và \(BC = B'C'\). Do đó, tứ giác CBB’C’ là hình bình hành. Suy ra, CC’//BB’ và \(CC' = BB' \Rightarrow \) hai vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} \) có cùng hướng và cùng độ dài. Suy ra, \(\overrightarrow {BB'} = \overrightarrow {CC'} \).
b) Vì hai vectơ \(\overrightarrow {AA'} ,\overrightarrow {BB'} \) có cùng hướng và cùng độ dài; hai vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} \) có cùng hướng và cùng độ dài nên hai vectơ \(\overrightarrow {AA'} \) và \(\overrightarrow {CC'} \) có cùng hướng và cùng độ dài. Do đó, AA’//CC’ và \(AA' = CC'\) nên tứ giác AA’C’C là hình bình hành. Suy ra, \(AC = A'C'\) và AC//A’C’. Do đó, hai vectơ \(\overrightarrow {AC} ,\overrightarrow {A'C'} \) có cùng hướng và cùng độ dài. Suy ra, \(\overrightarrow {AC} = \overrightarrow {A'C'} \).
LT6
Trả lời câu hỏi Luyện tập 6 trang 52SGK Toán 12 Kết nối tri thức
Trong Ví dụ 6, chứng minh rằng:
a) \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) là hai vectơ đối nhau;
b) \(\overrightarrow {SD} - \overrightarrow {BN} - \overrightarrow {CM} = \overrightarrow {SC} \)
Phương pháp giải:
a) Sử dụng kiến thức về hai vectơ đối nhau để chứng minh: Trong không gian, vectơ có cùng độ dài và ngược hướng với vectơ \(\overrightarrow a \) được gọi là vectơ đối của vectơ \(\overrightarrow a \), kí hiệu là \( - \overrightarrow a \).
b) Sử dụng kiến thức về quy tắc ba điểm để chứng minh: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết:
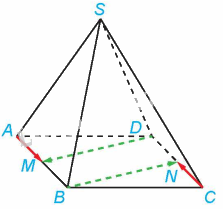
a) Tứ giác ABCD là hình bình hành nên \(AB = CD\), AB//CD. Suy ra \(BM = DN\) (vì M, N lần lượt là trung điểm của AB và CD) và BM//DN. Do đó, tứ giác DMBN là hình bình hành, do đó, \(BN = DM\) và BN//DM. Hai vectơ \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) có cùng độ dài và ngược hướng nên \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) là hai vectơ đối nhau.
b) Theo a ta có: \(\overrightarrow {BN} = - \overrightarrow {DM} \)
Do đó, \(\overrightarrow {SD} - \overrightarrow {BN} - \overrightarrow {CM} = \overrightarrow {SD} + \overrightarrow {DM} + \overrightarrow {MC} = \overrightarrow {SM} + \overrightarrow {MC} = \overrightarrow {SC} \)
LT5
Trả lời câu hỏi Luyện tập 5 trang 50SGK Toán 12 Kết nối tri thức
Cho hình hộp hình chữ nhật ABCD.A’B’C’D’. Chứng minh rằng \(\overrightarrow {BB'} + \overrightarrow {CD} + \overrightarrow {AD} = \overrightarrow {BD'} \)
Phương pháp giải:
Sử dụng kiến thức về quy tắc hình hộp để giải: Cho hình hộp ABCD.A’B’C’D’. Khi đó, ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
Lời giải chi tiết:
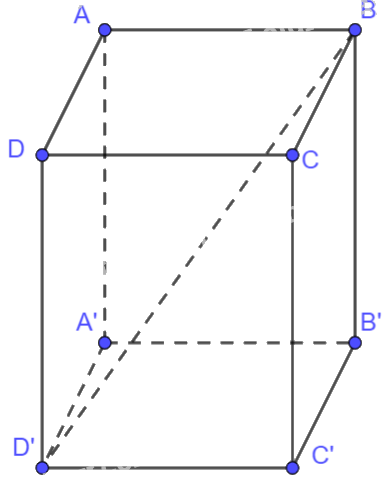
Vì ABCD là hình chữ nhật nên \(\overrightarrow {AD} = \overrightarrow {BC} ,\overrightarrow {CD} = \overrightarrow {BA} \)
Vì ABCD.A’B’C’D’ là hình hộp chữ nhật nên \(\overrightarrow {BB'} + \overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BD'} \)
Ta có: \(\overrightarrow {BB'} + \overrightarrow {CD} + \overrightarrow {AD} = \overrightarrow {BB'} + \overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BD'} \)
CH
Trả lời câu hỏi Câu hỏi trang 50SGK Toán 12 Kết nối tri thức
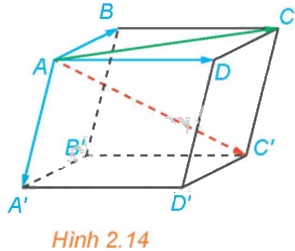
Trong Hình 2.14, hãy phát biểu quy tắc hình hộp với các vectơ có điểm đầu là B.
Phương pháp giải:
Sử dụng kiến thức về quy tắc hình hộp để giải bài toán: Cho hình hộp ABCD.A’B’C’D’. Khi đó, ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
Lời giải chi tiết:
Quy tắc hình hộp với các vectơ có điểm đầu là B là: \(\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD'} \)
HĐ4
Trả lời câu hỏi Hoạt động 4 trang 50SGK Toán 12 Kết nối tri thức
Cho hình hộp ABCD.A’B’C’D’ (H.2.14).
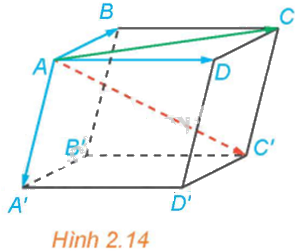
a) Hai vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \) và \(\overrightarrow {AC} \) có bằng nhau hay không?
b) Hai vectơ \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \) và \(\overrightarrow {AC'} \) có bằng nhau hay không?
Phương pháp giải:
Sử dụng quy tắc hình bình hành để chứng minh: Nếu ABCD là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Lời giải chi tiết:
a) Vì ABCD là hình bình hành nên \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
b) Ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC} + \overrightarrow {AA'} \) (1)
Vì ABCD. A’B’C’D’ là hình hộp nên AA’D’D và DD’C’C là hình bình hành. Do đó, AA’//DD’, \(AA' = DD'\) và \(DD' = CC'\), DD’//CC’. Suy ra, AA’//CC’ và \(AA' = CC'\). Suy ra, tứ giác AA’C’C là hình bình hành. Suy ra: \(\overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \) (2)
Từ (1) và (2) ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
HĐ5
Trả lời câu hỏi Hoạt động 5 trang 51SGK Toán 12 Kết nối tri thức
Hình 2.15 mô tả một lọ hoa được đặt trên bàn, trọng lượng của lọ hoa tạo nên một lực tác dụng lên mặt bàn và một phản lực từ mặt bàn lên lọ hoa. Có nhận xét về độ dài và hướng của các vectơ biểu diễn hai lực đó.

Phương pháp giải:
Sử dụng kiến thức về Định luật III Newton để giải thích: Lực tác dụng và phản lực là hai lực cùng phương, ngược hướng và có độ lớn bằng nhau.
Lời giải chi tiết:
Các vectơ biểu diễn hai lực đó có độ dài bằng nhau và hướng của chúng là ngược nhau.
VD2
Trả lời câu hỏi Vận dụng 2 trang 52SGK Toán 12 Kết nối tri thức
Thang cuốn tại các trung tâm thương mại, siêu thị hay nhà ga, sân bay thường có hai làn, trong đó một làn lên và một làn xuống. Khi thang cuốn chuyển động, vectơ biểu diễn vận tốc của mỗi làn có là hai vectơ đối nhau không? Giải thích vì sao.

Phương pháp giải:
Sử dụng kiến thức về hai vectơ đối nhau để giải thích: Trong không gian, vectơ có cùng độ dài và ngược hướng với vectơ \(\overrightarrow a \) được gọi là vectơ đối của vectơ \(\overrightarrow a \), kí hiệu là \( - \overrightarrow a \).
Lời giải chi tiết:
Vectơ biểu diễn vận tốc của mỗi làn có cùng độ lớn và hướng ngược nhau nên chúng là hai vectơ đối nhau.
- HĐ3
- LT3
- LT4
- HĐ4
- CH
- LT5
- HĐ5
- LT6
- VD2
Trả lời câu hỏi Hoạt động 3 trang 49SGK Toán 12 Kết nối tri thức
Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương. Lấy điểm A và vẽ các vectơ \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \). Lấy điểm A’ và vẽ các vectơ \(\overrightarrow {A'B'} = \overrightarrow a ,\overrightarrow {B'C'} = \overrightarrow b \) (H.2.10).
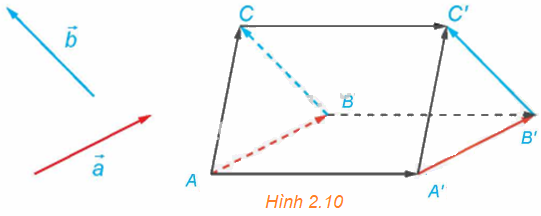
a) Giải thích vì sao \(\overrightarrow {AA'} = \overrightarrow {BB'} \) và \(\overrightarrow {BB'} = \overrightarrow {CC'} \).
b) Giải thích vì sao AA’C’C là hình bình hành, từ đó suy ra \(\overrightarrow {AC} = \overrightarrow {A'C'} \).
Phương pháp giải:
Sử dụng kiến thức về hai vectơ bằng nhau để giải thích: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
a) Vì \(\overrightarrow {AB} = \overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng và cùng độ dài.
Vì \(\overrightarrow {A'B'} = \overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow {A'B'} \) cùng hướng và cùng độ dài.
Do đó, hai vectơ \(\overrightarrow {A'B'} \) và \(\overrightarrow {AB} \) cùng hướng và cùng độ dài. Suy ra, AB//A’B’ và \(AB = A'B'\). Do đó, tứ giác ABB’A’ là hình bình hành. Suy ra, AA’//BB’ và \(AA' = BB' \Rightarrow \) hai vectơ \(\overrightarrow {AA'} ,\overrightarrow {BB'} \) có cùng hướng và cùng độ dài. Suy ra, \(\overrightarrow {AA'} = \overrightarrow {BB'} \).
Vì \(\overrightarrow {BC} = \overrightarrow b \) nên hai vectơ \(\overrightarrow b \) và \(\overrightarrow {BC} \) cùng hướng và cùng độ dài.
Vì \(\overrightarrow {B'C'} = \overrightarrow b \) nên hai vectơ \(\overrightarrow b \) và \(\overrightarrow {B'C'} \) cùng hướng và cùng độ dài.
Do đó, hai vectơ \(\overrightarrow {BC} \) và \(\overrightarrow {B'C'} \) cùng hướng và cùng độ dài. Suy ra, BC//B’C’ và \(BC = B'C'\). Do đó, tứ giác CBB’C’ là hình bình hành. Suy ra, CC’//BB’ và \(CC' = BB' \Rightarrow \) hai vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} \) có cùng hướng và cùng độ dài. Suy ra, \(\overrightarrow {BB'} = \overrightarrow {CC'} \).
b) Vì hai vectơ \(\overrightarrow {AA'} ,\overrightarrow {BB'} \) có cùng hướng và cùng độ dài; hai vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} \) có cùng hướng và cùng độ dài nên hai vectơ \(\overrightarrow {AA'} \) và \(\overrightarrow {CC'} \) có cùng hướng và cùng độ dài. Do đó, AA’//CC’ và \(AA' = CC'\) nên tứ giác AA’C’C là hình bình hành. Suy ra, \(AC = A'C'\) và AC//A’C’. Do đó, hai vectơ \(\overrightarrow {AC} ,\overrightarrow {A'C'} \) có cùng hướng và cùng độ dài. Suy ra, \(\overrightarrow {AC} = \overrightarrow {A'C'} \).
Trả lời câu hỏi Luyện tập 3 trang 50 SGK Toán 12 Kết nối tri thức
Trong Ví dụ 3, hãy tính độ dài của vectơ \(\overrightarrow {AC} + \overrightarrow {C'D'} \).
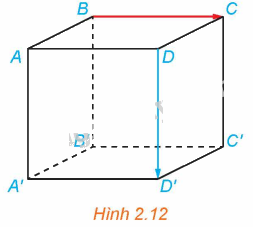
Ví dụ 3: Cho hình lập phương ABCD.A’B’C’D’ có độ dài mỗi cạnh bằng 1 (H.2.12).
Phương pháp giải:
Sử dụng kiến thức về quy tắc ba điểm để tính: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết:
Vì ABCD.A’B’C’D’ là hình lập phương nên DCC’D’ là hình vuông. Do đó, \(\overrightarrow {C'D'} = \overrightarrow {CD} \).
Ta có: \(\overrightarrow {AC} + \overrightarrow {C'D'} = \overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {AD} \)
Vì độ dài mỗi cạnh hình lập phương ABCD.A’B’C’D’ bằng 1 nên \(\left| {\overrightarrow {AD} } \right| = 1\).
Vậy \(\left| {\overrightarrow {AC} + \overrightarrow {C'D'} } \right| = 1\)
Trả lời câu hỏi Luyện tập 4 trang 50SGK Toán 12 Kết nối tri thức
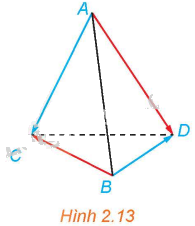
Cho tứ diện ABCD (H.2.13). Chứng minh rằng \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \).
Phương pháp giải:
Sử dụng kiến thức về quy tắc ba điểm để tính: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết:
Ta có: \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {DB} + \overrightarrow {CB} + \overrightarrow {BD} = \left( {\overrightarrow {AD} + \overrightarrow {CB} } \right) + \left( {\overrightarrow {DB} + \overrightarrow {BD} } \right)\)
\( = \overrightarrow {AD} + \overrightarrow {CB} + \overrightarrow {DD} = \overrightarrow {AD} + \overrightarrow {CB} \) (đpcm)
Trả lời câu hỏi Hoạt động 4 trang 50SGK Toán 12 Kết nối tri thức
Cho hình hộp ABCD.A’B’C’D’ (H.2.14).
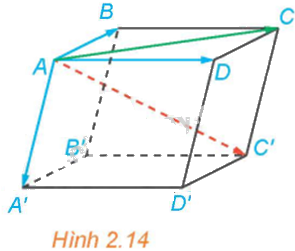
a) Hai vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \) và \(\overrightarrow {AC} \) có bằng nhau hay không?
b) Hai vectơ \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \) và \(\overrightarrow {AC'} \) có bằng nhau hay không?
Phương pháp giải:
Sử dụng quy tắc hình bình hành để chứng minh: Nếu ABCD là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Lời giải chi tiết:
a) Vì ABCD là hình bình hành nên \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
b) Ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC} + \overrightarrow {AA'} \) (1)
Vì ABCD. A’B’C’D’ là hình hộp nên AA’D’D và DD’C’C là hình bình hành. Do đó, AA’//DD’, \(AA' = DD'\) và \(DD' = CC'\), DD’//CC’. Suy ra, AA’//CC’ và \(AA' = CC'\). Suy ra, tứ giác AA’C’C là hình bình hành. Suy ra: \(\overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \) (2)
Từ (1) và (2) ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
Trả lời câu hỏi Câu hỏi trang 50SGK Toán 12 Kết nối tri thức
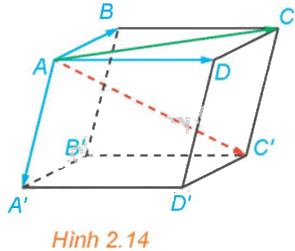
Trong Hình 2.14, hãy phát biểu quy tắc hình hộp với các vectơ có điểm đầu là B.
Phương pháp giải:
Sử dụng kiến thức về quy tắc hình hộp để giải bài toán: Cho hình hộp ABCD.A’B’C’D’. Khi đó, ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
Lời giải chi tiết:
Quy tắc hình hộp với các vectơ có điểm đầu là B là: \(\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD'} \)
Trả lời câu hỏi Luyện tập 5 trang 50SGK Toán 12 Kết nối tri thức
Cho hình hộp hình chữ nhật ABCD.A’B’C’D’. Chứng minh rằng \(\overrightarrow {BB'} + \overrightarrow {CD} + \overrightarrow {AD} = \overrightarrow {BD'} \)
Phương pháp giải:
Sử dụng kiến thức về quy tắc hình hộp để giải: Cho hình hộp ABCD.A’B’C’D’. Khi đó, ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
Lời giải chi tiết:
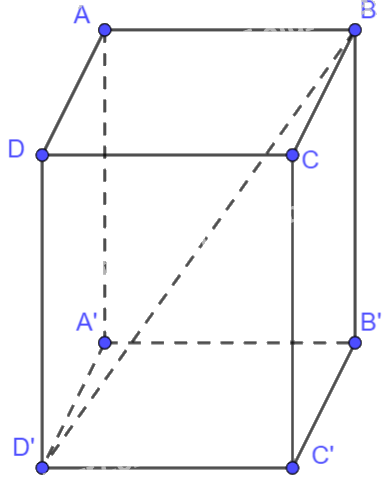
Vì ABCD là hình chữ nhật nên \(\overrightarrow {AD} = \overrightarrow {BC} ,\overrightarrow {CD} = \overrightarrow {BA} \)
Vì ABCD.A’B’C’D’ là hình hộp chữ nhật nên \(\overrightarrow {BB'} + \overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BD'} \)
Ta có: \(\overrightarrow {BB'} + \overrightarrow {CD} + \overrightarrow {AD} = \overrightarrow {BB'} + \overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BD'} \)
Trả lời câu hỏi Hoạt động 5 trang 51SGK Toán 12 Kết nối tri thức
Hình 2.15 mô tả một lọ hoa được đặt trên bàn, trọng lượng của lọ hoa tạo nên một lực tác dụng lên mặt bàn và một phản lực từ mặt bàn lên lọ hoa. Có nhận xét về độ dài và hướng của các vectơ biểu diễn hai lực đó.

Phương pháp giải:
Sử dụng kiến thức về Định luật III Newton để giải thích: Lực tác dụng và phản lực là hai lực cùng phương, ngược hướng và có độ lớn bằng nhau.
Lời giải chi tiết:
Các vectơ biểu diễn hai lực đó có độ dài bằng nhau và hướng của chúng là ngược nhau.
Trả lời câu hỏi Luyện tập 6 trang 52SGK Toán 12 Kết nối tri thức
Trong Ví dụ 6, chứng minh rằng:
a) \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) là hai vectơ đối nhau;
b) \(\overrightarrow {SD} - \overrightarrow {BN} - \overrightarrow {CM} = \overrightarrow {SC} \)
Phương pháp giải:
a) Sử dụng kiến thức về hai vectơ đối nhau để chứng minh: Trong không gian, vectơ có cùng độ dài và ngược hướng với vectơ \(\overrightarrow a \) được gọi là vectơ đối của vectơ \(\overrightarrow a \), kí hiệu là \( - \overrightarrow a \).
b) Sử dụng kiến thức về quy tắc ba điểm để chứng minh: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết:
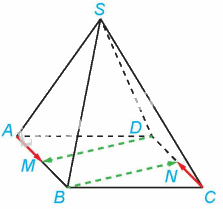
a) Tứ giác ABCD là hình bình hành nên \(AB = CD\), AB//CD. Suy ra \(BM = DN\) (vì M, N lần lượt là trung điểm của AB và CD) và BM//DN. Do đó, tứ giác DMBN là hình bình hành, do đó, \(BN = DM\) và BN//DM. Hai vectơ \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) có cùng độ dài và ngược hướng nên \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) là hai vectơ đối nhau.
b) Theo a ta có: \(\overrightarrow {BN} = - \overrightarrow {DM} \)
Do đó, \(\overrightarrow {SD} - \overrightarrow {BN} - \overrightarrow {CM} = \overrightarrow {SD} + \overrightarrow {DM} + \overrightarrow {MC} = \overrightarrow {SM} + \overrightarrow {MC} = \overrightarrow {SC} \)
Trả lời câu hỏi Vận dụng 2 trang 52SGK Toán 12 Kết nối tri thức
Thang cuốn tại các trung tâm thương mại, siêu thị hay nhà ga, sân bay thường có hai làn, trong đó một làn lên và một làn xuống. Khi thang cuốn chuyển động, vectơ biểu diễn vận tốc của mỗi làn có là hai vectơ đối nhau không? Giải thích vì sao.

Phương pháp giải:
Sử dụng kiến thức về hai vectơ đối nhau để giải thích: Trong không gian, vectơ có cùng độ dài và ngược hướng với vectơ \(\overrightarrow a \) được gọi là vectơ đối của vectơ \(\overrightarrow a \), kí hiệu là \( - \overrightarrow a \).
Lời giải chi tiết:
Vectơ biểu diễn vận tốc của mỗi làn có cùng độ lớn và hướng ngược nhau nên chúng là hai vectơ đối nhau.
Giải mục 2 trang 49, 50, 51 SGK Toán 12 tập 1 - Kết nối tri thức: Tổng quan và Hướng dẫn chi tiết
Mục 2 của SGK Toán 12 tập 1 Kết nối tri thức tập trung vào việc nghiên cứu hàm số và các khái niệm liên quan. Đây là một phần quan trọng trong chương trình học, đặt nền móng cho các kiến thức nâng cao hơn trong các lớp học tiếp theo. Việc nắm vững kiến thức trong mục này sẽ giúp học sinh giải quyết các bài toán một cách hiệu quả và tự tin hơn.
Nội dung chính của Mục 2
Mục 2 bao gồm các nội dung chính sau:
- Khái niệm hàm số: Định nghĩa hàm số, tập xác định, tập giá trị.
- Các loại hàm số: Hàm số chẵn, hàm số lẻ, hàm số đồng biến, hàm số nghịch biến.
- Đồ thị hàm số: Cách vẽ đồ thị hàm số, các tính chất của đồ thị.
- Ứng dụng của hàm số: Giải các bài toán thực tế liên quan đến hàm số.
Giải chi tiết bài tập trang 49
Bài 1: (Trang 49) Xác định tập xác định của hàm số f(x) = √(x-2).
Lời giải: Hàm số f(x) xác định khi và chỉ khi x - 2 ≥ 0, tức là x ≥ 2. Vậy tập xác định của hàm số là D = [2, +∞).
Bài 2: (Trang 49) Xét tính chẵn, lẻ của hàm số f(x) = x2 + 1.
Lời giải: Ta có f(-x) = (-x)2 + 1 = x2 + 1 = f(x). Vậy hàm số f(x) là hàm số chẵn.
Giải chi tiết bài tập trang 50
Bài 3: (Trang 50) Vẽ đồ thị của hàm số y = 2x + 1.
Lời giải: Đồ thị của hàm số y = 2x + 1 là một đường thẳng. Để vẽ đồ thị, ta xác định hai điểm thuộc đường thẳng, ví dụ: A(0, 1) và B(1, 3). Nối hai điểm này lại, ta được đồ thị của hàm số.
Giải chi tiết bài tập trang 51
Bài 4: (Trang 51) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = -x2 + 4x - 3 trên đoạn [-1, 3].
Lời giải: Hàm số y = -x2 + 4x - 3 là một hàm bậc hai có hệ số a = -1 < 0, nên hàm số đạt giá trị lớn nhất tại đỉnh của parabol. Hoành độ đỉnh là x = -b/(2a) = -4/(2*(-1)) = 2. Giá trị lớn nhất của hàm số là y(2) = -22 + 4*2 - 3 = 1. Để tìm giá trị nhỏ nhất, ta xét giá trị của hàm số tại hai đầu mút của đoạn [-1, 3]. Ta có y(-1) = -(-1)2 + 4*(-1) - 3 = -8 và y(3) = -32 + 4*3 - 3 = 0. Vậy giá trị nhỏ nhất của hàm số là -8.
Mẹo học tốt Toán 12
- Nắm vững kiến thức cơ bản: Đảm bảo bạn hiểu rõ các định nghĩa, khái niệm và công thức trong chương trình học.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Sử dụng tài liệu tham khảo: Tham khảo các sách giáo khoa, sách bài tập, đề thi và các nguồn tài liệu trực tuyến khác.
- Hỏi thầy cô giáo: Đừng ngần ngại hỏi thầy cô giáo nếu bạn gặp khó khăn trong quá trình học tập.
Kết luận
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên, các em học sinh đã có thể tự tin giải các bài tập mục 2 trang 49, 50, 51 SGK Toán 12 tập 1 Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong kỳ thi sắp tới!