Lý thuyết Khảo sát sự biến thiên và vẽ đồ thị của hàm số Toán 12 Kết nối tri thức
Tổng quan nội dung
Lý thuyết Khảo sát sự biến thiên và vẽ đồ thị hàm số Toán 12 Kết nối tri thức
Chương trình Toán 12 Kết nối tri thức tập trung vào việc giúp học sinh nắm vững phương pháp khảo sát hàm số, một kỹ năng quan trọng để giải quyết các bài toán liên quan đến hàm số và ứng dụng trong thực tế.
Bài viết này cung cấp đầy đủ lý thuyết, ví dụ minh họa và hướng dẫn chi tiết về cách vẽ đồ thị hàm số, giúp bạn tự tin đối mặt với các dạng bài tập khác nhau.
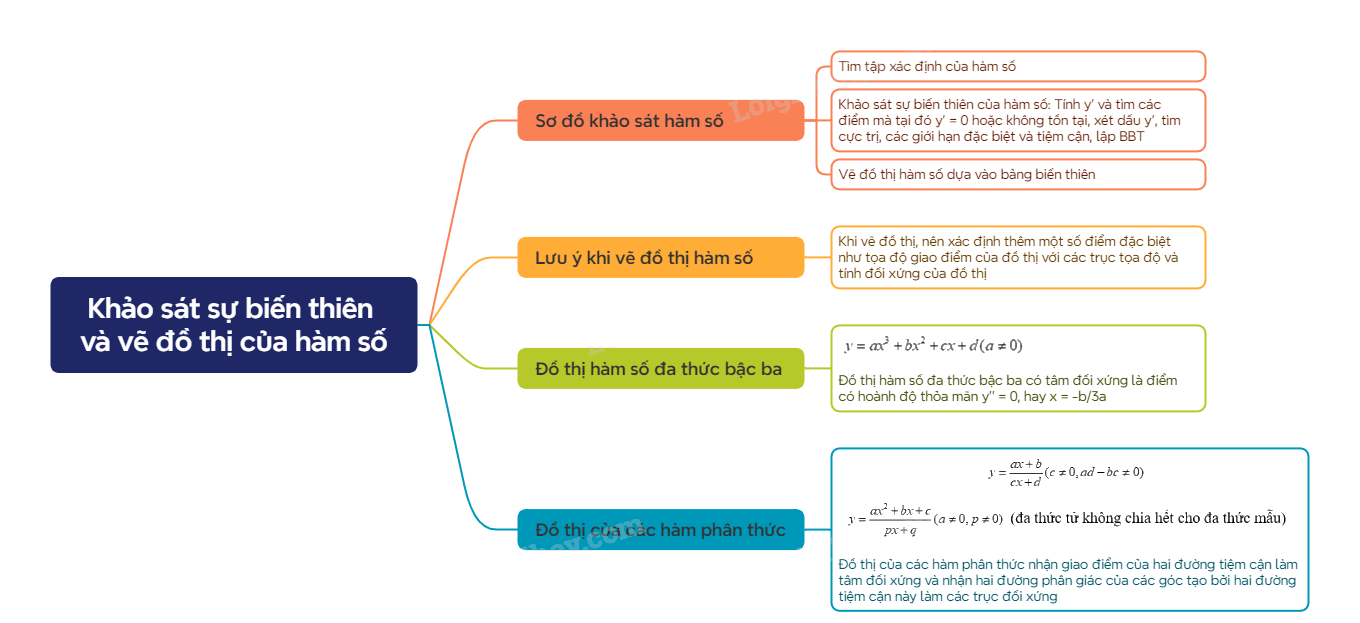
1. Sơ đồ khảo sát hàm số
1. Sơ đồ khảo sát hàm số
Các bước khảo sát hàm số
1. Tìm tập xác định của hàm số 2. Khảo sát sự biến thiên của hàm số - Tính đạo hàm y’. Tìm các điểm tại đó y’ = 0 hoặc đạo hàm không tồn tại - Xét dấu y’ để chỉ ra các khoảng đơn điệu của hàm số - Tìm cực trị của hàm số - Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận của đồ thị hàm số (nếu có) - Lập BBT của hàm số 3. Vẽ đồ thị của hàm số dựa vào BBT |
2. Khảo sát và vẽ đồ thị hàm số đa thức bậc ba
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = - {x^3} + 3{x^2} - 4\)
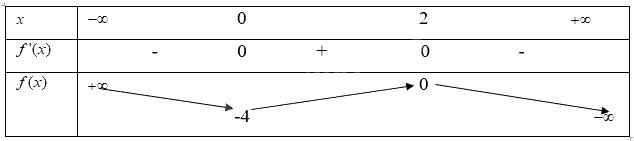
1. Tập xác định của hàm số: R
2. Sự biến thiên:
- Ta có: \(y' = - 3{x^2} + 6x\). Vậy y’ = 0 khi x = 0 hoặc x = 2
- Trên khoảng \(\left( {0;2} \right)\), y’ > 0 nên hàm số đồng biến. Trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\), y’ < 0 nên hàm số nghịch biến trên mỗi khoảng đó
- Hàm số đạt cực tiểu tại x = 0, giá trị cực tiểu \({y_{CT}} = - 4\). Hàm số đạt cực đại tại x = 2, giá trị cực đại
- Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = - \infty \)
- BBT:
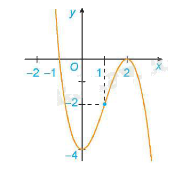
3. Đồ thị:
- Giao điểm của đồ thị hàm số với trục tung là điểm \(\left( {0;4} \right)\)
- Ta có: y = 0 \( \Leftrightarrow \)x = -1 hoặc x = 2. Do đó giao điểm của đồ thị hàm số với trục hoành là các điểm \(\left( { - 1;0} \right)\) và \(\left( {2;0} \right)\)
- Đồ thị hàm số có tâm đối xứng là điểm \(\left( {1; - 2} \right)\)
3. Khảo sát và vẽ đồ thị hàm số phân thức hữu tỷ
a) Hàm số phân thức \(y = \frac{{ax + b}}{{cx + d}}(c \ne 0,ad - bc \ne 0)\)
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{x + 1}}{{x - 2}}\)
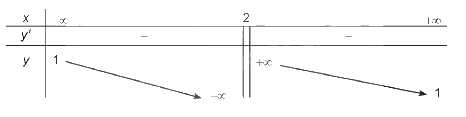
1. Tập xác định của hàm số: R\{2}
2. Sự biến thiên:
- Ta có: \(y' = - \frac{3}{{{{(x - 2)}^2}}} < 0\) với mọi \(x \ne 2\)
- Hàm số nghịch biến trên từng khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\)
- Hàm số không có cực trị
- Tiệm cận: \(\mathop {\lim }\limits_{x \to - \infty } y = 1;\mathop {\lim }\limits_{x \to + \infty } y = 1\)
\(\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty ;\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty \)
Do đó, đồ thị của hàm số có tiệm cận đứng là x = 2, tiệm cận ngang là y = 1
- BBT:
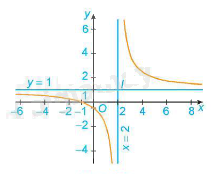
3. Đồ thị:
- Giao điểm của đồ thị hàm số với trục tung là điểm \(\left( {0; - \frac{1}{2}} \right)\)
- Giao điểm của đồ thị hàm số với trục hoành là điểm \(\left( { - 1;0} \right)\)
- Đồ thị hàm số nhận giao điểm I \(\left( {2;1} \right)\) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng
b) Hàm số phân thức \(y = \frac{{a{x^2} + bx + c}}{{px + q}}(a \ne 0,p \ne 0)\)(đa thức tử không chia hết cho đa thức mẫu)
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{{x^2} - x - 1}}{{x - 2}}\)
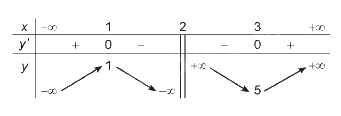
1. Tập xác định của hàm số: R\{2}
2. Sự biến thiên: Viết \(y = x + 1 + \frac{1}{{x - 2}}\)
- Ta có: \(y' = 1 - \frac{1}{{{{(x - 2)}^2}}} = \frac{{{x^2} - 4x + 3}}{{{{(x - 2)}^2}}}\) . Vậy y’ = 0 \( \Leftrightarrow \) x = 1 hoặc x = 3
- Trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {3; + \infty } \right)\), y’ > 0 nên hàm số đồng biến trên từng khoảng này
- Trên các khoảng \(\left( {1;2} \right)\) và \(\left( {2;3} \right)\), y’ < 0 nên hàm số nghịch biến trên từng khoảng này
- Hàm số đạt cực đại tại x = 1 với ; hàm số đạt cực tiểu tại x = 3 với \({y_{CT}} = 5\)
\(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\mathop {\lim }\limits_{x \to + \infty } y = + \infty \)
\(\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty ;\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x - 2}} = 0\); \(\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x - 2}} = 0\)
Do đó, đồ thị của hàm số có tiệm cận đứng là x = 2, tiệm cận xiên là y = x+1
- BBT:
3. Đồ thị:
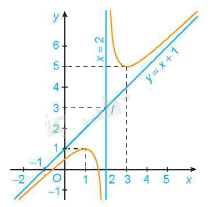
- Giao điểm của đồ thị hàm số với trục tung là điểm \(\left( {0;\frac{1}{2}} \right)\)
- Ta có: \(y = 0 \Leftrightarrow x = \frac{{1 - \sqrt 5 }}{2};x = \frac{{1 + \sqrt 5 }}{2}\). Do đó giao điểm của đồ thị hàm số với trục hoành là điểm \(\left( {\frac{{1 - \sqrt 5 }}{2};0} \right);\left( {\frac{{1 + \sqrt 5 }}{2};0} \right)\)
- Đồ thị hàm số nhận giao điểm I \(\left( {2;3} \right)\) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng
Lý Thuyết Khảo Sát Sự Biến Thiên và Vẽ Đồ Thị Hàm Số Toán 12 Kết Nối Tri Thức
Khảo sát sự biến thiên và vẽ đồ thị hàm số là một trong những nội dung quan trọng của chương trình Toán 12 Kết nối tri thức. Việc nắm vững lý thuyết và phương pháp thực hành sẽ giúp học sinh giải quyết hiệu quả các bài toán liên quan đến hàm số, đồng thời phát triển tư duy logic và khả năng phân tích.
I. Các Bước Khảo Sát Sự Biến Thiên của Hàm Số
- Xác định tập xác định: Tìm khoảng mà hàm số có nghĩa.
- Xét tính đơn điệu của hàm số:
- Tính đạo hàm f'(x).
- Giải phương trình f'(x) = 0 để tìm các điểm cực trị.
- Lập bảng xét dấu f'(x) để xác định khoảng đồng biến, nghịch biến.
- Tìm cực trị của hàm số: Xác định các điểm cực đại, cực tiểu và giá trị tương ứng.
- Tìm giới hạn vô cực: Xét giới hạn của hàm số khi x tiến tới vô cực và các giá trị đặc biệt.
- Tìm tiệm cận: Xác định các đường tiệm cận đứng, ngang và xiên (nếu có).
- Lập bảng biến thiên: Tổng hợp các thông tin đã tìm được vào bảng biến thiên.
II. Vẽ Đồ Thị Hàm Số
Sau khi khảo sát sự biến thiên, việc vẽ đồ thị hàm số trở nên dễ dàng hơn. Các bước thực hiện:
- Vẽ hệ trục tọa độ: Chọn hệ trục tọa độ phù hợp với hàm số.
- Đánh dấu các điểm đặc biệt: Đánh dấu các điểm cực trị, giao điểm với các trục tọa độ, tiệm cận.
- Vẽ đồ thị: Dựa vào bảng biến thiên và các điểm đặc biệt để vẽ đồ thị hàm số một cách chính xác.
III. Ví Dụ Minh Họa
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị hàm số y = x3 - 3x2 + 2.
Giải:
- Tập xác định: D = ℝ
- Đạo hàm: y' = 3x2 - 6x
- Giải phương trình y' = 0: 3x2 - 6x = 0 => x = 0 hoặc x = 2
- Bảng xét dấu y':
x -∞ 0 2 +∞ y' + - + Hàm số Đồng biến Nghịch biến Đồng biến - Cực trị: Hàm số đạt cực đại tại x = 0, y = 2 và cực tiểu tại x = 2, y = -2.
- Giới hạn vô cực: limx→+∞ y = +∞, limx→-∞ y = -∞
- Bảng biến thiên: (Tự lập)
Vẽ đồ thị: Dựa vào các thông tin trên, ta có thể vẽ được đồ thị hàm số y = x3 - 3x2 + 2.
IV. Lưu Ý Quan Trọng
- Luôn kiểm tra lại các bước tính toán để đảm bảo tính chính xác.
- Sử dụng công cụ vẽ đồ thị để kiểm tra kết quả.
- Luyện tập thường xuyên với nhiều dạng bài tập khác nhau để nắm vững phương pháp.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết khảo sát sự biến thiên và vẽ đồ thị hàm số Toán 12 Kết nối tri thức. Chúc bạn học tập tốt và đạt kết quả cao trong kỳ thi!