Giải bài tập 1.2 trang 13 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 1.2 Trang 13 Toán 12 Tập 1 - Kết Nối Tri Thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 12 tập 1 - Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn giải bài tập 1.2 trang 13 một cách dễ hiểu nhất.
Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Xét sự đồng biến, nghịch biến của các hàm số sau: a) (y = frac{1}{3}{x^3} - 2{x^2} + 3x + 1); b) (y = - {x^3} + 2{x^2} - 5x + 3).
Đề bài
Xét sự đồng biến, nghịch biến của các hàm số sau:
a) \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x + 1\);
b) \(y = - {x^3} + 2{x^2} - 5x + 3\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về các bước để xét tính đơn điệu để xét sự đồng biến, nghịch biến của hàm số: Các bước để xét tính đơn điệu của hàm số \(y = f\left( x \right)\):
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm \(f'\left( x \right)\). Tìm các điểm \({x_i}\left( {i = 1,2,...} \right)\) mà tại đó đạo hàm bằng 0 hoặc không tồn tại.
3. Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập bảng biến thiên của hàm số.
4. Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết
a) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = {x^2} - 4x + 3,y' = 0 \Leftrightarrow {x^2} - 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)
Lập bảng biến thiên của hàm số:
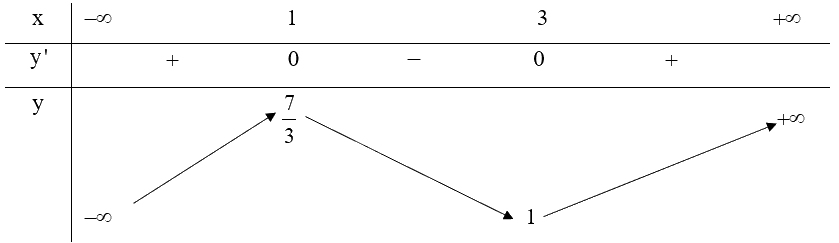
Hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x + 1\) đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {3; + \infty } \right)\).
Hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x + 1\) nghịch biến trên khoảng \(\left( {1;3} \right)\).
b) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = - 3{x^2} + 4x - 5\)
Vì \( - 3{x^2} + 4x - 5 = - 3\left( {{x^2} - 2.\frac{2}{3}.x + \frac{4}{9}} \right) - \frac{{11}}{3} = - 3{\left( {x - \frac{2}{3}} \right)^2} - \frac{{11}}{3} < 0\;\forall x \in \mathbb{R}\)
Do đó, \(y' < 0\;\forall x \in \mathbb{R}\).
Vậy hàm số \(y = - {x^3} + 2{x^2} - 5x + 3\) nghịch biến trên \(\left( { - \infty ; + \infty } \right)\).
Giải Bài Tập 1.2 Trang 13 Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 1.2 trang 13 SGK Toán 12 tập 1 Kết nối tri thức thuộc chương 1: Hàm số và đồ thị. Bài tập này thường xoay quanh việc xác định tập xác định của hàm số, tìm tập giá trị, và xét tính đơn điệu của hàm số. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Phần 1: Đề Bài Bài Tập 1.2 Trang 13
Trước khi đi vào giải, chúng ta cùng xem lại đề bài của bài tập 1.2 trang 13 SGK Toán 12 tập 1 Kết nối tri thức:
(Đề bài cụ thể của bài tập 1.2 sẽ được chèn vào đây. Ví dụ: Xác định tập xác định của hàm số f(x) = √(x-2)/(x+1))
Phần 2: Phương Pháp Giải
Để giải bài tập này, bạn cần nắm vững các kiến thức sau:
- Tập xác định của hàm số: Là tập hợp tất cả các giá trị của x sao cho hàm số f(x) có nghĩa.
- Điều kiện xác định của hàm số: Ví dụ, với hàm số chứa căn bậc chẵn, biểu thức dưới dấu căn phải lớn hơn hoặc bằng 0. Với hàm số phân thức, mẫu số khác 0.
- Các phép toán trên tập hợp: Giao, hợp, hiệu của các tập hợp.
Phần 3: Lời Giải Chi Tiết
Bước 1: Xác định điều kiện xác định của hàm số. (Giải thích cụ thể dựa trên đề bài)
Bước 2: Giải các bất phương trình hoặc phương trình để tìm ra các giá trị của x thỏa mãn điều kiện xác định. (Giải thích chi tiết các bước giải)
Bước 3: Viết tập xác định của hàm số dưới dạng ký hiệu tập hợp. (Ví dụ: D = {x | x > 2})
Phần 4: Ví Dụ Minh Họa
Ví dụ: Giải bài tập tương tự để củng cố kiến thức.
(Ví dụ cụ thể với lời giải chi tiết)
Phần 5: Luyện Tập Thêm
Để nắm vững hơn kiến thức về tập xác định của hàm số, bạn có thể luyện tập thêm với các bài tập sau:
- Bài tập 1.3 trang 13 SGK Toán 12 tập 1 Kết nối tri thức
- Bài tập 1.4 trang 14 SGK Toán 12 tập 1 Kết nối tri thức
Phần 6: Tổng Kết
Bài tập 1.2 trang 13 SGK Toán 12 tập 1 Kết nối tri thức là một bài tập cơ bản để làm quen với khái niệm tập xác định của hàm số. Việc nắm vững kiến thức và luyện tập thường xuyên sẽ giúp bạn giải quyết các bài tập tương tự một cách dễ dàng.
Lưu ý: Nếu bạn gặp khó khăn trong quá trình giải bài tập, đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè. tusach.vn luôn sẵn sàng hỗ trợ bạn!
Chúc bạn học tốt!
| Khái niệm | Giải thích |
|---|---|
| Tập xác định | Tập hợp các giá trị x để hàm số có nghĩa |
| Điều kiện xác định | Các ràng buộc về x để hàm số có nghĩa |
| Bảng tóm tắt các khái niệm quan trọng | |