Giải bài tập 2.18 trang 65 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 2.18 Trang 65 Toán 12 Tập 1 - Kết Nối Tri Thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 12 tập 1 - Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn giải bài tập 2.18 trang 65 một cách dễ hiểu nhất.
Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Trong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ có (Aleft( {1;1; - 1} right),Bleft( {0;3;0} right),C'left( {2; - 3;6} right)). a) Xác định tọa độ của điểm C. b) Xác định các tọa độ đỉnh còn lại của hình hộp.
Đề bài
Trong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ có \(A\left( {1;1; - 1} \right),B\left( {0;3;0} \right),C'\left( {2; - 3;6} \right)\).a) Xác định tọa độ của điểm C.b) Xác định các tọa độ đỉnh còn lại của hình hộp.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tọa độ của vectơ theo tọa độ hai đầu mút để tìm tọa độ vectơ: Trong không gian Oxyz, cho hai điểm \(M\left( {{x_M},{y_M},{z_M}} \right)\) và \(N\left( {{x_N};{y_N};{z_N}} \right)\).
Khi đó, \(\overrightarrow {MN} = \left( {{x_N} - {x_M};{y_N} - {y_M};{z_N} - {z_M}} \right)\).
Lời giải chi tiết
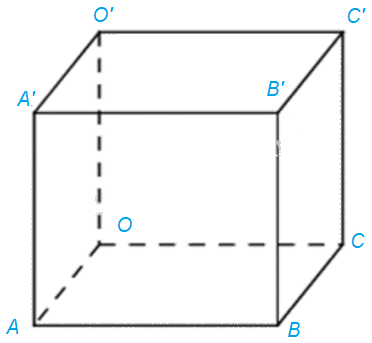
a) Ta có: O(0; 0; 0)
Vì OABC.O’A’B’C’ là hình hộp nên AOBC là hình bình hành. Do đó:\(\overrightarrow {OA} = \overrightarrow {CB} \Rightarrow \left\{ \begin{array}{l}{x_A} = {x_B} - {x_C}\\{y_A} = {y_B} - {y_C}\\{z_A} = {z_B} - {z_C}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_C} = {x_B} - {x_A} = -1\\{y_C} = {y_B} - {y_A} = 2\\{z_C} = {z_B} - {z_A} = 1\end{array} \right. \Rightarrow C\left( {-1; 2; 1} \right)\)
b) Vì OABC.O’A’B’C’ là hình hộp nên
\(\overrightarrow {OO'} = \overrightarrow {CC'} \Rightarrow \left\{ \begin{array}{l}{x_{O'}} = {x_{C'}} - {x_C} = 1\\{y_{O'}} = {y_{C'}} - {y_C} = - 1\\{z_{O'}} = {z_{C'}} - {z_C} = 7\end{array} \right. \Rightarrow O'\left( {1; - 1;7} \right)\)
\(\overrightarrow {AA'} = \overrightarrow {CC'} \Rightarrow \left\{ \begin{array}{l}{x_{A'}} - {x_A} = {x_{C'}} - {x_C} = 1\\{y_{A'}} - {y_A} = {y_{C'}} - {y_C} = - 1\\{z_{A'}} - {z_A} = {z_{C'}} - {z_C} = 7\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = 2\\{y_{A'}} = 0\\{z_{A'}} = 6\end{array} \right. \Rightarrow A'\left( {2;0;6} \right)\)
\(\overrightarrow {BB'} = \overrightarrow {CC'} \Rightarrow \left\{ \begin{array}{l}{x_{B'}} - {x_B} = \left( {{x_{C'}} - {x_C}} \right) = 1\\{y_{B'}} - {y_B} = \left( {{y_{C'}} - {y_C}} \right) = - 1\\{z_{B'}} - {z_B} = \left( {{z_{C'}} - {z_C}} \right) = 7\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_{B'}} = 1\\{y_{B'}} = 2\\{z_{B'}} = 7\end{array} \right. \Rightarrow B'\left( {1;2;7} \right)\)
Giải Bài Tập 2.18 Trang 65 Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 2.18 trang 65 SGK Toán 12 tập 1 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và các lưu ý quan trọng để bạn có thể hiểu rõ và áp dụng vào các bài tập tương tự.
Nội dung bài tập 2.18 trang 65 Toán 12 Tập 1 - Kết Nối Tri Thức
Bài tập 2.18 thường có dạng như sau: Cho hàm số f(x). Tính đạo hàm f'(x) và sử dụng đạo hàm để giải các bài toán liên quan đến việc tìm cực trị, khoảng đơn điệu, hoặc các bài toán ứng dụng khác.
Lời giải chi tiết bài tập 2.18 trang 65 Toán 12 Tập 1 - Kết Nối Tri Thức
Để giải bài tập này, chúng ta cần thực hiện các bước sau:
- Xác định hàm số f(x): Đọc kỹ đề bài để xác định chính xác hàm số f(x) cần xét.
- Tính đạo hàm f'(x): Sử dụng các quy tắc tính đạo hàm đã học (quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp,...) để tính đạo hàm f'(x).
- Giải phương trình f'(x) = 0: Giải phương trình f'(x) = 0 để tìm các điểm cực trị của hàm số.
- Xác định khoảng đơn điệu của hàm số: Dựa vào dấu của f'(x) trên các khoảng xác định của hàm số để xác định khoảng đồng biến và nghịch biến.
- Giải quyết các bài toán ứng dụng: Sử dụng đạo hàm để giải các bài toán ứng dụng liên quan đến việc tìm giá trị lớn nhất, giá trị nhỏ nhất, hoặc các bài toán tối ưu hóa khác.
Ví dụ minh họa (Giả định bài tập cụ thể)
Giả sử bài tập 2.18 yêu cầu chúng ta giải hàm số f(x) = x3 - 3x2 + 2.
Bước 1: Tính đạo hàm f'(x)
f'(x) = 3x2 - 6x
Bước 2: Giải phương trình f'(x) = 0
3x2 - 6x = 0
3x(x - 2) = 0
=> x = 0 hoặc x = 2
Bước 3: Xác định khoảng đơn điệu
- Khi x < 0: f'(x) > 0 => Hàm số đồng biến trên (-∞, 0)
- Khi 0 < x < 2: f'(x) < 0 => Hàm số nghịch biến trên (0, 2)
- Khi x > 2: f'(x) > 0 => Hàm số đồng biến trên (2, +∞)
Lưu ý quan trọng khi giải bài tập về đạo hàm
- Nắm vững các quy tắc tính đạo hàm.
- Kiểm tra kỹ kết quả tính đạo hàm.
- Sử dụng đạo hàm để phân tích tính chất của hàm số một cách chính xác.
- Luyện tập thường xuyên để nâng cao kỹ năng giải bài tập.
Các bài tập tương tự
Để củng cố kiến thức, bạn có thể tham khảo thêm các bài tập tương tự trong SGK Toán 12 tập 1 Kết nối tri thức và các tài liệu luyện tập khác.
Kết luận
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể giải bài tập 2.18 trang 65 SGK Toán 12 tập 1 Kết nối tri thức một cách dễ dàng và hiệu quả. Chúc bạn học tốt!
Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại để lại bình luận bên dưới. tusach.vn luôn sẵn sàng hỗ trợ bạn.