Giải bài tập 3.15 trang 86 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 3.15 Trang 86 Toán 12 Tập 1 - Kết Nối Tri Thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong SGK Toán 12 tập 1 - Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn giải bài tập 3.15 trang 86 một cách dễ hiểu nhất.
Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Người ta ghi lại tiền lãi (đơn vị: triệu đồng) của một số nhà đầu tư (với số tiền đầu tư như nhau), khi đầu tư vào hai lĩnh vực A, B cho kết quả như sau: a) Về trung bình, đầu tư vào lĩnh vực nào đem lại tiền lãi cao hơn? b) Tính độ lệch chuẩn cho các mẫu số liệu về tiền lãi của các nhà đầu tư ở hai lĩnh vực này và giải thích ý nghĩa của các số thu được.
Đề bài
Người ta ghi lại tiền lãi (đơn vị: triệu đồng) của một số nhà đầu tư (với số tiền đầu tư như nhau), khi đầu tư vào hai lĩnh vực A, B cho kết quả như sau: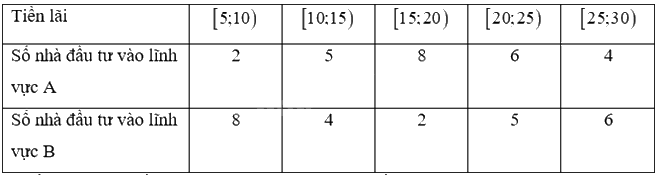
a) Về trung bình, đầu tư vào lĩnh vực nào đem lại tiền lãi cao hơn?
b) Tính độ lệch chuẩn cho các mẫu số liệu về tiền lãi của các nhà đầu tư ở hai lĩnh vực này và giải thích ý nghĩa của các số thu được.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về phương sai của mẫu số liệu ghép nhóm để tính: Phương sai của mẫu số liệu ghép nhóm, kí hiệu là \({s^2}\), là một số được tính theo công thức sau: \({s^2} = \frac{1}{n}\left( {{m_1}x_1^2 + ... + {m_k}x_k^2} \right) - {\left( {\overline x } \right)^2}\), trong đó \(n = {m_1} + ... + {m_k}\) với \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\) là số trung bình của mẫu số liệu ghép nhóm.
+ Sử dụng kiến thức độ lệch chuẩn của mẫu số liệu ghép nhóm để tính: Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \).
+ Sử dụng kiến thức về ý nghĩa của độ lệch chuẩn để giải thích: Độ lệch chuẩn của mẫu số liệu ghép nhóm càng lớn thì độ rủi ro càng lớn.
Lời giải chi tiết
a) Ta có mẫu số liệu ghép nhóm với giá trị đại diện là: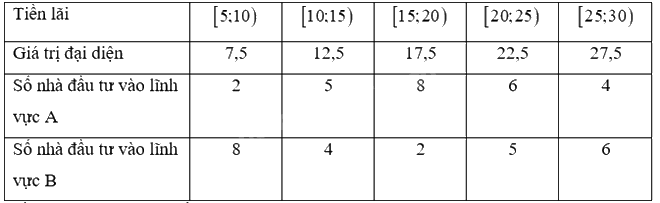
Tiền lãi trung bình khi đầu tư vào lĩnh vực A là:
\(\overline {{x_A}} = \frac{{7,5.2 + 12,5.5 + 17,5.8 + 22,5.6 + 27,5.4}}{{2 + 5 + 8 + 6 + 4}} = 18,5\) (triệu đồng)
Tiền lãi trung bình khi đầu tư vào lĩnh vực B là:
\(\overline {{x_B}} = \frac{{7,5.8 + 12,5.4 + 17,5.2 + 22,5.5 + 27,5.6}}{{8 + 4 + 2 + 5 + 6}} = 16,9\) (triệu đồng)
Do đó, về trung bình, đầu tư vào lĩnh vực A đem lại tiền lãi cao hơn.
b) Phương sai của mẫu số liệu về tiền lãi khi đầu tư vào lĩnh vực A:
\(s_A^2 = \frac{1}{{25}}\left( {7,{5^2}.2 + 12,{5^2}.5 + 17,{5^2}.8 + 22,{5^2}.6 + 27,{5^2}.4} \right) - 18,{5^2} = 34\)
Độ lệch chuẩn của mẫu số liệu về tiền lãi khi đầu tư vào lĩnh vực A: \({s_A} = \sqrt {34} \) (triệu đồng)
Phương sai của mẫu số liệu về tiền lãi khi đầu tư vào lĩnh vực B:
\(s_B^2 = \frac{1}{{25}}\left( {7,{5^2}.8 + 12,{5^2}.4 + 17,{5^2}.2 + 22,{5^2}.5 + 27,{5^2}.6} \right) - 16,{9^2} = 64,64\)
Độ lệch chuẩn của mẫu số liệu về tiền lãi khi đầu tư vào lĩnh vực B: \({s_B} = \sqrt {64,64} \) (triệu đồng)
Như vậy, độ lệch chuẩn của mẫu số liệu về tiền lãi đầu tư vào lĩnh vực B lớn hơn độ lệch chuẩn của mẫu số liệu về tiền lãi đầu tư vào lĩnh vực A nên đầu tư vào lĩnh vực B là rủi ro hơn.
Giải Bài Tập 3.15 Trang 86 Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 3.15 trang 86 SGK Toán 12 tập 1 Kết nối tri thức thuộc chương 1: Hàm số và đồ thị. Bài tập này thường liên quan đến việc xác định tính đơn điệu của hàm số, tìm cực trị, và vẽ đồ thị hàm số. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Phân tích đề bài và xác định yêu cầu
Trước khi bắt đầu giải, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, bài tập 3.15 sẽ yêu cầu:
- Xác định khoảng đồng biến, nghịch biến của hàm số.
- Tìm điểm cực đại, cực tiểu của hàm số.
- Vẽ đồ thị hàm số.
Phương pháp giải
Để giải bài tập này, chúng ta sẽ sử dụng các kiến thức về:
- Đạo hàm của hàm số.
- Điều kiện để hàm số đồng biến, nghịch biến.
- Điều kiện để hàm số có cực đại, cực tiểu.
Lời giải chi tiết bài tập 3.15 trang 86
(Giả sử bài tập 3.15 là hàm số y = x3 - 3x2 + 2)
- Tính đạo hàm cấp nhất: y' = 3x2 - 6x
- Tìm điểm dừng: Giải phương trình y' = 0, ta được x = 0 hoặc x = 2
- Xác định khoảng đồng biến, nghịch biến:
- Với x < 0, y' > 0 nên hàm số đồng biến trên (-∞, 0)
- Với 0 < x < 2, y' < 0 nên hàm số nghịch biến trên (0, 2)
- Với x > 2, y' > 0 nên hàm số đồng biến trên (2, +∞)
- Tìm cực trị:
- Tại x = 0, y' đổi dấu từ dương sang âm nên hàm số có cực đại tại x = 0, ycđ = 2
- Tại x = 2, y' đổi dấu từ âm sang dương nên hàm số có cực tiểu tại x = 2, yct = -2
- Vẽ đồ thị hàm số: Dựa vào các thông tin trên, ta có thể vẽ được đồ thị hàm số y = x3 - 3x2 + 2.
Lưu ý quan trọng
Khi giải bài tập về hàm số, cần chú ý:
- Kiểm tra kỹ điều kiện xác định của hàm số.
- Tính đạo hàm chính xác.
- Phân tích dấu của đạo hàm để xác định khoảng đồng biến, nghịch biến và cực trị.
- Vẽ đồ thị hàm số một cách chính xác.
Bài tập tương tự
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự trong SGK Toán 12 tập 1 Kết nối tri thức hoặc các đề thi thử Toán 12.
Kết luận
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể giải bài tập 3.15 trang 86 SGK Toán 12 tập 1 Kết nối tri thức một cách dễ dàng. Nếu bạn có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ.
| Khái niệm | Giải thích |
|---|---|
| Hàm số đồng biến | Hàm số y = f(x) được gọi là đồng biến trên khoảng (a, b) nếu với mọi x1, x2 thuộc (a, b) và x1 < x2 thì f(x1) < f(x2). |
| Hàm số nghịch biến | Hàm số y = f(x) được gọi là nghịch biến trên khoảng (a, b) nếu với mọi x1, x2 thuộc (a, b) và x1 < x2 thì f(x1) > f(x2). |