Đề bài
Nghệ thuật làm gốm có lịch sử phát triển lâu đời và vẫn còn tồn tại cho đến ngày nay. Giả sử một bình gốm có mặt trong bình là một mặt tròn xoay sinh ra khi cho phần đồ thị của hàm số \(y = \frac{1}{{175}}{x^2} + \frac{3}{{35}}x + 5\left( {0 \le x \le 30} \right)\) (x, y tính theo cm) quay tròn quanh bệ gồm có trục trùng với trục hoành Ox. Hỏi để hoàn thành bình gốm đó ta cần sử dụng bao nhiêu \(c{m^3}\) đất sét, biết rằng bình gốm đó có độ dày không đổi là 1 cm.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về công thức tính thể tích của khối tròn xoay để tính: Cho hàm số f(x) liên tục, không âm trên đoạn [a; b]. Khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\) xung quanh trục hoành, ta được hình khối gọi là một khối tròn xoay. Khi cắt khối tròn xoay đó bởi một mặt phẳng vuông góc với trục Ox tại điểm \(x \in \left[ {a;b} \right]\) được một hình tròn có bán kính f(x). Thể tích của khối tròn xoay này là: \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \).
Lời giải chi tiết
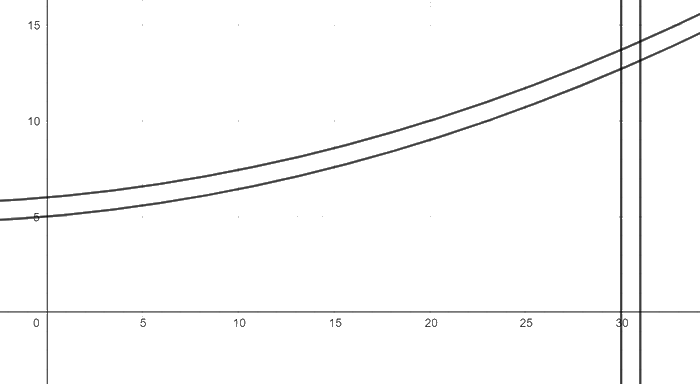
Gọi \(f(x) = \frac{1}{{175}}{x^2} + \frac{3}{{35}}x + 5\) là đồ thị mặt trong của thành bình.
Khi đó, \(g(x) = f(x) + 1 = \frac{1}{{175}}{x^2} + \frac{3}{{35}}x + 6\) là đồ thị mặt ngoài của thành bình (vì độ dày của bình là 1 cm).
Gọi \({V_N}\) là thể tích bình kể cả vỏ bình, \({V_T}\) là thể tích phần rỗng trong bình.
Khi đó, thể tích đất sét để làm bình gốm là \(V = {V_N} - {V_T}\).
\({V_T}\) được giới hạn bởi đồ thị \(f(x) = \frac{1}{{175}}{x^2} + \frac{3}{{35}}x + 5\), trục hoành và hai đường thẳng x = 0, x = 30.
Ta có \({V_T} = \pi \int\limits_0^{30} {{{\left( {\frac{1}{{175}}{x^2} + \frac{3}{{35}}x + 5} \right)}^2}dx} \approx 6513\) \((c{m^3})\).
\({V_N}\) được giới hạn bởi đồ thị \(g(x) = \frac{1}{{175}}{x^2} + \frac{3}{{35}}x + 6\), trục hoành và hai đường thẳng x = 0, x = 31 (do đáy bình cũng dày 1 cm).
Ta có \({V_N} = \pi \int\limits_0^{31} {{{\left( {\frac{1}{{175}}{x^2} + \frac{3}{{35}}x + 6} \right)}^2}dx} \approx 8725\) \((c{m^3})\).
Vậy thể tích đất sét để làm bình gốm là \(V = {V_N} - {V_T} \approx 8725 - 6513 = 2212\) \((c{m^3})\).
