Giải mục 1 trang 20, 21 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 1 trang 20, 21 SGK Toán 12 tập 1 - Kết nối tri thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 12 tập 1 - Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tốt nhất để giúp bạn học tập hiệu quả.
Bài viết này sẽ tập trung vào việc giải mục 1 trang 20, 21, giúp bạn hiểu rõ các khái niệm và phương pháp giải bài tập liên quan.
Đường tiệm cận ngang
LT1
Trả lời câu hỏi Luyện tập 1 trang 21 SGK Toán 12 Kết nối tri thức
Tìm tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x - 1}}{{x - 1}}\).
Phương pháp giải:
Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\).
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2x - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 - \frac{1}{x}}}{{1 - \frac{1}{x}}} = 2;\mathop {\lim }\limits_{x \to - \infty } \frac{{2x - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{2 - \frac{1}{x}}}{{1 - \frac{1}{x}}} = 2\).
Do đó, tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x - 1}}{{x - 1}}\) là \(y = 2\).
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 20 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{x}\) có đồ thị (C). Với \(x > 0\), xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng \(y = 2\) (H.1.19).
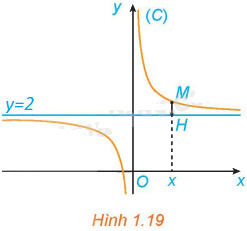
a) Tính khoảng cách MH.
b) Có nhận xét gì về khoảng cách MH khi \(x \to + \infty \)?
Phương pháp giải:
Sử dụng kiến thức về giới hạn của hàm số để tính.
Lời giải chi tiết:
a) Ta có: \(M\left( {x;\frac{{2x + 1}}{x}} \right)\); \(H\left( {x;2} \right)\).
Do đó, \(MH = \sqrt {{{\left( {x - x} \right)}^2} + {{\left( {2 - \frac{{2x + 1}}{x}} \right)}^2}} = \sqrt {{{\left( {\frac{{2x - 2x - 1}}{x}} \right)}^2}} = \frac{1}{x}\) (do \(x > 0\))
b) Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 0\). Do đó, khi \(x \to + \infty \) thì \(MH \to 0\).
VD1
Trả lời câu hỏi Vận dụng 1 trang 21 SGK Toán 12 Kết nối tri thức
Giải bài toán trong tình huống mở đầu.
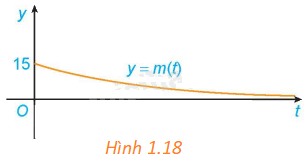
Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau t ngày phân rã được cho bởi hàm số \(m\left( t \right) = 15{e^{ - 0,012t}}\). Khối lượng m(t) thay đổi ra sao khi \(t \to + \infty \)? Điều này thể hiện trên Hình 1.18 như thế nào?
Phương pháp giải:
Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\).
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{t \to + \infty } m\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } 15{e^{ - 0,012t}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{15}}{{{e^{0,012t}}}} = 0\)
Do đó, \(m\left( t \right) \to 0\) khi \(t \to + \infty \).
Trong hình 1.18, khi \(t \to + \infty \) thì m(t) càng gần trục hoành Ot (nhưng không chạm trục Ot).
- HĐ1
- LT1
- VD1
Trả lời câu hỏi Hoạt động 1 trang 20 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{x}\) có đồ thị (C). Với \(x > 0\), xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng \(y = 2\) (H.1.19).
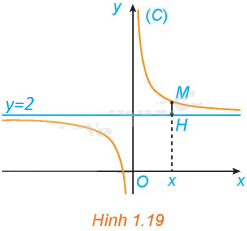
a) Tính khoảng cách MH.
b) Có nhận xét gì về khoảng cách MH khi \(x \to + \infty \)?
Phương pháp giải:
Sử dụng kiến thức về giới hạn của hàm số để tính.
Lời giải chi tiết:
a) Ta có: \(M\left( {x;\frac{{2x + 1}}{x}} \right)\); \(H\left( {x;2} \right)\).
Do đó, \(MH = \sqrt {{{\left( {x - x} \right)}^2} + {{\left( {2 - \frac{{2x + 1}}{x}} \right)}^2}} = \sqrt {{{\left( {\frac{{2x - 2x - 1}}{x}} \right)}^2}} = \frac{1}{x}\) (do \(x > 0\))
b) Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 0\). Do đó, khi \(x \to + \infty \) thì \(MH \to 0\).
Trả lời câu hỏi Luyện tập 1 trang 21 SGK Toán 12 Kết nối tri thức
Tìm tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x - 1}}{{x - 1}}\).
Phương pháp giải:
Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\).
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2x - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 - \frac{1}{x}}}{{1 - \frac{1}{x}}} = 2;\mathop {\lim }\limits_{x \to - \infty } \frac{{2x - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{2 - \frac{1}{x}}}{{1 - \frac{1}{x}}} = 2\).
Do đó, tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x - 1}}{{x - 1}}\) là \(y = 2\).
Trả lời câu hỏi Vận dụng 1 trang 21 SGK Toán 12 Kết nối tri thức
Giải bài toán trong tình huống mở đầu.
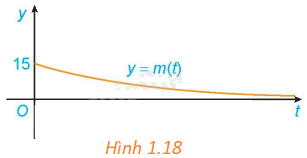
Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau t ngày phân rã được cho bởi hàm số \(m\left( t \right) = 15{e^{ - 0,012t}}\). Khối lượng m(t) thay đổi ra sao khi \(t \to + \infty \)? Điều này thể hiện trên Hình 1.18 như thế nào?
Phương pháp giải:
Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\).
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{t \to + \infty } m\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } 15{e^{ - 0,012t}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{15}}{{{e^{0,012t}}}} = 0\)
Do đó, \(m\left( t \right) \to 0\) khi \(t \to + \infty \).
Trong hình 1.18, khi \(t \to + \infty \) thì m(t) càng gần trục hoành Ot (nhưng không chạm trục Ot).
Giải mục 1 trang 20, 21 SGK Toán 12 tập 1 - Kết nối tri thức: Tổng quan và Phương pháp
Mục 1 của chương trình Toán 12 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và mở rộng kiến thức về hàm số và đồ thị. Đây là nền tảng quan trọng cho các chương tiếp theo, vì vậy việc nắm vững kiến thức ở mục này là vô cùng cần thiết.
Nội dung chính của Mục 1
- Ôn tập về hàm số: Khái niệm hàm số, tập xác định, tập giá trị, tính đơn điệu, cực trị của hàm số.
- Đồ thị hàm số: Cách vẽ đồ thị hàm số, các phép biến hình đồ thị.
- Hàm số bậc hai: Phương trình bậc hai, đồ thị parabol, ứng dụng của hàm số bậc hai.
- Hàm số mũ và hàm số logarit: Khái niệm, tính chất, đồ thị và ứng dụng.
Giải chi tiết các bài tập trang 20, 21
Bài 1: (Trang 20)
Bài 1 yêu cầu xác định tập xác định của hàm số. Để giải bài này, bạn cần nhớ lại điều kiện xác định của các hàm số cơ bản như phân thức, căn bậc hai, logarit. Ví dụ, nếu hàm số có chứa phân thức \frac{1}{x-2}, thì tập xác định là \mathbb{R} \setminus \{2\}.
Bài 2: (Trang 20)
Bài 2 thường liên quan đến việc xét tính đơn điệu của hàm số. Bạn có thể sử dụng đạo hàm để xác định dấu của đạo hàm trên các khoảng xác định, từ đó kết luận về tính đơn điệu của hàm số.
Bài 3: (Trang 21)
Bài 3 có thể yêu cầu vẽ đồ thị hàm số. Để vẽ đồ thị, bạn cần xác định các yếu tố quan trọng như điểm cực trị, điểm uốn, giao điểm với các trục tọa độ. Sau đó, bạn có thể vẽ đồ thị bằng cách nối các điểm này lại với nhau.
Bài 4: (Trang 21)
Bài 4 thường là bài toán ứng dụng của hàm số, ví dụ như tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước. Bạn có thể sử dụng các phương pháp như phương pháp đổi biến, phương pháp đánh giá để giải bài toán này.
Mẹo học tập hiệu quả
- Nắm vững lý thuyết: Trước khi bắt tay vào giải bài tập, hãy đảm bảo bạn đã hiểu rõ các khái niệm và định lý liên quan.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập.
- Sử dụng tài liệu tham khảo: Tham khảo thêm các sách giáo khoa, tài liệu ôn tập, bài giảng trực tuyến để mở rộng kiến thức.
- Hỏi thầy cô, bạn bè: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô, bạn bè để được giúp đỡ.
Bảng tổng hợp các công thức quan trọng
| Công thức | Mô tả |
|---|---|
| Đạo hàm của hàm số y = f(x) | y' = f'(x) |
| Hàm số bậc hai y = ax^2 + bx + c | Đỉnh của parabol: (-\frac{b}{2a}, \frac{-b^2 + 4ac}{4a}) |
Hy vọng với những giải thích chi tiết và hướng dẫn cụ thể trên, bạn sẽ tự tin hơn trong việc giải các bài tập mục 1 trang 20, 21 SGK Toán 12 tập 1 - Kết nối tri thức. Chúc bạn học tập tốt!