1. Công thức xác suất toàn phần
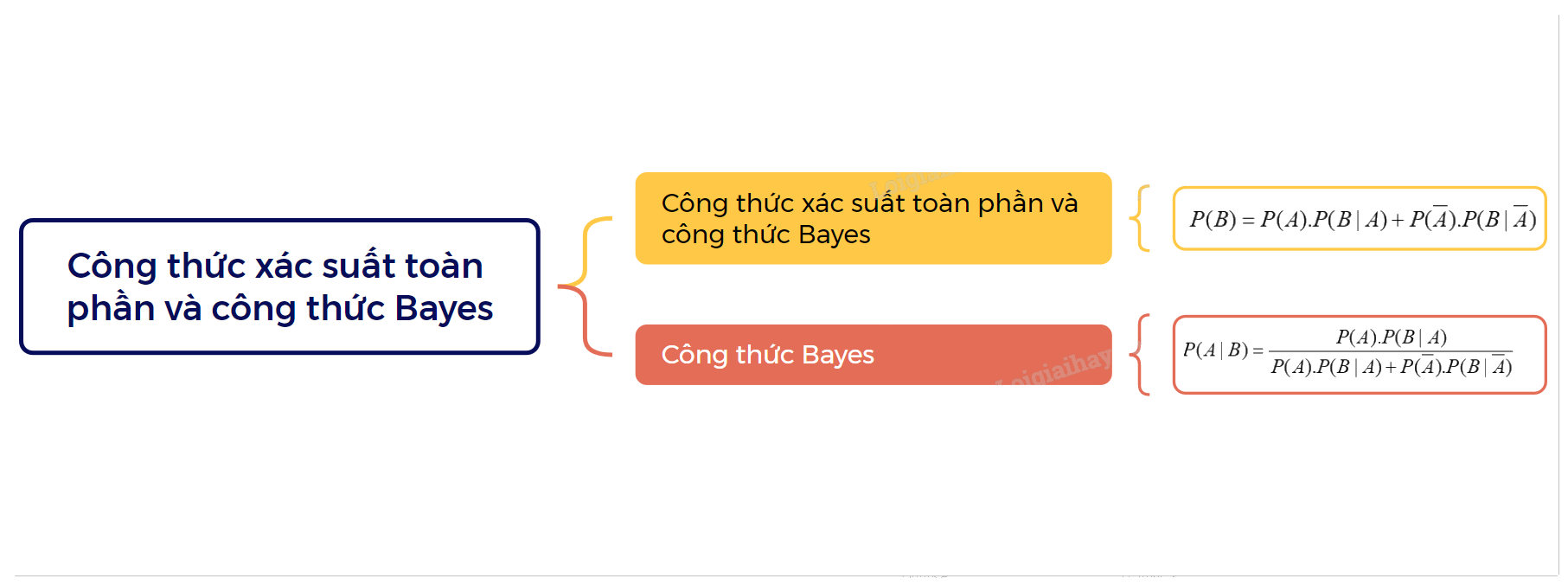
Cho hai biến cố A và B. Khi đó, ta có công thức sau: \(P(B) = P(A).P(B|A) + P(\overline A ).P(B|\overline A )\) |
Ví dụ 1: Ông An hằng ngày đi làm bằng xe máy hoặc xe buýt. Nếu hôm nay ông đi làm bằng xe buýt thì xác suất để hôm sau ông đi làm bằng xe máy là 0,4. Nếu hôm nay ông đi làm bằng xe máy thì xác suất để hôm sau ông đi làm bằng xe buýt là 0,7. Xét một tuần mà thứ hai ông An đi làm bằng xe buýt. Tính xác suất để thứ tư trong tuần đó, ông An đi làm bằng xe máy.
Giải:
Gọi A là biến cố: “Thứ ba, ông An đi làm bằng xe máy”; B là biến cố: “Thứ tư, ông An đi làm bằng xe máy”. Ta cần tính P(B). Theo công thức xác suất toàn phần, ta có:
\(P(B) = P(A).P(B|A) + P(\overline A ).P(B|\overline A )\)
- Tính P(A): Vì thứ hai, ông An đi làm bằng xe buýt nên xác suất để thứ ba ông đi làm bằng xe máy là 0,4. Vậy P(A) = 0,4.
- Tính \(P(\overline A )\): Ta có \(P(\overline A )\) = 1 – 0,4 = 0,6.
- Tính P(B|A): Đây là xác suất để thứ tư ông An đi làm bằng xe máy nếu thứ ba ông An đi làm bằng xe máy.
- Theo giả thiết, nếu hôm nay ông đi làm bằng xe máy thì xác suất để hôm sau ông đi làm bằng xe buýt là 0,7 và đi làm bằng xe máy là 0,3. Do đó, nếu thứ ba ông An đi làm bằng xe máy thì xác suất để thứ tư, ông đi làm bằng xe máy là 0,3. Vậy P(B|A) = 0,3.
- Tính \(P(B|\overline A )\): Đây là xác suất để thứ tư ông An đi làm bằng xe máy nếu thứ ba ông An đi làm bằng xe buýt. Theo giả thiết, nếu hôm nay ông đi làm bằng xe buýt thì xác suất để hôm sau ông đi làm bằng xe máy là 0,4. Do đó, nếu thứ ba ông An đi làm bằng xe buýt thì xác suất để thứ tư ông đi làm bằng xe máy là 0,4. Suy ra \(P(B|\overline A )\). Vậy:
\(P(B) = P(A).P(B|A) + P(\overline A ).P(B|\overline A ) = 0,4.0,3 + 0,6.0,4 = 0,36\)
2. Công thức Bayes
Cho A và B là hai biến cố, với P(B) > 0. Khi đó, ta có công thức sau: \(P(A|B) = \frac{{P(A).P(B|A)}}{{P(A).P(B|A) + P(\overline A ).P(B|\overline A )}}\) |
Ví dụ 2: Trong một kỳ thi tốt nghiệp trung học phổ thông, một tỉnh X có 80% học sinh lựa chọn tổ hợp A00. Biết rằng, nếu một học sinh chọn tổ hợp A00 thì xác suất để học sinh đó đỗ đại học là 0,6; còn nếu mọt học sinh không chọn tổ hợp A00 thì xác suất để học sinh đỗ đại học là 0,7. Chọn ngẫu nhiên một học sinh của tỉnh X đã tốt nghiệp trung học phổ thông trong kì thi trên. Biết rằng học sinh này đã đỗ đại học. Tính xác suất để học sinh đó chọn tổ hợp A00.
Giải:
Gọi A là biến cố: “Học sinh đó chọn tổ hợp A00”; B là biến cố: “Học sinh đó đỗ đại học”.
Ta cần tính P(A|B). Theo công thức Bayes, ta cần biết: \(P(A),P(\overline A ),P(B|A)\) và \(P(B|\overline A )\).
Ta có: P(A) = 0,8; \(P(\overline A )\) = 1 – P(A) = 1 – 0,8 = 0,2.
P(B|A) là xác suất để một học sinh đỗ đại học với điều kiện học sinh đó chọn tổ hợp A00.
\( \Rightarrow P(B|A) = 0,6\).
\(P(B|\overline A )\) là xác suất để một học sinh đỗ đại học với điều kiện học sinh đó không chọn tổ hợp A00.
\( \Rightarrow P(B|\overline A ) = 0,7\).
Thay vào công thức Bayes ta được:
\(P(A|B) = \frac{{P(A).P(B|A)}}{{P(A).P(B|A) + P(\overline A ).P(B|\overline A )}} = \frac{{0,8.0,6}}{{0,8.0,6 + 0,2.0,7}} \approx 0,7742\)
