Giải bài tập 2.4 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 2.4 Trang 58 Toán 12 Tập 1 - Kết Nối Tri Thức
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 2.4 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức trên tusach.vn. Bài viết này sẽ giúp các em hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và hữu ích nhất cho các em trong quá trình học tập.
Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng: a) \(\overrightarrow {AB} + \overrightarrow {DD'} + \overrightarrow {C'D'} = \overrightarrow {CC'} \); b) \(\overrightarrow {AB} + \overrightarrow {CD'} - \overrightarrow {CC'} = \overrightarrow 0 \); c) \(\overrightarrow {BC} - \overrightarrow {CC'} + \overrightarrow {DC} = \overrightarrow {A'C} \)
Đề bài
Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng:a) \(\overrightarrow {AB} + \overrightarrow {DD'} + \overrightarrow {C'D'} = \overrightarrow {CC'} \);b) \(\overrightarrow {AB} + \overrightarrow {CD'} - \overrightarrow {CC'} = \overrightarrow 0 \);c) \(\overrightarrow {BC} - \overrightarrow {CC'} + \overrightarrow {DC} = \overrightarrow {A'C} \)
Phương pháp giải - Xem chi tiết
a, b) Sử dụng kiến thức về quy tắc ba điểm để chứng minh: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
c) Sử dụng quy tắc hình bình hành để chứng minh: Nếu ABCD là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Lời giải chi tiết
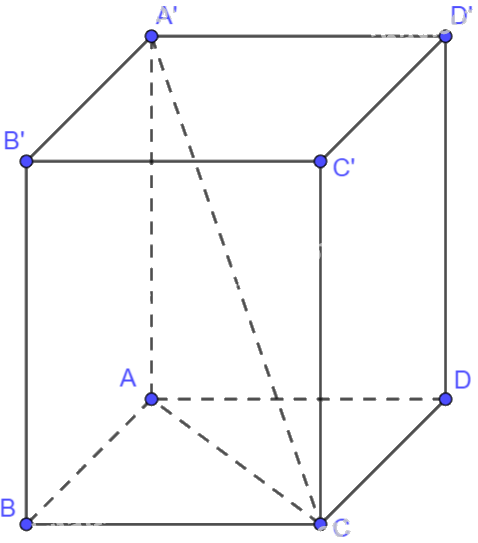
a) Vì ABCD là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \)
Vì CDD’C’ là hình bình hành nên \(\overrightarrow {C'D'} = \overrightarrow {CD} ,\overrightarrow {DD'} = \overrightarrow {CC'} \)
Ta có: \(\overrightarrow {AB} + \overrightarrow {DD'} + \overrightarrow {C'D'} = \overrightarrow {DC} + \overrightarrow {CC'} + \overrightarrow {CD} = \left( {\overrightarrow {CD} + \overrightarrow {DC} } \right) + \overrightarrow {CC'} = \overrightarrow {CC'} \)
b) Ta có: \(\overrightarrow {AB} + \overrightarrow {CD'} - \overrightarrow {CC'} = \overrightarrow {AB} + \overrightarrow {C'D'} = \overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow 0 \)
c) Vì ABCD là hình bình hành nên \(\overrightarrow {CB} + \overrightarrow {CD} = \overrightarrow {CA} \)
Vì A’ACC’ là hình bình hành nên \(\overrightarrow {CA} + \overrightarrow {CC'} = \overrightarrow {CA'} \)
\(\overrightarrow {BC} - \overrightarrow {CC'} + \overrightarrow {DC} = - \left( {\overrightarrow {CB} + \overrightarrow {CD} } \right) - \overrightarrow {CC'} = - \overrightarrow {CA} - \overrightarrow {CC'} = - \left( {\overrightarrow {CA} + \overrightarrow {CC'} } \right) = - \overrightarrow {CA'} = \overrightarrow {A'C} \)
Giải Bài Tập 2.4 Trang 58 Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 2.4 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập 2.4 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức
Bài tập yêu cầu tính đạo hàm của các hàm số sau:
- a) y = x3 - 3x2 + 2
- b) y = 2x4 + 5x - 1
- c) y = (x2 + 1)(x - 2)
- d) y = (x2 + 3x)(x2 - x + 1)
Lời giải chi tiết
Để giải bài tập này, chúng ta cần nắm vững các quy tắc tính đạo hàm cơ bản:
- Đạo hàm của hàm số lũy thừa: (xn)' = nxn-1
- Đạo hàm của tổng/hiệu: (u ± v)' = u' ± v'
- Quy tắc nhân: (uv)' = u'v + uv'
a) Giải y = x3 - 3x2 + 2
y' = (x3)' - 3(x2)' + (2)' = 3x2 - 6x + 0 = 3x2 - 6x
b) Giải y = 2x4 + 5x - 1
y' = 2(x4)' + 5(x)' - (1)' = 8x3 + 5 - 0 = 8x3 + 5
c) Giải y = (x2 + 1)(x - 2)
Áp dụng quy tắc nhân: y' = (x2 + 1)'(x - 2) + (x2 + 1)(x - 2)' = (2x)(x - 2) + (x2 + 1)(1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1
d) Giải y = (x2 + 3x)(x2 - x + 1)
Áp dụng quy tắc nhân: y' = (x2 + 3x)'(x2 - x + 1) + (x2 + 3x)(x2 - x + 1)' = (2x + 3)(x2 - x + 1) + (x2 + 3x)(2x - 1) = (2x3 - 2x2 + 2x + 3x2 - 3x + 3) + (2x3 - x2 + 6x2 - 3x) = 2x3 + x2 - x + 3 + 2x3 + 5x2 - 3x = 4x3 + 6x2 - 4x + 3
Lưu ý khi giải bài tập về đạo hàm
- Nắm vững các quy tắc tính đạo hàm cơ bản.
- Áp dụng đúng quy tắc khi tính đạo hàm của các hàm số phức tạp.
- Kiểm tra lại kết quả sau khi tính toán.
Tổng kết
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập 2.4 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức trên tusach.vn, các em đã hiểu rõ cách giải bài tập này và có thể tự tin áp dụng vào các bài tập tương tự. Chúc các em học tập tốt!
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ.