Giải bài tập 1.10 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 1.10 Trang 19 Toán 12 Tập 1 - Kết Nối Tri Thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 12 tập 1 - Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn giải bài tập 1.10 trang 19 một cách dễ hiểu nhất.
Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) (y = - {x^2} + 4x + 3); b) (y = {x^3} - 2{x^2} + 1) trên (left[ {0; + infty } right)); c) (y = frac{{{x^2} - 2x + 3}}{{x - 1}}) trên (left( {1; + infty } right)); d) (y = sqrt {4x - 2{x^2}} ).
Đề bài
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:a) \(y = - {x^2} + 4x + 3\);b) \(y = {x^3} - 2{x^2} + 1\) trên \(\left[ {0; + \infty } \right)\);c) \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\) trên \(\left( {1; + \infty } \right)\);d) \(y = \sqrt {4x - 2{x^2}} \).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về cách tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn để tính: Giả sử \(y = f\left( x \right)\) là hàm số liên tục trên \(\left[ {a;b} \right]\) và có đạo hàm trên (a; b), có thể trừ ra tại một số hữu hạn điểm mà tại đó hàm số không có đạo hàm. Giả sử chỉ có hữu hạn điểm trong đoạn \(\left[ {a;b} \right]\) mà đạo hàm \(f'\left( x \right) = 0\).
Các bước tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {a;b} \right]\):
1. Tìm các điểm \({x_1},{x_2},...{x_n} \in \left( {a;b} \right)\), tại đó \(f'\left( x \right) = 0\) hoặc không tồn tại.
2. Tính \(f\left( {{x_1}} \right);f\left( {{x_2}} \right);...;f\left( {{x_n}} \right)\), f(a) và f(b).
3. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:
\(M = \mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right),m = \mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right)\)
Lời giải chi tiết
a) Ta có: \(y = - {x^2} + 4x + 3 \), khi đó \(y' = - 2x + 4 = 0 \Leftrightarrow x = 2\).
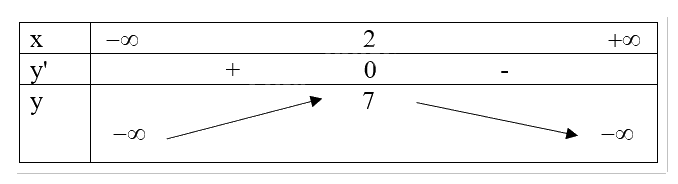
Do đó, \(\max f\left( x \right) = f\left( 2 \right) = 7\), hàm số không có giá trị nhỏ nhất.
b) GTLN, GTNN của \(y = {x^3} - 2{x^2} + 1\) trên \(\left[ {0; + \infty } \right)\).
Ta có: \(y' = 3{x^2} - 4x,y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\left( {tm} \right)\\x = \frac{4}{3}\left( {tm} \right)\end{array} \right.\)
Bảng biến thiên:
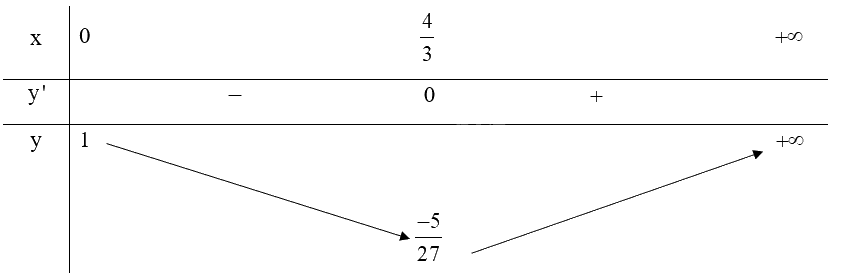
Do đó, \(\mathop {\min }\limits_{\left[ {0; + \infty } \right)} y = y\left( {\frac{4}{3}} \right) = \frac{{ - 5}}{{27}}\), hàm số không có giá trị lớn nhất.
c) Ta có: \(y' = \frac{{\left( {2x - 2} \right)\left( {x - 1} \right) - \left( {{x^2} - 2x + 3} \right)}}{{{{\left( {x - 1} \right)}^2}}} = \frac{{{x^2} - 2x - 1}}{{{{\left( {x - 1} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow x = 1 + \sqrt 2 \) (do \(x \in \left( {1; + \infty } \right)\))
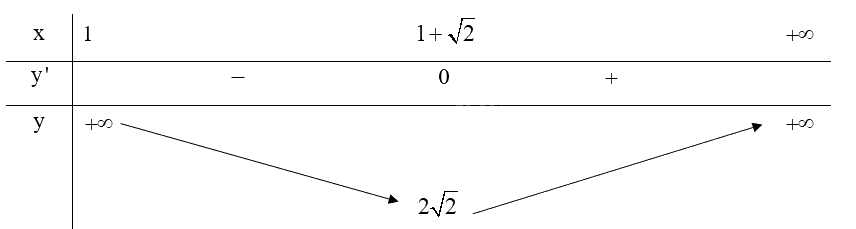
Do đó, \(\mathop {\min }\limits_{\left( {1; + \infty } \right)} y = y\left( {1 + \sqrt 2 } \right) = 2\sqrt 2 \), hàm số không có giá trị lớn nhất trên \(\left( {1; + \infty } \right)\).
d) Tập xác định của hàm số là: \(D = \left[ {0;2} \right]\)
\(y' = \frac{{\left( {4x - 2{x^2}} \right)'}}{{2\sqrt {4x - 2{x^2}} }} = \frac{{4 - 4x}}{{2\sqrt {4x - 2{x^2}} }} = \frac{{2\left( {1 - x} \right)}}{{\sqrt {4x - 2{x^2}} }}\)
\(y' = 0 \Leftrightarrow x = 1\left( {tm} \right)\)
\(y\left( 0 \right) = 0;y\left( 1 \right) = \sqrt 2 ;y\left( 2 \right) = 0\).
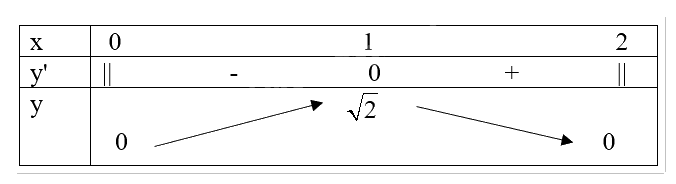
Do đó, \(\mathop {\max }\limits_{\left[ {0;2} \right]} y = y\left( 1 \right) = \sqrt 2 ,\mathop {\min }\limits_{\left[ {0;2} \right]} y = y\left( 0 \right) = y\left( 2 \right) = 0\).
Giải Bài Tập 1.10 Trang 19 Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 1.10 trang 19 SGK Toán 12 tập 1 Kết nối tri thức thuộc chương 1: Hàm số và đồ thị. Bài tập này thường liên quan đến việc xác định tính đơn điệu của hàm số, tìm khoảng đồng biến, nghịch biến và cực trị của hàm số. Để giải bài tập này một cách hiệu quả, bạn cần nắm vững các kiến thức cơ bản về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
I. Đề Bài Bài Tập 1.10 Trang 19 Toán 12 Tập 1 - Kết Nối Tri Thức
(Đề bài cụ thể của bài tập 1.10 sẽ được chèn vào đây. Ví dụ: Cho hàm số y = f(x) = x3 - 3x2 + 2. Hãy tìm khoảng đồng biến, nghịch biến và cực trị của hàm số.)
II. Phương Pháp Giải Bài Tập Khảo Sát Hàm Số
Để giải quyết bài tập 1.10 trang 19, chúng ta sẽ thực hiện theo các bước sau:
- Xác định tập xác định của hàm số: Tìm khoảng mà hàm số có nghĩa.
- Tính đạo hàm cấp nhất f'(x): Đạo hàm cấp nhất đóng vai trò quan trọng trong việc xác định tính đơn điệu của hàm số.
- Tìm các điểm tới hạn: Giải phương trình f'(x) = 0 để tìm các điểm mà đạo hàm bằng 0.
- Lập bảng biến thiên: Dựa vào dấu của đạo hàm cấp nhất trên các khoảng xác định, ta có thể xác định khoảng đồng biến, nghịch biến của hàm số.
- Xác định cực trị: Sử dụng dấu của đạo hàm cấp nhất để xác định điểm cực đại, cực tiểu của hàm số.
III. Lời Giải Chi Tiết Bài Tập 1.10 Trang 19 Toán 12 Tập 1 - Kết Nối Tri Thức
(Lời giải chi tiết của bài tập 1.10 sẽ được trình bày ở đây, bao gồm các bước tính toán, giải thích và kết luận. Ví dụ:
Bước 1: Tập xác định của hàm số y = x3 - 3x2 + 2 là D = ℝ.
Bước 2: Đạo hàm cấp nhất của hàm số là f'(x) = 3x2 - 6x.
Bước 3: Giải phương trình f'(x) = 0, ta được 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2.
Bước 4: Lập bảng biến thiên:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Bước 5: Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2). Hàm số đạt cực đại tại x = 0 với giá trị f(0) = 2 và đạt cực tiểu tại x = 2 với giá trị f(2) = -2.
)
IV. Lưu Ý Khi Giải Bài Tập Khảo Sát Hàm Số
- Luôn kiểm tra lại tập xác định của hàm số.
- Tính đạo hàm chính xác và cẩn thận.
- Lập bảng biến thiên một cách khoa học và rõ ràng.
- Kết luận chính xác về tính đơn điệu, cực trị và các điểm đặc biệt của hàm số.
V. Bài Tập Tương Tự
Để củng cố kiến thức, bạn có thể tham khảo thêm các bài tập tương tự sau:
- Bài tập 1.11 trang 19 SGK Toán 12 tập 1 Kết nối tri thức
- Bài tập 1.12 trang 20 SGK Toán 12 tập 1 Kết nối tri thức
Hy vọng bài viết này đã giúp bạn hiểu rõ cách giải bài tập 1.10 trang 19 SGK Toán 12 tập 1 Kết nối tri thức. Chúc bạn học tập tốt!