Giải mục 5 trang 37,38 SGK Toán 12 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải mục 5 trang 37,38 SGK Toán 12 tập 2 - Kết nối tri thức
Chào mừng bạn đến với lời giải chi tiết mục 5 trang 37,38 SGK Toán 12 tập 2 - Kết nối tri thức trên tusach.vn. Chúng tôi hiểu rằng việc tự học và làm bài tập có thể gặp nhiều khó khăn. Do đó, chúng tôi đã biên soạn lời giải này một cách cẩn thận, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài giải này bao gồm các bước thực hiện chi tiết, giải thích rõ ràng từng bước, giúp bạn hiểu được bản chất của bài toán.
ĐIỀU KIỆN ĐỂ HAI MẶT PHẲNG SONG SONG VỚI NHAU
LT10
Trả lời câu hỏi Luyện tập 10 trang 37 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai mặt phẳng: \(\left( \alpha \right):5x + 2y - 4z + 6 = 0\) và \(\left( \beta \right):10x + 4y - 2z + 12 = 0\)
a) Hỏi \(\left( \alpha \right)\) và \(\left( \beta \right)\) có song song với nhau hay không?
b) Chứng minh rằng điểm \(M\left( {1; - 3;5} \right)\) không thuộc mặt phẳng \(\left( \alpha \right)\) nhưng thuộc mặt phẳng \(\left( \beta \right)\).
c) Viết phương trình mặt phẳng (P) đi qua \(M\left( {1; - 3;5} \right)\) và song song với \(\left( \alpha \right)\).
Phương pháp giải:
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song hoặc trùng nhau để tính: Trong không gian Oxyz, cho hai mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\), \(\left( \beta \right):A'x + B'y + C'z + D' = 0\) với các vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\) tương ứng. Khi đó, \(\left( \alpha \right)//\left( \beta \right) \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {n'} = k\overrightarrow n \\D' \ne kD\end{array} \right.\) với k nào đó.
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để tính: Nếu hai mặt phẳng song song với nhau thì vectơ pháp tuyến của mặt phẳng này cũng là vectơ pháp tuyến của mặt phẳng kia.
Lời giải chi tiết:
a) Mặt phẳng \(\left( \alpha \right)\) có một vectơ pháp tuyến là: \(\overrightarrow {{n_\alpha }} = \left( {5;2; - 4} \right)\), mặt phẳng \(\left( \beta \right)\) có một vectơ pháp tuyến là: \(\overrightarrow {{n_\beta }} = \left( {10;4; - 2} \right)\).
Vì \(\frac{5}{{10}} = \frac{4}{2} \ne \frac{{ - 4}}{2}\) nên \(\overrightarrow {{n_\alpha }} \) và \(\overrightarrow {{n_\beta }} \) không cùng phương. Do đó, hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) không song song với nhau.
b) Vì \(5.1 - 3.2 - 4.5 + 6 = 5 - 6 - 20 + 6 = - 15 \ne 0\) nên điểm \(M\left( {1; - 3;5} \right)\) không thuộc mặt phẳng \(\left( \alpha \right)\).
Vì \(10.1 + 4.\left( { - 3} \right) - 2.5 + 12 = 0\) nên điểm \(M\left( {1; - 3;5} \right)\) thuộc mặt phẳng \(\left( \beta \right)\).
c) Vì mặt phẳng (P) song song với \(\left( \alpha \right)\) nên mặt phẳng (P) nhận \(\overrightarrow {{n_\alpha }} = \left( {5;2; - 4} \right)\) làm một vectơ pháp tuyến. Mà điểm \(M\left( {1; - 3;5} \right)\) thuộc (P) nên phương trình mặt phẳng (P) là:
\(5\left( {x - 1} \right) + 2\left( {y + 3} \right) - 4\left( {z - 5} \right) = 0 \Leftrightarrow 5x + 2y - 4z + 21 = 0\)
HĐ9
Trả lời câu hỏi Hoạt động 9 trang 37 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\), \(\left( \beta \right):A'x + B'y + C'z + D' = 0\) với các vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\) tương ứng.
Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song hoặc trùng nhau thì các vectơ \(\overrightarrow n ,\overrightarrow {n'} \) có mối quan hệ gì?
Phương pháp giải:
Sử dụng kiến thức về vectơ pháp tuyến của mặt phẳng: Vectơ \(\overrightarrow n \ne \overrightarrow 0 \) được gọi là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) nếu \(\overrightarrow n \) vuông góc với \(\left( \alpha \right)\).
Lời giải chi tiết:
Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song hoặc trùng nhau thì giá của các vectơ \(\overrightarrow n ,\overrightarrow {n'} \) song song song hoặc trùng nhau. Do đó, các vectơ \(\overrightarrow n ,\overrightarrow {n'} \) cùng phương với nhau.
- HĐ9
- LT10
- VD4
Trả lời câu hỏi Hoạt động 9 trang 37 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\), \(\left( \beta \right):A'x + B'y + C'z + D' = 0\) với các vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\) tương ứng.
Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song hoặc trùng nhau thì các vectơ \(\overrightarrow n ,\overrightarrow {n'} \) có mối quan hệ gì?
Phương pháp giải:
Sử dụng kiến thức về vectơ pháp tuyến của mặt phẳng: Vectơ \(\overrightarrow n \ne \overrightarrow 0 \) được gọi là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) nếu \(\overrightarrow n \) vuông góc với \(\left( \alpha \right)\).
Lời giải chi tiết:
Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song hoặc trùng nhau thì giá của các vectơ \(\overrightarrow n ,\overrightarrow {n'} \) song song song hoặc trùng nhau. Do đó, các vectơ \(\overrightarrow n ,\overrightarrow {n'} \) cùng phương với nhau.
Trả lời câu hỏi Luyện tập 10 trang 37 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai mặt phẳng: \(\left( \alpha \right):5x + 2y - 4z + 6 = 0\) và \(\left( \beta \right):10x + 4y - 2z + 12 = 0\)
a) Hỏi \(\left( \alpha \right)\) và \(\left( \beta \right)\) có song song với nhau hay không?
b) Chứng minh rằng điểm \(M\left( {1; - 3;5} \right)\) không thuộc mặt phẳng \(\left( \alpha \right)\) nhưng thuộc mặt phẳng \(\left( \beta \right)\).
c) Viết phương trình mặt phẳng (P) đi qua \(M\left( {1; - 3;5} \right)\) và song song với \(\left( \alpha \right)\).
Phương pháp giải:
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song hoặc trùng nhau để tính: Trong không gian Oxyz, cho hai mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\), \(\left( \beta \right):A'x + B'y + C'z + D' = 0\) với các vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\) tương ứng. Khi đó, \(\left( \alpha \right)//\left( \beta \right) \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {n'} = k\overrightarrow n \\D' \ne kD\end{array} \right.\) với k nào đó.
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để tính: Nếu hai mặt phẳng song song với nhau thì vectơ pháp tuyến của mặt phẳng này cũng là vectơ pháp tuyến của mặt phẳng kia.
Lời giải chi tiết:
a) Mặt phẳng \(\left( \alpha \right)\) có một vectơ pháp tuyến là: \(\overrightarrow {{n_\alpha }} = \left( {5;2; - 4} \right)\), mặt phẳng \(\left( \beta \right)\) có một vectơ pháp tuyến là: \(\overrightarrow {{n_\beta }} = \left( {10;4; - 2} \right)\).
Vì \(\frac{5}{{10}} = \frac{4}{2} \ne \frac{{ - 4}}{2}\) nên \(\overrightarrow {{n_\alpha }} \) và \(\overrightarrow {{n_\beta }} \) không cùng phương. Do đó, hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) không song song với nhau.
b) Vì \(5.1 - 3.2 - 4.5 + 6 = 5 - 6 - 20 + 6 = - 15 \ne 0\) nên điểm \(M\left( {1; - 3;5} \right)\) không thuộc mặt phẳng \(\left( \alpha \right)\).
Vì \(10.1 + 4.\left( { - 3} \right) - 2.5 + 12 = 0\) nên điểm \(M\left( {1; - 3;5} \right)\) thuộc mặt phẳng \(\left( \beta \right)\).
c) Vì mặt phẳng (P) song song với \(\left( \alpha \right)\) nên mặt phẳng (P) nhận \(\overrightarrow {{n_\alpha }} = \left( {5;2; - 4} \right)\) làm một vectơ pháp tuyến. Mà điểm \(M\left( {1; - 3;5} \right)\) thuộc (P) nên phương trình mặt phẳng (P) là:
\(5\left( {x - 1} \right) + 2\left( {y + 3} \right) - 4\left( {z - 5} \right) = 0 \Leftrightarrow 5x + 2y - 4z + 21 = 0\)
Trả lời câu hỏi Vận dụng 4 trang 37 SGK Toán 12 Kết nối tri thức
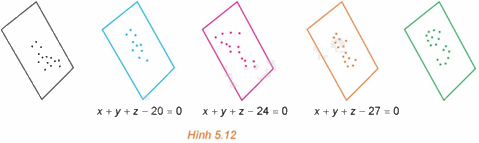
Trong một kì thi tuyển sinh có ba môn thi Toán, Văn, Tiếng Anh. Trong không gian Oxyz, người ta biểu diễn kết quả thi của mỗi thí sinh bởi điểm có hoành độ, tung độ, cao độ tương ứng là điểm Toán, Văn, Tiếng Anh của thí sinh đó.
a) Chứng minh rằng các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 27 (nếu có) cùng thuộc mặt phẳng có phương trình \(x + y + z - 27 = 0\).
b) Chứng minh rằng tồn tại một số mặt phẳng đôi một song song với nhau sao cho hai điểm biểu diễn ứng với hai thí sinh có tổng số điểm thi bằng nhau thì cùng thuộc một mặt phẳng trong số các mặt phẳng đó.
Phương pháp giải:
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để chứng minh: Nếu hai mặt phẳng song song với nhau thì vectơ pháp tuyến của mặt phẳng này cũng là vectơ pháp tuyến của mặt phẳng kia.
Lời giải chi tiết:
a) Gọi điểm Toán, Văn, Tiếng Anh của một thí sinh lần lượt là \({x_0};{y_0};{z_0}\) sao cho tổng điểm của thí sinh đó là 27. Khi đó, \({x_0} + {y_0} + {z_0} = 27\). Suy ra, điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) biểu diễn kết quả thi của thí sinh đó.
Thay \(x = {x_0};y = {y_0},z = {z_0}\) vào phương trình \(x + y + z - 27 = 0\) ta có:
${{x}_{0}}+{{y}_{0}}+{{z}_{0}}-27=0\Leftrightarrow 27-27=0\left( LD \right)$
Do đó, điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) thuộc mặt phẳng có phương trình \(x + y + z - 27 = 0\).
Vậy các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 27 (nếu có) cùng thuộc mặt phẳng có phương trình \(x + y + z - 27 = 0\).
b) Xét phương trình mặt phẳng (M): \(x + y + z - 24 = 0\)
Gọi điểm Toán, Văn, Tiếng Anh của một thí sinh lần lượt là \({x_1};{y_1};{z_1}\) sao cho tổng điểm của thí sinh đó là 24. Khi đó, \({x_1} + {y_1} + {z_1} = 24\). Khi đó, điểm \(A\left( {{x_1};{y_1};{z_1}} \right)\) biểu diễn kết quả thi của thí sinh đó.
Thay \(x = {x_1};y = {y_1},z = {z_1}\) vào phương trình \(x + y + z - 24 = 0\) ta có:
${{x}_{1}}+{{y}_{1}}+{{z}_{1}}-24=0\Leftrightarrow 24-24=0\left( L \right)$
Do đó, điểm \(A\left( {{x_1};{y_1};{z_1}} \right)\) thuộc mặt phẳng có phương trình \(x + y + z - 24 = 0\).
Vậy các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 24 (nếu có) cùng thuộc mặt phẳng (M).
Xét phương trình mặt phẳng (N): \(x + y + z - 20 = 0\)
Gọi điểm Toán, Văn, Tiếng Anh của một thí sinh lần lượt là \({x_2};{y_2};{z_2}\) sao cho tổng điểm của thí sinh đó là 20. Khi đó, \({x_2} + {y_2} + {z_2} = 20\). Khi đó, điểm \(B\left( {{x_2};{y_2};{z_2}} \right)\) biểu diễn kết quả thi của thí sinh đó.
Thay \(x = {x_2};y = {y_2},z = {z_2}\) vào phương trình \(x + y + z - 20 = 0\) ta có:
${{x}_{2}}+{{y}_{2}}+{{z}_{2}}-20=0\Leftrightarrow 20-20=0\left( LD \right)$
Do đó, điểm \(B\left( {{x_2};{y_2};{z_2}} \right)\) thuộc mặt phẳng (N).
Vậy các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 20 cùng thuộc mặt phẳng có phương trình (N).
Theo a, các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 27 cùng thuộc mặt phẳng (P) có phương trình \(x + y + z - 27 = 0\).
Ta thấy ba mặt phẳng (M), (N), (P) có vectơ pháp tuyến \(\overrightarrow n \left( {1;1;1} \right)\) và \( - 24 \ne - 20 \ne - 27\) nên ba mặt phẳng (M), (N), (P) song song với nhau.
Từ đó ta có kết luận: Tồn tại một số mặt phẳng đôi một song song với nhau sao cho hai điểm biểu diễn ứng với hai thí sinh có tổng số điểm thi bằng nhau thì cùng thuộc một mặt phẳng trong số các mặt phẳng đó.
VD4
Trả lời câu hỏi Vận dụng 4 trang 37 SGK Toán 12 Kết nối tri thức
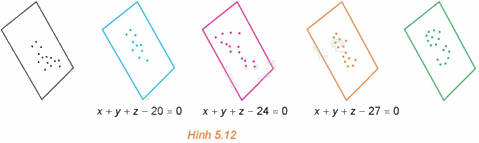
Trong một kì thi tuyển sinh có ba môn thi Toán, Văn, Tiếng Anh. Trong không gian Oxyz, người ta biểu diễn kết quả thi của mỗi thí sinh bởi điểm có hoành độ, tung độ, cao độ tương ứng là điểm Toán, Văn, Tiếng Anh của thí sinh đó.
a) Chứng minh rằng các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 27 (nếu có) cùng thuộc mặt phẳng có phương trình \(x + y + z - 27 = 0\).
b) Chứng minh rằng tồn tại một số mặt phẳng đôi một song song với nhau sao cho hai điểm biểu diễn ứng với hai thí sinh có tổng số điểm thi bằng nhau thì cùng thuộc một mặt phẳng trong số các mặt phẳng đó.
Phương pháp giải:
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để chứng minh: Nếu hai mặt phẳng song song với nhau thì vectơ pháp tuyến của mặt phẳng này cũng là vectơ pháp tuyến của mặt phẳng kia.
Lời giải chi tiết:
a) Gọi điểm Toán, Văn, Tiếng Anh của một thí sinh lần lượt là \({x_0};{y_0};{z_0}\) sao cho tổng điểm của thí sinh đó là 27. Khi đó, \({x_0} + {y_0} + {z_0} = 27\). Suy ra, điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) biểu diễn kết quả thi của thí sinh đó.
Thay \(x = {x_0};y = {y_0},z = {z_0}\) vào phương trình \(x + y + z - 27 = 0\) ta có:
${{x}_{0}}+{{y}_{0}}+{{z}_{0}}-27=0\Leftrightarrow 27-27=0\left( LD \right)$
Do đó, điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) thuộc mặt phẳng có phương trình \(x + y + z - 27 = 0\).
Vậy các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 27 (nếu có) cùng thuộc mặt phẳng có phương trình \(x + y + z - 27 = 0\).
b) Xét phương trình mặt phẳng (M): \(x + y + z - 24 = 0\)
Gọi điểm Toán, Văn, Tiếng Anh của một thí sinh lần lượt là \({x_1};{y_1};{z_1}\) sao cho tổng điểm của thí sinh đó là 24. Khi đó, \({x_1} + {y_1} + {z_1} = 24\). Khi đó, điểm \(A\left( {{x_1};{y_1};{z_1}} \right)\) biểu diễn kết quả thi của thí sinh đó.
Thay \(x = {x_1};y = {y_1},z = {z_1}\) vào phương trình \(x + y + z - 24 = 0\) ta có:
${{x}_{1}}+{{y}_{1}}+{{z}_{1}}-24=0\Leftrightarrow 24-24=0\left( L \right)$
Do đó, điểm \(A\left( {{x_1};{y_1};{z_1}} \right)\) thuộc mặt phẳng có phương trình \(x + y + z - 24 = 0\).
Vậy các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 24 (nếu có) cùng thuộc mặt phẳng (M).
Xét phương trình mặt phẳng (N): \(x + y + z - 20 = 0\)
Gọi điểm Toán, Văn, Tiếng Anh của một thí sinh lần lượt là \({x_2};{y_2};{z_2}\) sao cho tổng điểm của thí sinh đó là 20. Khi đó, \({x_2} + {y_2} + {z_2} = 20\). Khi đó, điểm \(B\left( {{x_2};{y_2};{z_2}} \right)\) biểu diễn kết quả thi của thí sinh đó.
Thay \(x = {x_2};y = {y_2},z = {z_2}\) vào phương trình \(x + y + z - 20 = 0\) ta có:
${{x}_{2}}+{{y}_{2}}+{{z}_{2}}-20=0\Leftrightarrow 20-20=0\left( LD \right)$
Do đó, điểm \(B\left( {{x_2};{y_2};{z_2}} \right)\) thuộc mặt phẳng (N).
Vậy các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 20 cùng thuộc mặt phẳng có phương trình (N).
Theo a, các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 27 cùng thuộc mặt phẳng (P) có phương trình \(x + y + z - 27 = 0\).
Ta thấy ba mặt phẳng (M), (N), (P) có vectơ pháp tuyến \(\overrightarrow n \left( {1;1;1} \right)\) và \( - 24 \ne - 20 \ne - 27\) nên ba mặt phẳng (M), (N), (P) song song với nhau.
Từ đó ta có kết luận: Tồn tại một số mặt phẳng đôi một song song với nhau sao cho hai điểm biểu diễn ứng với hai thí sinh có tổng số điểm thi bằng nhau thì cùng thuộc một mặt phẳng trong số các mặt phẳng đó.
Giải mục 5 trang 37,38 SGK Toán 12 tập 2 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 5 trang 37,38 SGK Toán 12 tập 2 - Kết nối tri thức tập trung vào việc ôn tập chương 3: Đạo hàm. Đây là một phần quan trọng trong chương trình Toán 12, đòi hỏi học sinh phải nắm vững các khái niệm, định lý và kỹ năng liên quan đến đạo hàm. Bài tập trong mục này thường bao gồm các dạng bài tập về tính đạo hàm, ứng dụng đạo hàm để khảo sát hàm số, và giải các bài toán thực tế liên quan đến đạo hàm.
Nội dung chi tiết các bài tập trong mục 5
Mục 5 bao gồm các bài tập từ 3.1 đến 3.6, mỗi bài tập tập trung vào một khía cạnh khác nhau của đạo hàm. Dưới đây là nội dung chi tiết của từng bài tập:
- Bài 3.1: Tính đạo hàm của các hàm số đơn giản. Bài tập này giúp học sinh ôn lại các quy tắc tính đạo hàm cơ bản, như quy tắc đạo hàm của tổng, hiệu, tích, thương, và quy tắc đạo hàm của hàm hợp.
- Bài 3.2: Tính đạo hàm của các hàm số lượng giác. Bài tập này yêu cầu học sinh phải nhớ và áp dụng các công thức đạo hàm của các hàm số lượng giác, như sinx, cosx, tanx, cotx.
- Bài 3.3: Tính đạo hàm của các hàm số mũ và logarit. Bài tập này giúp học sinh ôn lại các công thức đạo hàm của các hàm số mũ và logarit, và cách áp dụng chúng để tính đạo hàm của các hàm số phức tạp hơn.
- Bài 3.4: Ứng dụng đạo hàm để khảo sát hàm số. Bài tập này yêu cầu học sinh phải sử dụng đạo hàm để tìm các điểm cực trị, khoảng đồng biến, khoảng nghịch biến, và điểm uốn của hàm số.
- Bài 3.5: Giải các bài toán thực tế liên quan đến đạo hàm. Bài tập này giúp học sinh hiểu được ứng dụng của đạo hàm trong thực tế, như tính vận tốc, gia tốc, và tối ưu hóa các bài toán kinh tế.
- Bài 3.6: Ôn tập tổng hợp về đạo hàm. Bài tập này bao gồm các bài tập tổng hợp về đạo hàm, giúp học sinh củng cố kiến thức và kỹ năng đã học.
Phương pháp giải các bài tập trong mục 5
Để giải các bài tập trong mục 5 một cách hiệu quả, học sinh cần nắm vững các phương pháp sau:
- Nắm vững các quy tắc tính đạo hàm cơ bản: Quy tắc đạo hàm của tổng, hiệu, tích, thương, hàm hợp, hàm lượng giác, hàm mũ, hàm logarit.
- Sử dụng đạo hàm để khảo sát hàm số: Tìm các điểm cực trị, khoảng đồng biến, khoảng nghịch biến, điểm uốn.
- Áp dụng đạo hàm để giải các bài toán thực tế: Tính vận tốc, gia tốc, tối ưu hóa.
- Luyện tập thường xuyên: Làm nhiều bài tập khác nhau để rèn luyện kỹ năng và củng cố kiến thức.
Lời giải chi tiết bài tập mục 5 trang 37,38
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 5 trang 37,38 SGK Toán 12 tập 2 - Kết nối tri thức:
| Bài tập | Lời giải |
|---|---|
| 3.1a | f'(x) = 2x + 3 |
| 3.1b | f'(x) = -5x2 + 4x |
| 3.2a | f'(x) = cosx |
| ... | ... |
Lưu ý: Đây chỉ là một phần nhỏ của lời giải chi tiết. Để xem đầy đủ lời giải cho tất cả các bài tập, vui lòng truy cập tusach.vn.
Kết luận
Hy vọng rằng lời giải chi tiết mục 5 trang 37,38 SGK Toán 12 tập 2 - Kết nối tri thức trên tusach.vn sẽ giúp bạn hiểu rõ hơn về đạo hàm và tự tin hơn trong quá trình học tập. Chúc bạn học tốt!