Giải mục 2 trang 22,23,24 SGK Toán 12 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải mục 2 trang 22,23,24 SGK Toán 12 tập 2 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 22, 23, 24 sách giáo khoa Toán 12 tập 2 chương trình Kết nối tri thức. Bài giải này được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm, đảm bảo tính chính xác và giúp học sinh nắm vững kiến thức.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, Tusach.vn luôn cố gắng cung cấp những tài liệu học tập chất lượng nhất, hỗ trợ học sinh học tập hiệu quả.
Ứng dụng tích phân để tính thể tích vật thể
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 22 SGK Toán 12 Kết nối tri thức
Xét hình trụ có bán kính đáy R, có trục là trục hoành Ox, nằm giữa hai mặt phẳng \(x = a\) và \(x = b\left( {a < b} \right)\) (H.4.20).
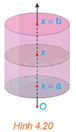
a) Tính thể tích V của hình trụ.
b) Tính diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x \(\left( {a \le x \le b} \right)\). Từ đó tính \(\int\limits_a^b {S\left( x \right)dx} \) và so sánh với V.
Phương pháp giải:
Sử dụng kiến thức về thể tích hình trụ để tính: Hình trụ có bán kính đáy R và chiều cao h thì có thể tích là: \(V = \pi {R^2}h\)
Lời giải chi tiết:
a) Thể tích V của hình trụ là: \(V = \pi {R^2}h = \pi {R^2}\left( {b - a} \right)\) (h là chiều cao của hình trụ)
b) Diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x là: \(S\left( x \right) = \pi {R^2}\).
Ta có: \(\int\limits_a^b {S\left( x \right)dx} = \int\limits_a^b {\pi {R^2}dx} = \pi {R^2}x\left| \begin{array}{l}b\\a\end{array} \right. = \pi {R^2}\left( {b - a} \right)\). Do đó, \(V = \int\limits_a^b {S\left( x \right)dx} \).
VD2
Trả lời câu hỏi Vận dụng 2 trang 23 SGK Toán 12 Kết nối tri thức
Tính thể tích của khối chóp cụt đều có diện tích hai đáy là \({S_o},{S_1}\) và chiều cao bằng h (H.4.24). Từ đó suy ra công thức tính thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h.
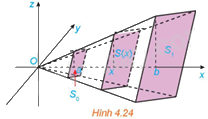
Phương pháp giải:
Sử dụng kiến thức về công thức tính thể tích vật để để tính: Cho một vật thể trong không gian Oxyz. Gọi \(\beta \) là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm có hoành độ \(x = a,x = b\). Một mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x cắt vật thể theo mặt cắt có diện tích là S(x). Giả sử S(x) là hàm số liên tục trên đoạn [a; b]. Khi đó thể tích V của phần vật thể \(\beta \) được tính bởi công thức \(V = \int\limits_a^b {S\left( x \right)dx} \).
Lời giải chi tiết:
Trong hệ trục tọa độ Oxyz, ta đặt khối chóp (tạo ra khối chóp cụt) sao cho đường cao nằm trên trục Ox và đỉnh trùng với gốc tọa độ.
Gọi a và b lần lượt là khoảng cách từ O đến đáy nhỏ và đáy lớn. Khi đó, chiều cao của khối chóp cụt là: \(h = b - a\).
Thiết diện của khối chóp cụt đều cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x \(\left( {a \le x \le b} \right)\) là một đa giác đều đồng dạng với đáy lớn với tỉ số đồng dạng là \(\frac{x}{b}\).
Ta có: \(\frac{{S\left( x \right)}}{{{S_1}}} = \frac{{{x^2}}}{{{b^2}}}\) nên \(S\left( x \right) = {S_1}.\frac{{{x^2}}}{{{b^2}}}\).
Thể tích của khối chóp cụt đều là:
\(V = \int\limits_a^b {{S_1}\frac{{{x^2}}}{{{b^2}}}dx} = \frac{{{S_1}\left( {{b^3} - {a^3}} \right)}}{{3{b^2}}} = \frac{{b - a}}{3}.\frac{{{S_1}{a^2} + {S_1}ab + {S_1}{b^2}}}{{{b^2}}} = \frac{h}{3}\left( {\frac{{{S_1}{a^2}}}{{{b^2}}} + \frac{{{S_1}a}}{b} + {S_1}} \right)\)
Lại có: \({S_0} = S\left( a \right) = \frac{{{S_1}{a^2}}}{{{b^2}}},\frac{{{S_1}a}}{b} = \sqrt {{S_1}.\frac{{{S_1}{a^2}}}{{{b^2}}}} = \sqrt {{S_1}{S_0}} \). Do đó, \(V = \frac{h}{3}\left( {{S_0} + \sqrt {{S_0}{S_1}} + {S_1}} \right)\)
Khối chóp đều được coi là khối chóp cụt đều có \({S_0} = 0\). Do đó, thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h là: \(V = \frac{1}{3}S.h\).
VD3
Trả lời câu hỏi Vận dụng 3 trang 25 SGK Toán 12 Kết nối tri thức
a) Tính thể tích của khối tròn xoay sinh ra khi quay hình thang vuông OABC trong mặt phẳng Oxy với \(OA = h,AB = R\) và \(OC = r\), quanh trục Ox (H.4.28).
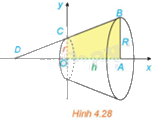
b) Từ công thức thu được ở phần a, hãy rút ra công thức tính thể tích của khối nón có bán kính đáy bằng R và chiều cao h.
Phương pháp giải:
Sử dụng kiến thức về công thức tính thể tích của khối tròn xoay để tính: Cho hàm số f(x) liên tục, không âm trên đoạn [a; b]. Khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\) xung quanh trục hoành, ta được hình khối gọi là một khối tròn xoay. Khi cắt khối tròn xoay đó bởi một mặt phẳng vuông góc với trục Ox tại điểm \(x \in \left[ {a;b} \right]\) được một hình tròn có bán kính f(x). Thể tích của khối tròn xoay này là: \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \).
Lời giải chi tiết:
a)
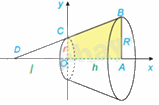
Ta có: \(C\left( {0;r} \right),B\left( {h,R} \right) \Rightarrow \overrightarrow {BC} \left( { - h,r - R} \right) \Rightarrow \overrightarrow n \left( {r - R,h} \right)\)
Phương trình đường thẳng BC là: \(\left( {r - R} \right)x + h\left( {y - r} \right) = 0 \Leftrightarrow y = \frac{{hr + \left( {R - r} \right)x}}{h}\)
Thể tích hình cần tính là:
\(V = \pi \int\limits_0^h {{{\left[ {\frac{{hr + \left( {R - r} \right)x}}{h}} \right]}^2}dx} = \pi \int\limits_0^h {{{\left[ {r + \frac{{\left( {R - r} \right)x}}{h}} \right]}^2}dx} = \pi \int\limits_0^h {\left[ {{r^2} + \frac{{2r\left( {R - r} \right)x}}{h} + \frac{{{{\left( {R - r} \right)}^2}{x^2}}}{{{h^2}}}} \right]dx} \)
\( = \pi \left( {{r^2}x + \frac{{r\left( {R - r} \right){x^2}}}{h} + \frac{{{{\left( {R - r} \right)}^2}{x^3}}}{{3{h^2}}}} \right)\left| \begin{array}{l}h\\0\end{array} \right. = \pi \left( {{r^2}h + \frac{{r\left( {R - r} \right){h^2}}}{h} + \frac{{{{\left( {R - r} \right)}^2}{h^3}}}{{3{h^2}}}} \right)\)
\( = \pi \left( {{r^2}h + r\left( {R - r} \right)h + \frac{{{{\left( {R - r} \right)}^2}h}}{3}} \right) = \pi \left( {{r^2}h + rRh - {r^2}h + \frac{{{R^2}h}}{3} - \frac{{2rRh}}{3} + \frac{{{r^2}h}}{3}} \right)\)
\( = \pi \left( {\frac{{rRh}}{3} + \frac{{{R^2}h}}{3} + \frac{{{r^2}h}}{3}} \right) = \frac{1}{3}\pi h\left( {{R^2} + rR + {r^2}} \right)\)
b) Khi \(r = 0\) thì khối nón cụt trở thành khối nón có chiều cao h và bán kính đáy R. Do đó, thể tích khối nón là: \(V = \frac{1}{3}\pi {R^2}h\).
HĐ4
Trả lời câu hỏi Hoạt động 4 trang 24 SGK Toán 12 Kết nối tri thức
Xét hình phẳng giới hạn bởi đồ thị hàm số \(f\left( x \right) = \frac{1}{2}x\), trục hoành và hai đường thẳng \(x = 0,x = 4\). Khi quay hình phẳng này xung quanh trục hoành Ox ta được khối nón có đỉnh là gốc O, trục là Ox và đáy là hình tròn bán kính bằng 2 (H.4.25).
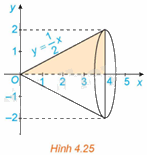
a) Tính thể tích V của khối nón.
b) Chứng minh rằng khi cắt khối nón bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x \(\left( {0 \le x \le 4} \right)\) thì mặt cắt thu được là một hình tròn có bán kính là f(x), do đó diện tích mặt cắt là \(S\left( x \right) = \pi {f^2}\left( x \right)\). Tính \(\pi \int\limits_0^4 {{f^2}\left( x \right)dx} \) và so sánh với V.
Phương pháp giải:
Sử dụng kiến thức về thể tích khối nón để tính: Thể tích của khối nón có bán kính R, chiều cao h là: \(V = \frac{1}{3}\pi {R^2}h\).
Lời giải chi tiết:
a) Thể tích của khối nón là: \(V = \frac{1}{3}.\pi {.2^2}.4 = \frac{{16\pi }}{3}\)
b)
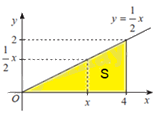
Khi cắt khối nón bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x \(\left( {0 \le x \le 4} \right)\) thì mặt cắt thu được là một hình tròn có bán kính là \(f\left( x \right) = \frac{1}{2}x\).
Diện tích mặt cắt là: \(S\left( x \right) = \pi {f^2}\left( x \right) = \frac{1}{4}\pi {x^2}\).
Ta có: \(\pi \int\limits_0^4 {{f^2}\left( x \right)dx} = \pi \int\limits_0^4 {\frac{1}{4}{x^2}dx = \frac{{\pi {x^3}}}{{12}}\left| \begin{array}{l}4\\0\end{array} \right. = } \frac{{16\pi }}{3}\). Do đó, \(V = \pi \int\limits_0^4 {{f^2}\left( x \right)dx} \).
- HĐ3
- VD2
- HĐ4
- VD3
Trả lời câu hỏi Hoạt động 3 trang 22 SGK Toán 12 Kết nối tri thức
Xét hình trụ có bán kính đáy R, có trục là trục hoành Ox, nằm giữa hai mặt phẳng \(x = a\) và \(x = b\left( {a < b} \right)\) (H.4.20).
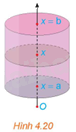
a) Tính thể tích V của hình trụ.
b) Tính diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x \(\left( {a \le x \le b} \right)\). Từ đó tính \(\int\limits_a^b {S\left( x \right)dx} \) và so sánh với V.
Phương pháp giải:
Sử dụng kiến thức về thể tích hình trụ để tính: Hình trụ có bán kính đáy R và chiều cao h thì có thể tích là: \(V = \pi {R^2}h\)
Lời giải chi tiết:
a) Thể tích V của hình trụ là: \(V = \pi {R^2}h = \pi {R^2}\left( {b - a} \right)\) (h là chiều cao của hình trụ)
b) Diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x là: \(S\left( x \right) = \pi {R^2}\).
Ta có: \(\int\limits_a^b {S\left( x \right)dx} = \int\limits_a^b {\pi {R^2}dx} = \pi {R^2}x\left| \begin{array}{l}b\\a\end{array} \right. = \pi {R^2}\left( {b - a} \right)\). Do đó, \(V = \int\limits_a^b {S\left( x \right)dx} \).
Trả lời câu hỏi Vận dụng 2 trang 23 SGK Toán 12 Kết nối tri thức
Tính thể tích của khối chóp cụt đều có diện tích hai đáy là \({S_o},{S_1}\) và chiều cao bằng h (H.4.24). Từ đó suy ra công thức tính thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h.

Phương pháp giải:
Sử dụng kiến thức về công thức tính thể tích vật để để tính: Cho một vật thể trong không gian Oxyz. Gọi \(\beta \) là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm có hoành độ \(x = a,x = b\). Một mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x cắt vật thể theo mặt cắt có diện tích là S(x). Giả sử S(x) là hàm số liên tục trên đoạn [a; b]. Khi đó thể tích V của phần vật thể \(\beta \) được tính bởi công thức \(V = \int\limits_a^b {S\left( x \right)dx} \).
Lời giải chi tiết:
Trong hệ trục tọa độ Oxyz, ta đặt khối chóp (tạo ra khối chóp cụt) sao cho đường cao nằm trên trục Ox và đỉnh trùng với gốc tọa độ.
Gọi a và b lần lượt là khoảng cách từ O đến đáy nhỏ và đáy lớn. Khi đó, chiều cao của khối chóp cụt là: \(h = b - a\).
Thiết diện của khối chóp cụt đều cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x \(\left( {a \le x \le b} \right)\) là một đa giác đều đồng dạng với đáy lớn với tỉ số đồng dạng là \(\frac{x}{b}\).
Ta có: \(\frac{{S\left( x \right)}}{{{S_1}}} = \frac{{{x^2}}}{{{b^2}}}\) nên \(S\left( x \right) = {S_1}.\frac{{{x^2}}}{{{b^2}}}\).
Thể tích của khối chóp cụt đều là:
\(V = \int\limits_a^b {{S_1}\frac{{{x^2}}}{{{b^2}}}dx} = \frac{{{S_1}\left( {{b^3} - {a^3}} \right)}}{{3{b^2}}} = \frac{{b - a}}{3}.\frac{{{S_1}{a^2} + {S_1}ab + {S_1}{b^2}}}{{{b^2}}} = \frac{h}{3}\left( {\frac{{{S_1}{a^2}}}{{{b^2}}} + \frac{{{S_1}a}}{b} + {S_1}} \right)\)
Lại có: \({S_0} = S\left( a \right) = \frac{{{S_1}{a^2}}}{{{b^2}}},\frac{{{S_1}a}}{b} = \sqrt {{S_1}.\frac{{{S_1}{a^2}}}{{{b^2}}}} = \sqrt {{S_1}{S_0}} \). Do đó, \(V = \frac{h}{3}\left( {{S_0} + \sqrt {{S_0}{S_1}} + {S_1}} \right)\)
Khối chóp đều được coi là khối chóp cụt đều có \({S_0} = 0\). Do đó, thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h là: \(V = \frac{1}{3}S.h\).
Trả lời câu hỏi Hoạt động 4 trang 24 SGK Toán 12 Kết nối tri thức
Xét hình phẳng giới hạn bởi đồ thị hàm số \(f\left( x \right) = \frac{1}{2}x\), trục hoành và hai đường thẳng \(x = 0,x = 4\). Khi quay hình phẳng này xung quanh trục hoành Ox ta được khối nón có đỉnh là gốc O, trục là Ox và đáy là hình tròn bán kính bằng 2 (H.4.25).

a) Tính thể tích V của khối nón.
b) Chứng minh rằng khi cắt khối nón bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x \(\left( {0 \le x \le 4} \right)\) thì mặt cắt thu được là một hình tròn có bán kính là f(x), do đó diện tích mặt cắt là \(S\left( x \right) = \pi {f^2}\left( x \right)\). Tính \(\pi \int\limits_0^4 {{f^2}\left( x \right)dx} \) và so sánh với V.
Phương pháp giải:
Sử dụng kiến thức về thể tích khối nón để tính: Thể tích của khối nón có bán kính R, chiều cao h là: \(V = \frac{1}{3}\pi {R^2}h\).
Lời giải chi tiết:
a) Thể tích của khối nón là: \(V = \frac{1}{3}.\pi {.2^2}.4 = \frac{{16\pi }}{3}\)
b)

Khi cắt khối nón bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x \(\left( {0 \le x \le 4} \right)\) thì mặt cắt thu được là một hình tròn có bán kính là \(f\left( x \right) = \frac{1}{2}x\).
Diện tích mặt cắt là: \(S\left( x \right) = \pi {f^2}\left( x \right) = \frac{1}{4}\pi {x^2}\).
Ta có: \(\pi \int\limits_0^4 {{f^2}\left( x \right)dx} = \pi \int\limits_0^4 {\frac{1}{4}{x^2}dx = \frac{{\pi {x^3}}}{{12}}\left| \begin{array}{l}4\\0\end{array} \right. = } \frac{{16\pi }}{3}\). Do đó, \(V = \pi \int\limits_0^4 {{f^2}\left( x \right)dx} \).
Trả lời câu hỏi Vận dụng 3 trang 25 SGK Toán 12 Kết nối tri thức
a) Tính thể tích của khối tròn xoay sinh ra khi quay hình thang vuông OABC trong mặt phẳng Oxy với \(OA = h,AB = R\) và \(OC = r\), quanh trục Ox (H.4.28).

b) Từ công thức thu được ở phần a, hãy rút ra công thức tính thể tích của khối nón có bán kính đáy bằng R và chiều cao h.
Phương pháp giải:
Sử dụng kiến thức về công thức tính thể tích của khối tròn xoay để tính: Cho hàm số f(x) liên tục, không âm trên đoạn [a; b]. Khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\) xung quanh trục hoành, ta được hình khối gọi là một khối tròn xoay. Khi cắt khối tròn xoay đó bởi một mặt phẳng vuông góc với trục Ox tại điểm \(x \in \left[ {a;b} \right]\) được một hình tròn có bán kính f(x). Thể tích của khối tròn xoay này là: \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \).
Lời giải chi tiết:
a)
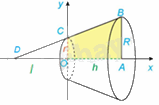
Ta có: \(C\left( {0;r} \right),B\left( {h,R} \right) \Rightarrow \overrightarrow {BC} \left( { - h,r - R} \right) \Rightarrow \overrightarrow n \left( {r - R,h} \right)\)
Phương trình đường thẳng BC là: \(\left( {r - R} \right)x + h\left( {y - r} \right) = 0 \Leftrightarrow y = \frac{{hr + \left( {R - r} \right)x}}{h}\)
Thể tích hình cần tính là:
\(V = \pi \int\limits_0^h {{{\left[ {\frac{{hr + \left( {R - r} \right)x}}{h}} \right]}^2}dx} = \pi \int\limits_0^h {{{\left[ {r + \frac{{\left( {R - r} \right)x}}{h}} \right]}^2}dx} = \pi \int\limits_0^h {\left[ {{r^2} + \frac{{2r\left( {R - r} \right)x}}{h} + \frac{{{{\left( {R - r} \right)}^2}{x^2}}}{{{h^2}}}} \right]dx} \)
\( = \pi \left( {{r^2}x + \frac{{r\left( {R - r} \right){x^2}}}{h} + \frac{{{{\left( {R - r} \right)}^2}{x^3}}}{{3{h^2}}}} \right)\left| \begin{array}{l}h\\0\end{array} \right. = \pi \left( {{r^2}h + \frac{{r\left( {R - r} \right){h^2}}}{h} + \frac{{{{\left( {R - r} \right)}^2}{h^3}}}{{3{h^2}}}} \right)\)
\( = \pi \left( {{r^2}h + r\left( {R - r} \right)h + \frac{{{{\left( {R - r} \right)}^2}h}}{3}} \right) = \pi \left( {{r^2}h + rRh - {r^2}h + \frac{{{R^2}h}}{3} - \frac{{2rRh}}{3} + \frac{{{r^2}h}}{3}} \right)\)
\( = \pi \left( {\frac{{rRh}}{3} + \frac{{{R^2}h}}{3} + \frac{{{r^2}h}}{3}} \right) = \frac{1}{3}\pi h\left( {{R^2} + rR + {r^2}} \right)\)
b) Khi \(r = 0\) thì khối nón cụt trở thành khối nón có chiều cao h và bán kính đáy R. Do đó, thể tích khối nón là: \(V = \frac{1}{3}\pi {R^2}h\).
Giải mục 2 trang 22,23,24 SGK Toán 12 tập 2 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 2 trang 22, 23, 24 SGK Toán 12 tập 2 - Kết nối tri thức tập trung vào việc ôn tập chương 3: Đạo hàm. Đây là một phần quan trọng trong chương trình Toán 12, đòi hỏi học sinh phải nắm vững các khái niệm, định lý và kỹ năng liên quan đến đạo hàm. Việc giải các bài tập trong mục này sẽ giúp học sinh củng cố kiến thức và chuẩn bị tốt cho các kỳ thi sắp tới.
Nội dung chính của Mục 2
- Ôn tập lý thuyết: Mục này nhắc lại các khái niệm cơ bản về đạo hàm, bao gồm định nghĩa, ý nghĩa hình học và vật lý của đạo hàm, các quy tắc tính đạo hàm, đạo hàm của các hàm số thường gặp (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit).
- Bài tập vận dụng: Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, bao gồm tính đạo hàm, tìm cực trị, khảo sát hàm số, giải phương trình và bất phương trình.
Phương pháp giải các bài tập trong Mục 2
- Nắm vững lý thuyết: Đây là bước quan trọng nhất để giải quyết các bài tập về đạo hàm. Học sinh cần hiểu rõ định nghĩa, ý nghĩa và các quy tắc tính đạo hàm.
- Xác định đúng dạng bài: Mỗi bài tập về đạo hàm thường thuộc một dạng nhất định. Việc xác định đúng dạng bài sẽ giúp học sinh lựa chọn phương pháp giải phù hợp.
- Sử dụng các công thức và quy tắc: Khi giải bài tập, học sinh cần sử dụng các công thức và quy tắc tính đạo hàm một cách chính xác.
- Kiểm tra lại kết quả: Sau khi giải xong bài tập, học sinh nên kiểm tra lại kết quả để đảm bảo tính chính xác.
Giải chi tiết các bài tập trong Mục 2
Dưới đây là lời giải chi tiết cho các bài tập trong Mục 2 trang 22, 23, 24 SGK Toán 12 tập 2 - Kết nối tri thức:
Bài 1: Tính đạo hàm của các hàm số sau:
a) y = x3 - 2x2 + 5x - 1
b) y = sin(2x) + cos(x)
c) y = ex + ln(x)
Giải:
- a) y' = 3x2 - 4x + 5
- b) y' = 2cos(2x) - sin(x)
- c) y' = ex + 1/x
Bài 2: Tìm cực trị của hàm số y = x3 - 3x2 + 2
Giải:
y' = 3x2 - 6x
Giải phương trình y' = 0, ta được x = 0 hoặc x = 2
Lập bảng biến thiên, ta thấy hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2
Lời khuyên khi học tập
Để học tốt môn Toán 12, đặc biệt là phần đạo hàm, học sinh cần:
- Học thuộc các công thức và quy tắc tính đạo hàm.
- Luyện tập thường xuyên các bài tập về đạo hàm.
- Tìm hiểu các ứng dụng của đạo hàm trong thực tế.
- Tham khảo các tài liệu học tập khác, chẳng hạn như sách bài tập, đề thi thử.
Tusach.vn hy vọng rằng lời giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về Mục 2 trang 22, 23, 24 SGK Toán 12 tập 2 - Kết nối tri thức và đạt kết quả tốt trong học tập.