Giải mục 2 trang 36, 37, 38 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 2 trang 36, 37, 38 SGK Toán 12 tập 1 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 36, 37, 38 SGK Toán 12 tập 1 chương trình Kết nối tri thức. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, từ đó áp dụng kiến thức vào các bài tập khác một cách hiệu quả.
Tốc độ thay đổi của một đại lượng
LT2
Trả lời câu hỏi Luyện tập 2 trang 38 SGK Toán 12 Kết nối tri thức
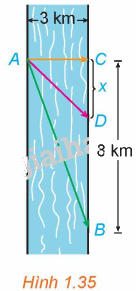
Anh An chèo thuyền từ điểm A trên bờ một con sông thẳng rộng 3km và muốn đến điểm B ở bờ đối diện cách 8km về phía hạ lưu càng nhanh càng tốt (H.1.35). Anh An có thể chèo thuyền trực tiếp qua sông đến điểm C rồi chạy bộ đến B, hoặc anh có thể chèo thuyển thẳng đến B, hoặc anh cũng có thể chèo thuyền đến một điểm D nào đó giữa C và B rồi chạy bộ đến B. Nếu vận tốc chèo thuyền là 6km/h và vận tốc chạy bộ là 8km/h thì anh An phải chèo thuyền sang bờ ở điểm nào để đến B càng sớm càng tốt? (Giả sử rằng vận tốc của nước là không đáng kể so với vận tốc chèo thuyền của anh An).
Phương pháp giải:
Sử dụng kiến thức về cách giải bài toán tối ưu hóa đơn giản để tính:
Bước 1: Xác định đại lượng Q mà ta cần làm cho giá trị của đại lượng ấy lớn nhất hoặc nhỏ nhất và biểu diễn nó qua các đại lượng khác trong bài toán.
Bước 2: Chọn một đại lượng thích hợp nào đó, kí hiệu là x, và biểu diễn các đại lượng khác ở Bước 1 theo x. Khi đó, đại lượng Q sẽ là hàm số của một biến x. Tìm tập xác định của hàm số \(Q = Q\left( x \right)\).
Bước 3: Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số \(Q = Q\left( x \right)\) bằng các phương pháp đã biết và kết luận.
Lời giải chi tiết:
Gọi độ dài đoạn CD là x (km \(0 < x < 8\))
Quãng đường AD dài: \(\sqrt {A{C^2} + D{C^2}} = \sqrt {9 + {x^2}} \left( {km} \right)\)
Quãng đường BD dài \(8 - x\left( {km} \right)\)
Thời gian người đó đi đến B bằng cách chèo thuyền đến một điểm D nào đó giữa C và B rồi chạy bộ đến B là: \(\frac{{\sqrt {9 + {x^2}} }}{6} + \frac{{8 - x}}{8}\) (giờ)
Xét hàm số \(y = \frac{{\sqrt {9 + {x^2}} }}{6} + \frac{{8 - x}}{8}\) với \(0 < x < 8\)
Ta có: \(y' = \frac{x}{{6\sqrt {9 + {x^2}} }} - \frac{1}{8}\)
\(y' = 0 \Leftrightarrow \frac{x}{{6\sqrt {9 + {x^2}} }} - \frac{1}{8} = 0 \Leftrightarrow 4x = 3\sqrt {9 + {x^2}} \Leftrightarrow \left\{ \begin{array}{l}16{x^2} = 9\left( {9 + {x^2}} \right)\\x > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} = \frac{{81}}{7}\\x > 0\end{array} \right. \Leftrightarrow x = \frac{9}{{\sqrt 7 }}\)
Bảng biến thiên:
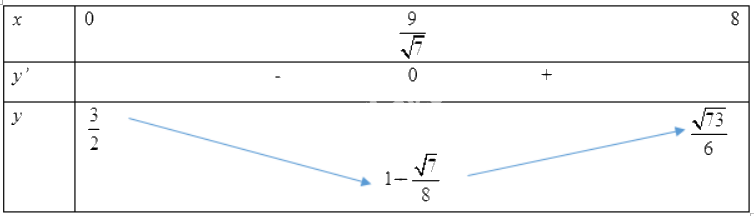
Vậy anh An phải chèo thuyền sang bờ ở điểm D cách C một khoảng bằng \(\frac{9}{{\sqrt 7 }}km\) thì đến B sớm nhất.
VD
Trả lời câu hỏi Vận dụng trang 40 SGK Toán 12 Kết nối tri thức
Một nhà sản xuất trung bình bán được 1 000 ti vi màn hình phẳng mỗi tuần với giá 14 triệu đồng một chiếc. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 500 nghìn đồng, số lượng ti vi bán ra sẽ tăng thêm khoảng 100 ti vi mỗi tuần.
a) Tìm hàm cầu.
b) Công ty nên giảm giá bao nhiêu cho người mua để doanh thu là lớn nhất?
c) Nếu hàm chi phí hằng tuần là \(C\left( x \right) = 12\;000 - 3x\) (triệu đồng), trong đó x là số ti vi bán ra trong tuần, nhà sản xuất nên đặt giá bán như thế nào để lợi nhuận là lớn nhất?
Phương pháp giải:
a) Sử dụng kiến thức về hàm cầu để tìm hàm cầu: Gọi p(x) là giá bán mỗi đơn vị mà công ty có thể tính nếu bán x đơn vị. Khi đó, p được gọi là hàm cầu (hay hàm giá).
b) Sử dụng kiến thức về hàm doanh thu để tính: Nếu x đơn vị được bán và giá mỗi đơn vị là p(x) thì tổng doanh thu là: R(x)=x.p(x), khi đó R(x) được gọi là hàm doanh thu.
c) Nếu x đơn vị được bán thì tổng lợi nhuận là \(P\left( x \right) = R\left( x \right) - C\left( x \right)\) thì P(x) là hàm lợi nhuận và C(x) là hàm chi phí.
Sử dụng kiến thức về cách giải bài toán tối ưu hóa đơn giản để tính:
Bước 1: Xác định đại lượng Q mà ta cần làm cho giá trị của đại lượng ấy lớn nhất hoặc nhỏ nhất và biểu diễn nó qua các đại lượng khác trong bài toán.
Bước 2: Chọn một đại lượng thích hợp nào đó, kí hiệu là x, và biểu diễn các đại lượng khác ở Bước 1 theo x. Khi đó, đại lượng Q sẽ là hàm số của một biến x. Tìm tập xác định của hàm số \(Q = Q\left( x \right)\).
Bước 3: Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số \(Q = Q\left( x \right)\) bằng các phương pháp đã biết và kết luận.
Lời giải chi tiết:
a) Gọi p (triệu đồng) là giá của mỗi ti vi, x là số ti vi. Khi đó, hàm cầu là \(p = p\left( x \right)\).
Theo giả thiết, tốc độ thay đổi của x tỉ lệ với tốc độ thay đổi của p nên hàm số \(p = p\left( x \right)\) là hàm số bậc nhất nên. Do đó, \(p\left( x \right) = ax + b\) (a khác 0).
Giá tiền \({p _1} = 14\) ứng với \({x_1} = 1\;000\), giá tiền \({p_2} = 13,5\) ứng với \({x_2} = 1\;000 + 100 = 1\;100\)
Do đó, phương trình đường thẳng \(p\left( x \right) = ax + b\) đi qua hai điểm (1000; 14) và (1 100; 13,5). Ta có hệ phương trình: \(\left\{ \begin{array}{l}14 = 1\;000a + b\\13,5 = 1\;100a + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{ - 1}}{{200}}\\b = 19\end{array} \right.\) (thỏa mãn)
Vậy hàm cầu là: \(p\left( x \right) = - \frac{1}{{200}}x + 19\)
b) Vì \(p = \frac{{ - 1}}{{200}}x + 19 \Rightarrow x = - 200p + 3\;800\)
Hàm doanh thu từ tiền bán ti vi là: \(R\left( p \right) = px = p\left( { - 200p + 3\;800} \right) = - 200{p^2} + 3\;800p\)
Để doanh thu là lớn nhất thì ta cần tìm p sao cho R đạt giá trị lớn nhất.
Ta có: \(R'\left( p \right) = - 400p + 3\;800,R'\left( p \right) = 0 \Leftrightarrow p = \frac{{19}}{2}\)
Bảng biến thiên:
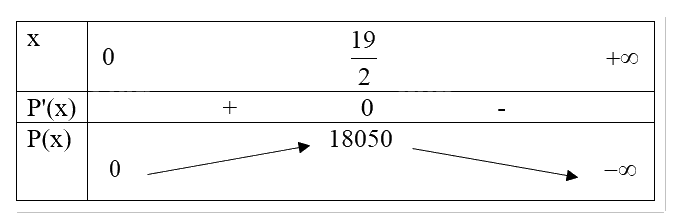
Vậy công ty nên giảm giá số tiền một chiếc ti vi là: \(14 - \frac{{19}}{2} = 4,5\) (triệu đồng) thì doanh thu là lớn nhất.
c) Doanh thu bán hàng của x sản phẩm là: \(R\left( x \right) = x.p\left( x \right) = x.\left( {\frac{{ - 1}}{{200}}x + 19} \right) = \frac{{ - {x^2}}}{{200}} + 19x\) (triệu đồng)
Do đó, hàm số thể hiện lợi nhuận thu được khi bán x sản phẩm là:
\(P\left( x \right) = R\left( x \right) - C\left( x \right) = \frac{{ - {x^2}}}{{200}} + 19x - 12\;000 + 3x = \frac{{ - {x^2}}}{{200}} + 22x - 12\;000\) (triệu đồng).
Để lợi nhuận là lớn nhất thì P(x) là lớn nhất.
Ta có: \(P'\left( x \right) = \frac{{ - x}}{{100}} + 22,P'\left( x \right) = 0 \Leftrightarrow x = 2\;200\)
Bảng biến thiên:

Vậy có 2200 ti vi được bán ra thì lợi nhuận là cao nhất. Số ti vi mua tăng lên là: \(2200 - 1000 = 1\;200\) (chiếc)
Vậy cửa hàng nên đặt giá bán là: \(14 - 0,5.\frac{{1\;200}}{{100}} = 8\) (triệu đồng)
- LT2
- VD
Trả lời câu hỏi Luyện tập 2 trang 38 SGK Toán 12 Kết nối tri thức
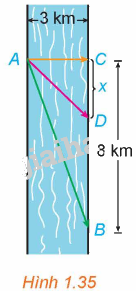
Anh An chèo thuyền từ điểm A trên bờ một con sông thẳng rộng 3km và muốn đến điểm B ở bờ đối diện cách 8km về phía hạ lưu càng nhanh càng tốt (H.1.35). Anh An có thể chèo thuyền trực tiếp qua sông đến điểm C rồi chạy bộ đến B, hoặc anh có thể chèo thuyển thẳng đến B, hoặc anh cũng có thể chèo thuyền đến một điểm D nào đó giữa C và B rồi chạy bộ đến B. Nếu vận tốc chèo thuyền là 6km/h và vận tốc chạy bộ là 8km/h thì anh An phải chèo thuyền sang bờ ở điểm nào để đến B càng sớm càng tốt? (Giả sử rằng vận tốc của nước là không đáng kể so với vận tốc chèo thuyền của anh An).
Phương pháp giải:
Sử dụng kiến thức về cách giải bài toán tối ưu hóa đơn giản để tính:
Bước 1: Xác định đại lượng Q mà ta cần làm cho giá trị của đại lượng ấy lớn nhất hoặc nhỏ nhất và biểu diễn nó qua các đại lượng khác trong bài toán.
Bước 2: Chọn một đại lượng thích hợp nào đó, kí hiệu là x, và biểu diễn các đại lượng khác ở Bước 1 theo x. Khi đó, đại lượng Q sẽ là hàm số của một biến x. Tìm tập xác định của hàm số \(Q = Q\left( x \right)\).
Bước 3: Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số \(Q = Q\left( x \right)\) bằng các phương pháp đã biết và kết luận.
Lời giải chi tiết:
Gọi độ dài đoạn CD là x (km \(0 < x < 8\))
Quãng đường AD dài: \(\sqrt {A{C^2} + D{C^2}} = \sqrt {9 + {x^2}} \left( {km} \right)\)
Quãng đường BD dài \(8 - x\left( {km} \right)\)
Thời gian người đó đi đến B bằng cách chèo thuyền đến một điểm D nào đó giữa C và B rồi chạy bộ đến B là: \(\frac{{\sqrt {9 + {x^2}} }}{6} + \frac{{8 - x}}{8}\) (giờ)
Xét hàm số \(y = \frac{{\sqrt {9 + {x^2}} }}{6} + \frac{{8 - x}}{8}\) với \(0 < x < 8\)
Ta có: \(y' = \frac{x}{{6\sqrt {9 + {x^2}} }} - \frac{1}{8}\)
\(y' = 0 \Leftrightarrow \frac{x}{{6\sqrt {9 + {x^2}} }} - \frac{1}{8} = 0 \Leftrightarrow 4x = 3\sqrt {9 + {x^2}} \Leftrightarrow \left\{ \begin{array}{l}16{x^2} = 9\left( {9 + {x^2}} \right)\\x > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} = \frac{{81}}{7}\\x > 0\end{array} \right. \Leftrightarrow x = \frac{9}{{\sqrt 7 }}\)
Bảng biến thiên:
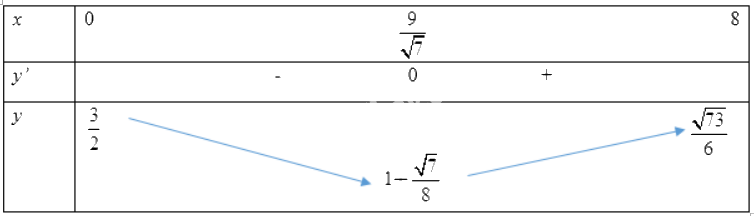
Vậy anh An phải chèo thuyền sang bờ ở điểm D cách C một khoảng bằng \(\frac{9}{{\sqrt 7 }}km\) thì đến B sớm nhất.
Trả lời câu hỏi Vận dụng trang 40 SGK Toán 12 Kết nối tri thức
Một nhà sản xuất trung bình bán được 1 000 ti vi màn hình phẳng mỗi tuần với giá 14 triệu đồng một chiếc. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 500 nghìn đồng, số lượng ti vi bán ra sẽ tăng thêm khoảng 100 ti vi mỗi tuần.
a) Tìm hàm cầu.
b) Công ty nên giảm giá bao nhiêu cho người mua để doanh thu là lớn nhất?
c) Nếu hàm chi phí hằng tuần là \(C\left( x \right) = 12\;000 - 3x\) (triệu đồng), trong đó x là số ti vi bán ra trong tuần, nhà sản xuất nên đặt giá bán như thế nào để lợi nhuận là lớn nhất?
Phương pháp giải:
a) Sử dụng kiến thức về hàm cầu để tìm hàm cầu: Gọi p(x) là giá bán mỗi đơn vị mà công ty có thể tính nếu bán x đơn vị. Khi đó, p được gọi là hàm cầu (hay hàm giá).
b) Sử dụng kiến thức về hàm doanh thu để tính: Nếu x đơn vị được bán và giá mỗi đơn vị là p(x) thì tổng doanh thu là: R(x)=x.p(x), khi đó R(x) được gọi là hàm doanh thu.
c) Nếu x đơn vị được bán thì tổng lợi nhuận là \(P\left( x \right) = R\left( x \right) - C\left( x \right)\) thì P(x) là hàm lợi nhuận và C(x) là hàm chi phí.
Sử dụng kiến thức về cách giải bài toán tối ưu hóa đơn giản để tính:
Bước 1: Xác định đại lượng Q mà ta cần làm cho giá trị của đại lượng ấy lớn nhất hoặc nhỏ nhất và biểu diễn nó qua các đại lượng khác trong bài toán.
Bước 2: Chọn một đại lượng thích hợp nào đó, kí hiệu là x, và biểu diễn các đại lượng khác ở Bước 1 theo x. Khi đó, đại lượng Q sẽ là hàm số của một biến x. Tìm tập xác định của hàm số \(Q = Q\left( x \right)\).
Bước 3: Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số \(Q = Q\left( x \right)\) bằng các phương pháp đã biết và kết luận.
Lời giải chi tiết:
a) Gọi p (triệu đồng) là giá của mỗi ti vi, x là số ti vi. Khi đó, hàm cầu là \(p = p\left( x \right)\).
Theo giả thiết, tốc độ thay đổi của x tỉ lệ với tốc độ thay đổi của p nên hàm số \(p = p\left( x \right)\) là hàm số bậc nhất nên. Do đó, \(p\left( x \right) = ax + b\) (a khác 0).
Giá tiền \({p _1} = 14\) ứng với \({x_1} = 1\;000\), giá tiền \({p_2} = 13,5\) ứng với \({x_2} = 1\;000 + 100 = 1\;100\)
Do đó, phương trình đường thẳng \(p\left( x \right) = ax + b\) đi qua hai điểm (1000; 14) và (1 100; 13,5). Ta có hệ phương trình: \(\left\{ \begin{array}{l}14 = 1\;000a + b\\13,5 = 1\;100a + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{ - 1}}{{200}}\\b = 19\end{array} \right.\) (thỏa mãn)
Vậy hàm cầu là: \(p\left( x \right) = - \frac{1}{{200}}x + 19\)
b) Vì \(p = \frac{{ - 1}}{{200}}x + 19 \Rightarrow x = - 200p + 3\;800\)
Hàm doanh thu từ tiền bán ti vi là: \(R\left( p \right) = px = p\left( { - 200p + 3\;800} \right) = - 200{p^2} + 3\;800p\)
Để doanh thu là lớn nhất thì ta cần tìm p sao cho R đạt giá trị lớn nhất.
Ta có: \(R'\left( p \right) = - 400p + 3\;800,R'\left( p \right) = 0 \Leftrightarrow p = \frac{{19}}{2}\)
Bảng biến thiên:
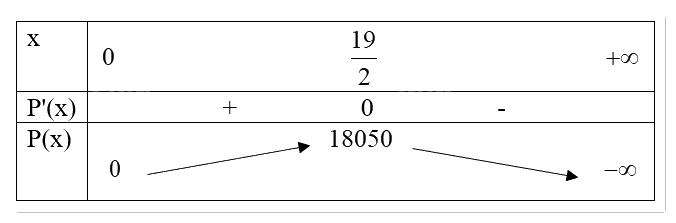
Vậy công ty nên giảm giá số tiền một chiếc ti vi là: \(14 - \frac{{19}}{2} = 4,5\) (triệu đồng) thì doanh thu là lớn nhất.
c) Doanh thu bán hàng của x sản phẩm là: \(R\left( x \right) = x.p\left( x \right) = x.\left( {\frac{{ - 1}}{{200}}x + 19} \right) = \frac{{ - {x^2}}}{{200}} + 19x\) (triệu đồng)
Do đó, hàm số thể hiện lợi nhuận thu được khi bán x sản phẩm là:
\(P\left( x \right) = R\left( x \right) - C\left( x \right) = \frac{{ - {x^2}}}{{200}} + 19x - 12\;000 + 3x = \frac{{ - {x^2}}}{{200}} + 22x - 12\;000\) (triệu đồng).
Để lợi nhuận là lớn nhất thì P(x) là lớn nhất.
Ta có: \(P'\left( x \right) = \frac{{ - x}}{{100}} + 22,P'\left( x \right) = 0 \Leftrightarrow x = 2\;200\)
Bảng biến thiên:
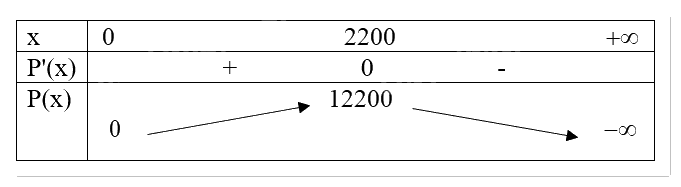
Vậy có 2200 ti vi được bán ra thì lợi nhuận là cao nhất. Số ti vi mua tăng lên là: \(2200 - 1000 = 1\;200\) (chiếc)
Vậy cửa hàng nên đặt giá bán là: \(14 - 0,5.\frac{{1\;200}}{{100}} = 8\) (triệu đồng)
Giải mục 2 trang 36, 37, 38 SGK Toán 12 tập 1 - Kết nối tri thức: Tổng quan và Hướng dẫn chi tiết
Mục 2 của SGK Toán 12 tập 1 Kết nối tri thức tập trung vào việc nghiên cứu về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng trong chương trình Toán học lớp 12, đóng vai trò then chốt trong việc hiểu các khái niệm nâng cao hơn như đạo hàm và tích phân. Việc nắm vững kiến thức về giới hạn hàm số không chỉ giúp các em giải quyết các bài tập trong SGK mà còn là bước đệm quan trọng cho các kỳ thi quan trọng như THPT Quốc gia.
Nội dung chính của Mục 2:
- Khái niệm giới hạn của hàm số tại một điểm: Hiểu rõ định nghĩa, ý nghĩa và các tính chất cơ bản của giới hạn hàm số.
- Giới hạn một bên: Phân biệt và vận dụng giới hạn trái, giới hạn phải trong các bài toán cụ thể.
- Giới hạn vô cùng: Nghiên cứu giới hạn của hàm số khi x tiến tới vô cùng hoặc trừ vô cùng.
- Các dạng giới hạn đặc biệt: Giải quyết các bài toán giới hạn có dạng vô định (0/0, ∞/∞).
Giải chi tiết các bài tập trang 36, 37, 38
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 2, trang 36, 37, 38 SGK Toán 12 tập 1 Kết nối tri thức:
Bài 1: (Trang 36)
(Đề bài)
Lời giải:
(Giải thích chi tiết từng bước, kèm theo các công thức và định lý liên quan)
Bài 2: (Trang 37)
(Đề bài)
Lời giải:
(Giải thích chi tiết từng bước, kèm theo các công thức và định lý liên quan)
Bài 3: (Trang 38)
(Đề bài)
Lời giải:
(Giải thích chi tiết từng bước, kèm theo các công thức và định lý liên quan)
Mẹo giải bài tập về giới hạn hàm số
- Nắm vững định nghĩa: Hiểu rõ định nghĩa giới hạn hàm số là chìa khóa để giải quyết mọi bài toán.
- Sử dụng các tính chất: Vận dụng linh hoạt các tính chất của giới hạn để đơn giản hóa bài toán.
- Biến đổi đại số: Thường xuyên sử dụng các phép biến đổi đại số để đưa bài toán về dạng quen thuộc.
- Áp dụng quy tắc L'Hôpital: Sử dụng quy tắc L'Hôpital khi gặp các dạng giới hạn vô định.
Tài liệu tham khảo thêm
Để hiểu sâu hơn về giới hạn hàm số, các em có thể tham khảo thêm các tài liệu sau:
- Sách giáo khoa Toán 12 tập 1 - Kết nối tri thức
- Sách bài tập Toán 12 tập 1 - Kết nối tri thức
- Các trang web học Toán trực tuyến uy tín
Tusach.vn hy vọng rằng với lời giải chi tiết và những hướng dẫn trên, các em sẽ tự tin hơn trong việc giải quyết các bài tập về giới hạn hàm số. Chúc các em học tập tốt!