Lý Thuyết Nguyên Hàm Toán 12 Kết Nối Tri Thức

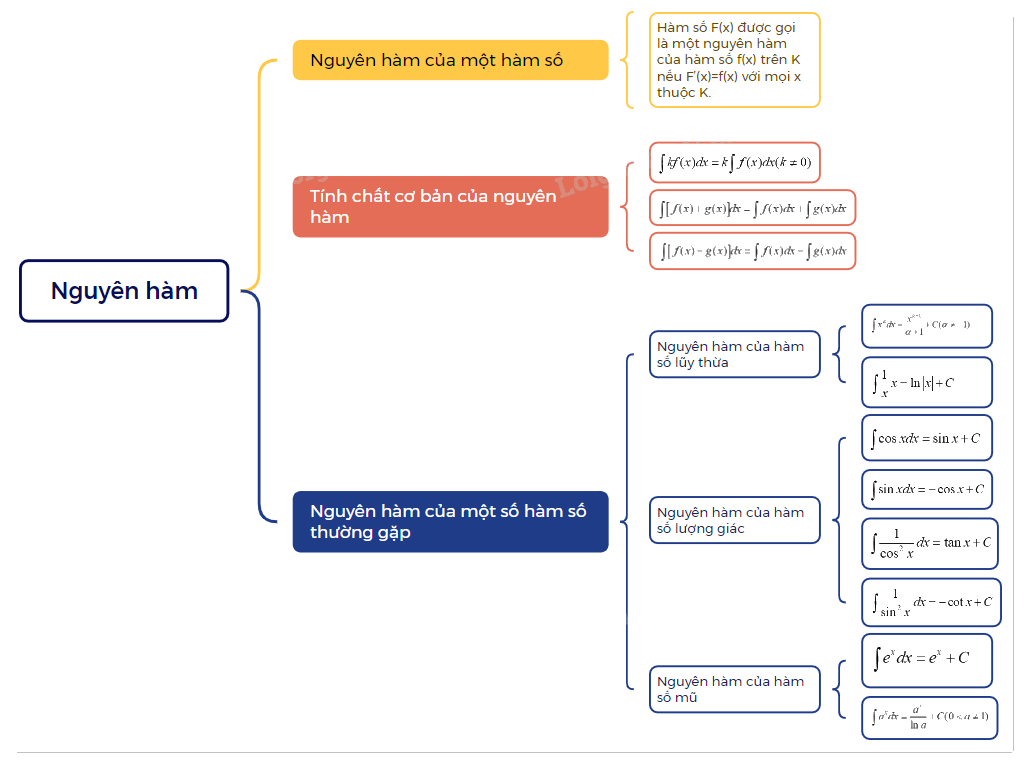
Lý thuyết Nguyên hàm Toán 12 Kết nối tri thức

Nguyên hàm là một khái niệm quan trọng trong chương trình Toán 12, đặc biệt là trong phần Tích phân. Việc nắm vững lý thuyết nguyên hàm không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng cho các kiến thức nâng cao.

Tại tusach.vn, chúng tôi cung cấp tài liệu lý thuyết nguyên hàm Toán 12 Kết Nối Tri Thức đầy đủ, chính xác và dễ hiểu, giúp bạn học tập hiệu quả.

Lý thuyết Nguyên hàm

1. Nguyên hàm của một hàm số

Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu F’(x)=f(x) với mọi x thuộc K.

Chú ý:

Giả sử hàm số F(x) là một nguyên hàm của f(x) trên K. Khi đó:

a) Với mỗi hằng số C, hàm số F(x) + C cũng là một nguyên hàm của f(x) trên K

b) Nếu hàm số G(x) là một nguyên hàm của f(x) trên K thì tồn tại một hằng số C sao chp G(x) = F(x) + C với mọi x thuộc K

Như vậy, nếu F(x) là một nguyên hàm của f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C (C là hằng số). Ta gọi F(x) + C là họ các nguyên hàm của f(x) trên K, kí hiệu bởi \(\int {f(x)dx} \).

2. Tính chất cơ bản của nguyên hàm

\(\int {kf(x)dx = k\int {f(x)dx(k \ne 0)} } \)
\(\int {\left[ {f(x) + g(x)} \right]} dx = \int {f(x)dx + \int {g(x)dx} } \)
\(\int {\left[ {f(x) - g(x)} \right]} dx = \int {f(x)dx - \int {g(x)dx} } \)

3. Nguyên hàm của một số hàm số thường gặp

a) Nguyên hàm của hàm số lũy thừa

Hàm số lũy thừa \(y = {x^\alpha }(\alpha \in R)\) có đạo hàm với mọi x > 0 và \(({x^\alpha })' = \alpha {x^{\alpha - 1}}\)

\(\int {{x^\alpha }dx = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C(\alpha \ne - 1)} \)
\(\int {\frac{1}{x}x = \ln \left| x \right| + C} \)

b) Nguyên hàm của hàm số lượng giác

\(\int {\cos xdx = \sin x + C} \)
\(\int {\sin xdx = - \cos x + C} \)
\(\int {\frac{1}{{{{\cos }^2}x}}dx = \tan x + C} \)
\(\int {\frac{1}{{{{\sin }^2}x}}dx = - \cot x + C} \)

c) Nguyên hàm của hàm số mũ

\(\int {{e^x}dx = {e^x} + C} \)
\(\int {{a^x}dx = \frac{{{a^x}}}{{\ln a}} + C(0 < a \ne 1)} \)

Lý thuyết Nguyên hàm Toán 12 Kết nối tri thức 1

Lý Thuyết Nguyên Hàm Toán 12 Kết Nối Tri Thức: Tổng Quan Chi Tiết

Nguyên hàm là một khái niệm then chốt trong chương trình Toán 12, đóng vai trò quan trọng trong việc giải quyết các bài toán tích phân. Hiểu rõ lý thuyết nguyên hàm là nền tảng để làm chủ kiến thức và đạt kết quả cao trong các kỳ thi.

1. Định Nghĩa Nguyên Hàm

Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên khoảng K nếu F'(x) = f(x) với mọi x thuộc K. Nói cách khác, đạo hàm của nguyên hàm bằng chính hàm số ban đầu.

2. Tính Chất Của Nguyên Hàm

Nếu F(x) là một nguyên hàm của f(x) thì F(x) + C cũng là một nguyên hàm của f(x), với C là một hằng số bất kỳ.
Hàm số f(x) có vô số nguyên hàm, chúng khác nhau ở hằng số cộng.

3. Các Công Thức Nguyên Hàm Cơ Bản

Dưới đây là một số công thức nguyên hàm cơ bản mà bạn cần nắm vững:

Hàm số f(x)	Nguyên hàm F(x)
xⁿ (n ≠ -1)	(xⁿ⁺¹)/(n+1) + C
1/x	ln\|x\| + C
e^x	e^x + C
sin(x)	-cos(x) + C
cos(x)	sin(x) + C

4. Phương Pháp Tìm Nguyên Hàm

Có nhiều phương pháp để tìm nguyên hàm, bao gồm:

Sử dụng bảng công thức nguyên hàm: Đây là phương pháp nhanh chóng và hiệu quả nhất khi hàm số cần tìm nguyên hàm có dạng quen thuộc.
Phương pháp đổi biến số: Phương pháp này được sử dụng khi hàm số có dạng phức tạp, có thể đưa về dạng đơn giản hơn bằng cách đổi biến.
Phương pháp tích phân từng phần: Phương pháp này được sử dụng khi hàm số là tích của hai hàm số khác.

5. Ví Dụ Minh Họa

Ví dụ 1: Tìm nguyên hàm của hàm số f(x) = 2x³ + 3x² - 1.

Giải:

Nguyên hàm của f(x) là:

F(x) = (2x⁴)/4 + (3x³)/3 - x + C = (x⁴)/2 + x³ - x + C

Ví dụ 2: Tìm nguyên hàm của hàm số f(x) = sin(2x).

Giải:

Sử dụng phương pháp đổi biến số: u = 2x, suy ra du = 2dx, hay dx = du/2.

Nguyên hàm của f(x) là:

F(x) = ∫sin(u) (du/2) = (-1/2)cos(u) + C = (-1/2)cos(2x) + C

6. Luyện Tập và Củng Cố Kiến Thức

Để nắm vững lý thuyết nguyên hàm, bạn cần luyện tập thường xuyên với các bài tập khác nhau. tusach.vn cung cấp một hệ thống bài tập đa dạng, từ cơ bản đến nâng cao, giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán.

Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và đạt kết quả tốt nhất trong môn Toán!